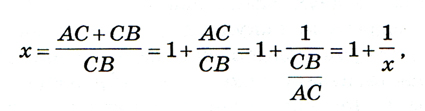Золотое сечение в прямоугольном треугольнике (8 видео)

Золотое сечение и тригонометрия

Золотое сечение и тригонометрия.

На оси координат можно построить график функции у = f Ф^ Х, где ^- корень квадратный или ; степень числа. Ф = 1,61803398. Ф^ = 1,2720196.
Число Ф можно легко посчитать по формуле. Ф = (5^ + 1)/2, где ^- корень квадратный.
Число 1/Ф = (5^ – 1)/2 = 0,618033.
График функции это прямая из начала координат и проходящую через точку с параметрами: Х = 1; У = 1,2720196. Линия графика проходит под углом
La = 51,827292 градусов.
Числа золотого сечения образуют прямоугольный треугольник. Катет В = 1,
катет А = Ф^ = 1,2720196, гипотенуза С = Ф = 1,618034 и углами La = 51,8273 в основании
пирамиды и Lв = 38,172708 при вершине треугольника. Гипотенуза С равна квадрату катета А.
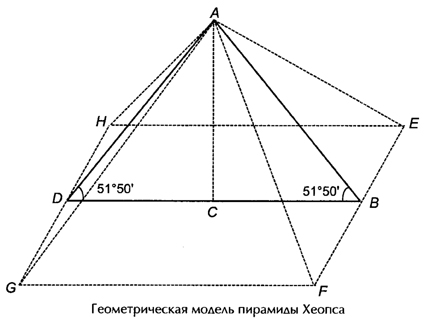
Этот треугольник является базовым для пирамиды Хеопса, в которой высота это больший катет, а меньший катет лежит на основании пирамиды, апофема пирамиды это гипотенуза прямоугольного треугольника.
Обратная величина высоты большой пирамиды равна высоте малой пирамиды.
Н = Ф^ = 1,2720196. h = 1/Ф^ = 0,7861513.
Получаем самый обыкновенный, тригонометрический, прямоугольный треугольник, с гипотенузой L= B = 1, катетом M = h = 0,78615 и катетом N = 0,618034. У этого малого треугольника угол при основании пирамиды 38,172. Угол при вершине треугольника 51,82 градуса.
Это уникальные, базовые, прямоугольные треугольники, которые удовлетворяют следующим требованиям:
Треугольники прямоугольные.
Углы треугольника 51,827292 и 38,172708.
Катет большого треугольника обратно пропорционален катету малого.
Гипотенуза большого обратно пропорциональна катету малого.
Катет большого равен гипотенузе малого и равен единице и они лежат на одной линии.
Для большого, гипотенуза равна квадрату катета.
Для малого, один катет равен квадрату второго.
Катет N обратно пропорционален числу Золотого сечения Ф, N = 1/Ф.
Ф = 1,618034 = 1/0,618034.
И самое главное условие:
Суммы высоты Н = A и обратного ей катета M образуют гипотенузу прямоугольного треугольника К = 1,2720192 + 0,7861513 = 2,058171, в котором катетами являются гипотенуза С = 1,618 033 и катет А = 1,272019 большого треугольника.
К = Ф х Н = RT = М = 1,618033 х 1,2720192 = 2,058171, где R = Ф.
Число Ф выполняет функцию радиуса R пространства.
Число К = RT = RR^ = М, выполняет функцию радиуса RT периода времени, или
М – момента импульса, где ^- корень квадратный.

Произвольный прямоугольный треугольник, даже с квадратом катета, равным гипотенузе будет иметь другие углы. Это не будет треугольник Золотого сечения.
Если все стороны базового большого треугольника увеличить на масштабный коэффициент, получим и обратно пропорциональный малый треугольник.
Таких треугольников будет множество и все они подобны базовым треугольникам Золотого сечения.
Маленькие так вообще образуют высокие гармоники основного тона.
Почему-то низких гармоник основного тона не образуется в природе, они что, повернут время вспять? Низкие гармоники можно только посчитать в попугаях.
Храм может быть очень большим, по пять рублей за квадрат, а может быть избушка на курьих ножках. Но если отношение высоты к длине основания удовлетворяет пропорциям золотой серединки, то строения выдержаны в нормах Золотого сечения.
К примеру, для рычага, длиной единица, АС =1, существует древнегреческое правило:
Точка опоры рычага делит его на плечи. Длина малого плеча АВ = 0,381966 равна квадрату большего плеча ВС = 0,618034.
Отношение большего плеча к меньшему равно отношению всей длины рычага к его большей части: ВС/АВ = АС/ВС.
А если взять масштабный коэффициент длины рычага, скажем, равным F = 2,618034, что изменится в отношениях плеч? Ничего!
Однако длина малого плеча будет равна единице, и никаких чисел меньше единицы в увеличенном рычаге не существует.
Вот так же самостийно поступает Солнце со своими вассалами, умножая все пространство вокруг себя на свой коэффициент массы. И полетели все обратно пропорциональные зависимости в тартарары.
И попробуй посчитай после этого Солнечную систему…
Да, кстати, по закону справедливости, а требовать справедливости – это диагноз, по справедливости, если что-то где-то приумножается у власти, значит, у плебса рэкетом делится.
А это наводит на мысль, что где-то в своих покоях Солнце спрятало с глаз долой тот самый уменьшившийся в размерах рычаг f = 1/F = 0,381966.
Да. Такие вот дела. Вперед, шерлоки!

Однако треугольники, подобные базовым, большой и обратный, не образуют общий треугольник с гипотенузой К, потому что на катете большого, что в основании пирамиды, не будет лежать гипотенуза маленького и они не будут равны между собой и равны единице.
Между их высотами образуется разрыв!

В принципе, начертить под верхней пирамидой нижнюю, с обратно пропорциональной высотой и вершиной вниз, не составляет труда и не надо было бы использовать столько слов пояснения.

И последнее условие:
Теперь тригонометрия Золотого сечения.
Нам понадобится калькулятор с функциями косинуса и тангенса.
Косинус угла 38,172708 градусов равен 0,7861513. соs 38,172796 = 0,7861513.
Обратная функция тангенса tg’позволяет по значению угла находить величину угла в градусах, где ‘- минус первая степень числа. tg’ 0,7861513 = 38,172796 градусов.
Это есть уникальное свойство углов базового прямоугольного треугольника Золотого сечения.
Более ни для каких углов такое соотношение не выполняется! Начальный и конечный углы будут не равны по социальному статусу.
Тема:
Если взять произвольный угол из диапазона от 1 градуса до 90 градусов, но не равный углу 38,172 градуса и начать периодически вычислять по алгоритму cosA = tg’ y = B градусов; cosB = tg’х = С гр.; cosC = tg’ z = D градусов и так далее до бесконечности.
Вычисляемые углы и их значения будут вечно стремиться к своему пределу угла 38,172 в градусах и его значению 0,7861513 и никогда его точное значение человечество не достигнет.
Число Ф = 1,618034 – число иррациональное, как и число ПИ = 3,14159.
Пример: cos 39 =tg’0,809 = 38,973; cos 38,973 = tg’0,777 = 37,86; cos 37,86 = tg 0,7894 =38,29; cos 38,29 = tg’0,78487 = 38,127; cos = 38,127 = tg’0,7866 = 38,19; cos 38,19 = tg’ит.д.

Если присмотреться к процессу, заметно, значения углов ложатся как пули, то большее справа, то меньшее слева, снова большее справа, меньшее слева. Но значения углов постепенно приближаются к своему пределу, углу Золотого сечения 38,17208… градусов.
Аналогичная ситуация и со значение углов и их пределом 0,7861513…

Что творится внизу, а что сверху дает понимание пирамида золотого сечения.
Для верхней пирамиды апофема ее – С =1,618034 и является гипотенузой,
высота Н = А = 1,2720196 — это большой катет, малый катет равен единице, В = 1.
Он лежит в основании пирамиды.
Это большой треугольник.
Для малого треугольника имеем: а = 0,7861513 – большой катет, малый катет в =0,618033, а гипотенуза стала равной единице, с =1.
Внизу все имеет свои имена, и то, что было наверху катетом, равным единице, внизу стало единичной гипотенузой.
Вот так вот! Переобуваются в воздухе, как настоящие партийцы, кто был никем, тот станет всем!
Для наглядности надо начертить под верхней пирамидой нижнюю, с обратно пропорциональной высотой и вершиной вниз.
Если сложить треугольники таким образом, что на катете большого треугольника будет лежать гипотенуза малого треугольника, мы получим внизу усеченную пирамиду с пирамидальной дыркой по высоте пирамиды, потому что катет в = 0,618034 будет составлять к основанию верхней пирамиды угол 51,827292 град.
Чтобы получить полноценную усеченную пирамиду, вовнутрь нижней пирамиды надо вставить маленькую пирамидку с его треугольником: С катетом 0,4858682, он будет высотой пирамидки и станет продолжением высоты большой пирамиды, с гипотенузой 0,618034, он будет апофемой маленькой пирамидки и катетом 0,381966, он станет в основание сечения вершины малой пирамиды.
Чтобы получить полноценную малую пирамиду нужен пирамидион на вершину.
Его треугольник: гипотенуза 0,4858682, она апофема пирамидиона, катет 0,381966 – основание, катет 0,30028310 – высота пирамидиона.
У нас получается, что нижняя пирамида какая-то составная, из трех частей.
Может и с усеченной пирамидой Хеопса дела обстоят таким же образом.
Может нет пирамидиона специально, чтобы недоросли поняли намек о сложности строения пирамиды!
Верхний и нижний треугольники образуют новый прямоугольный треугольник,
у которого гипотенуза равна 2,058171 и состоит из двух обратно пропорциональных высот
пирамид, Н + h = 1,27019 + 0,7861513, катета 1,618034 и 1,2720196.
Это апофемы, соответственно, верхней и нижней пирамид, основание пирамид общее и равно единице.

Все дело в том, что может быть много подобных друг другу пирамид. Надо умножать высоту базовой на коэффициент масштаба, а он может быть сколь угодно большим.
Высоты пирамид являются обратно пропорциональными величинами, ББВ, бесконечно большой величиной и БМВ, бесконечно малой величиной. Произведение ББВ на БМВ равно единице всегда. Их отношение всегда равно квадрату одной из них. При увеличении одной высоты в несколько раз, другая высота уменьшается во столько же раз.

Что произойдет, если высоты пирамид в базовой, единичной комплектации основания, начнут стремиться к единице обновремено?
Пирамиды станут плоским и превратятся в площадь в 1 квадратную единицу.
Мир станет абсолютно плоским.
В реальности пирамиды существуют в параллельных, зависимых и независимых мирах.
Для мира Великанов мир Лилипутов воспринимается совершенно плоским.
Трехмерные Лилипуты могут видеть мир Великанов только плоским.
Такое видение представляет из себя чертеж куба на листе бумаги. Объем куба можно представить только в воображении.
Возможно, миражи могут являться трехмерной проекцией одного мира в другом.
Площадь соприкосновения миров должна быть вне закона миров!
И только для стороннего от миров наблюдателя, для Гулливера, представлена возможность видеть оба мира в объеме одновременно.

На графике зависимости радиусов орбит планет больше единицы мира Великанов есть радиусы орбит планет мира Лилипутов.
Пояс орбит планет типа Земли, мир Лилипутов, внутренний пояс планет, и мир орбит планет гигантов, типа Юпитера-Великана, внешний пояс планет.
Объяснений такому делению системы в науке не существует.
Точка единицы графика падает на орбиту мифического Фаэтона.
Мы окунаемся в мир математических лилипутов.
Единичная окружность это общее основание двух пирамид, верхней и нижней.
Как новогодний костер для двенадцати месяцев. Все вместе и все равны.
Окружность характеризуется тем, что тангенциальная скорость равна угловой и ускорению, радиус орбиты и радиус периода равны и все составляющие элементы закона равны единице.
Все равно единице, все длится единицу. Так говорили древние и мудрые предтечи.
И то, что находится до единицы коренным образом отличается от того, что больше единицы.

Но есть одна проблема.
Единичная окружность Солнца не равна единичной окружности Юпитера.
Массы у них разные, а именно масса является коэффициентом масштабирования пространства и единица уже не единица, а положительная величина, больше единицы и то, что внизу было меньше единицы, теперь стало пропорционально больше единицы и не стало обратно пропорциональных величин.
У Земли свой масштабный коэффициент, и в его значение внесла свою лепту Луна, еще больше усугубив ситуацию с вычислениями.
И пыхтеть нам и далее на паровозе, бороздя вселенную и подбрасывая лопатой уран в топку…
Если не появится, как миссия, обновленный Шерлок Холмс.

Содержание

Исследование золотых фигур
История золотого сечения.
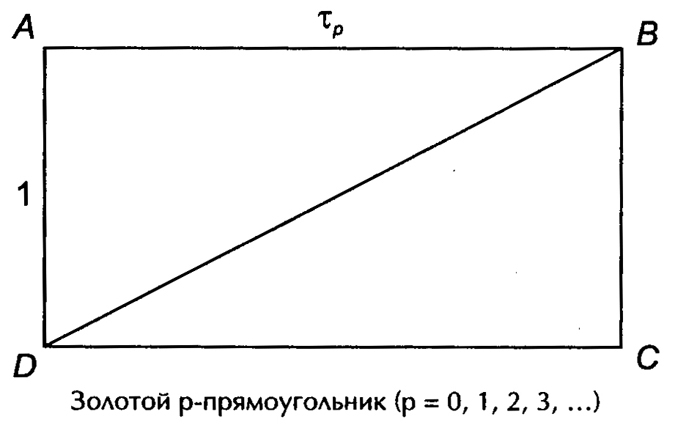
ЗОЛОТОЙ ПРЯМОУГОЛЬНИК.
ЗОЛОТОЙ ТРЕУГОЛЬНИК И ЕГО ИССЛЕДОВАНИЕ.
Применение золотого треугольника при решении задач.
ЗОЛОТАЯ ПИРАМИДА И ЕЕ ИССЛЕДОВАНИЕ.
Исследование золотой пирамиды.
Применение золотой пирамиды при решении задач.
Золотое сечение в картине Леонардо да Винчи «Джоконда»
Золотая спираль в картине Рафаэля «Избиение младенцев»
Золотое сечение
📸 Видео

Видео:Что такое золотое сечение? | Математика | TutorOnlineСкачать

Исследование золотых фигур

Разделы: Математика

«Хороший учитель обязан понимать, что никакую задачу нельзя исчерпать до конца. Этот взгляд он должен прививать и своим ученикам».
Д. Пойа

В жизни каждого человека присутствует математика. Она используется в самых разнообразных профессиях – математика нужна инженеру, военному, биологу, художнику, можно сказать, что она нужна всем. Великий художник Леонардо да Винчи был один из тех, кто заинтересовался знаменитым золотым сечением. Он много внимания уделял изучению золотого деления. Производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении; поэтому он дал этому делению название золотое сечение.

Золотое сечение интересно тем, что оно позволяет показать связь математики с другими науками, с искусством. А также помогает исследовать золотой треугольник и золотую пирамиду; рассмотреть геометрические задачи, связанные с золотыми фигурами.

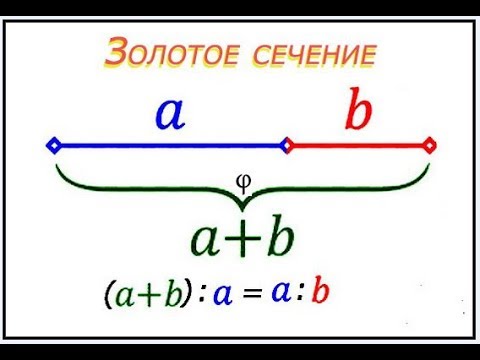
Золотое сечение – это деление отрезка на две части. Таким образом, что большая его часть относится к меньшей части как весь отрезок относится к большой части.

Рис. 1.

= или , откуда

Иногда золотым сечением называют отношение, к , которое обозначают буквой φ:

Число, обратное φ обозначают Ф:

Ф=

Отметим некоторые равенства, связывающие Ф и φ , которые нам впоследствии пригодятся:

1-Ф, 1+Ф=

История золотого сечения.

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамсеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.

В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др.. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне и они были известны только посвященным.

Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение). Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».

ЗОЛОТОЙ ПРЯМОУГОЛЬНИК.

Если построить квадрат со стороной АВ=а, найти середину М отрезка АВ и провести дугу окружности радиусом МС с центром в точке М до пересечения с продолжением стороны АВ в точке Е, то точка В разделит отрезок АЕ в крайнем и среднем отношении.

Чтобы убедиться в этом, заметим, что по теореме Пифагора

Прямоугольник АЕFD со сторонами АЕ=φАD называется золотым прямоугольником. Четырехугольник АВСD − квадрат. Нетрудно видеть, что прямоугольник ВЕFС также золотой, поскольку BC=a=φВЕ. Это обстоятельство сразу наводит на мысль о дальнейшем разбиении прямоугольника ВЕFС.

Можно ли считать, что прямоугольник с отношением сторон, равным φ, выглядит изящнее, чем прямоугольники с отношением сторон, скажем, 2:1, 3:2 или 5:7? Чтобы ответить на этот вопрос, были проведены специальные эксперименты. Результаты их не вполне убедительны, но все же свидетельствуют о некотором предпочтении, отдаваемом золотому сечению.

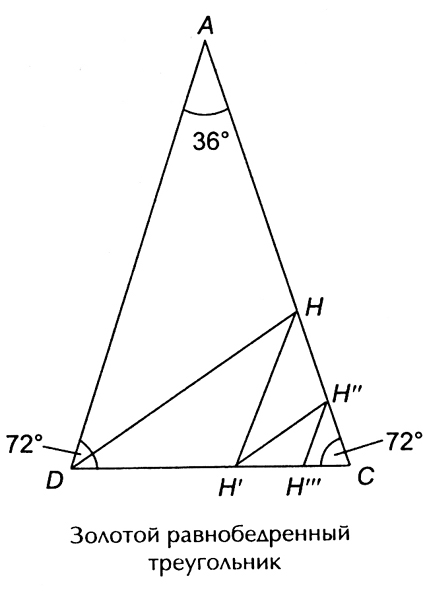
ЗОЛОТОЙ ТРЕУГОЛЬНИК И ЕГО ИССЛЕДОВАНИЕ.

Золотым треугольником будем называть равнобедренный треугольник, отношение основания которого к боковой стороне равно φ Одним из таких треугольников является треугольник с боковой стороной Ф и основанием 1; именно его мы в дальнейшем будем называть золотым. Проведем исследование золотого треугольника.

Углы золотого треугольника.

В треугольнике АВС выберем на стороне ВС точку D так, чтобы АD=1 (такую точку легко построить, проведя окружность с центром в точке А и радиусом АС). Из подобия треугольников АВС и АDС получаем:

или , откуда DС=

Поскольку ВС=Ф, DС=φ, то, учитывая равенство Ф=, получаем, что BD=1 и треугольник ABD равнобедренный. Значит, АD- биссектриса треугольника АВС. Теперь легко найти углы треугольника АВС:

5,

В последствии нам встретятся выражения, содержащие и , поэтому вычислим их значения и для удобства выразим через Ф:

=.

Найдем в золотом треугольнике:

медиану, проведенную к боковой стороне;
высоту, проведенную к основанию;
площадь;
высоту, проведенную к боковой стороне;

Пусть треугольник АВС − золотой. Для нахождения медианы воспользуемся формулой ,

где

Найдем высоту ВН: ВН=Ф

Площадь треугольника АВС будет равна: S=

Пусть – высота, проведенная к стороне ВС. Возьмем на стороне ВС точку так, чтобы . Треугольники АС и АВС подобны с коэффициентом подобия Ф, поэтому

Применение золотого треугольника при решении задач.

Найти длины диагоналей правильного 10-угольника со стороной, равной 1.

Решение. Правильный 10-угольник имеет 4 вида диагоналей, на рисунке показано по одному представителю этих четырех множеств. Найдем их длины. Проще всего найти длину отрезка AF. Для этого найдем величину внутреннего угла правильного 10-угольника: . Теперь легко заметить, что 10-угольник состоит из 10 золотых треугольников, которые имеют общую вершину О ─ центр 10-угольника. Значит, длина диагонали AF равна 2Ф.

Найдем длину диагонали АС. Из треугольника АВС имеем:

= 22) =2(1+)= 4= 2+Ф,

откуда АС=

Найдем длину диагонали AD. В равнобоковой трапеции АВСD углы при основании равны Нетрудно получить, что проекции отрезков АВ и СD на основании AD будут равны .

AD=.

Длину диагонали АЕ можно найти разными способами.

Способ 1. Будем искать ее из треугольника AEF. В этом треугольнике медиана ЕО равна половине стороны AF, поэтому треугольник AEF-прямоугольный. Тогда АЕ= AF

Способ 2. Заметим, что высота золотого треугольника EOF является средней линией треугольника AEF. Поскольку эта высота равна , то АЕ=

Ответ: 2Ф, ,

ЗОЛОТАЯ ПИРАМИДА И ЕЕ ИССЛЕДОВАНИЕ.

Пирамида называется золотой, если каждая её грань − золотой треугольник.

Исследование золотой пирамиды.

Различные способы нахождения объёма золотой пирамиды.

I способ: объем пирамиды находим по формуле . Для этого нам необходимо вычислить высоту пирамиды.

Пусть DABC-данная пирамида,DH − ее высота. Плоскость ADH пересекает ребро ВС в точке М, причем ВМ=СМ. Треугольник ADM − равнобедренный.

Опустим на его основание AD высоту МК. Из подобия треугольников AHD и AKM будем иметь:

.

Поставим в это равенство известные нам числа:

МК= (расстояние между ребрами AD и ВС),

АМ= (высота золотого треугольника):

DH=. А т.к. =.

II способ:

длины противоположных ребер, расстояние между ними, – угол между ними;

III способ:

Объем золотой пирамиды – это объем прямоугольного параллелепипеда минус объем четырех маленьких пирамид с ребрами длиной 1,, и , значит:

Применение золотой пирамиды при решении задач.

Найдем площадь поверхности золотой пирамиды.

= = 4

Золотое сечение в картине Леонардо да Винчи «Джоконда»

Портрет Моны Лизы привлекает тем, что композиция рисунка построена на»золотых треугольниках» (точнее на треугольниках, являющихся кусками правильного звездчатого пятиугольника).

Золотая спираль в картине Рафаэля «Избиение младенцев»

В отличии от золотого сечения ощущение динамики, волнения проявляется, пожалуй, сильней всего в другой простой геометрической фигуре – спирали. Многофигурная композиция, выполненная в 1509 – 1510 годах Рафаэлем, когда прославленный живописец создавал свои фрески в Ватикане, как раз отличается динамизмом и драматизмом сюжета. Рафаэль так и не довел свой замысел до завершения, однако, его эскиз был гравирован неизвестным итальянским графиком Маркантинио Раймонди, который на основе этого эскиза и создал гравюру» Избиение младенцев». На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции −точки, где пальцы воина сомкнулись вокруг лодыжки ребенка, − вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Если естественным образом соединить эти куски кривой пунктиром, то с очень большой точностью получается . золотая спираль! Это можно проверить, измеряя отношение длин отрезков, высекаемых спиралью на прямых, проходящих через начало кривой.

Мы не знаем, рисовал ли на самом деле Рафаэль золотую спираль при создании композиции » Избиение младенцев» или только»чувствовал» её. Однако с уверенностью можно сказать, что гравер Раймонди эту спираль увидел.

Об этом свидетельствуют добавленные им новые элементы композиции, подчеркивающие разворот спирали в тех местах, где она у нас обозначена лишь пунктиром. Эти элементы можно увидеть на окончательной гравюре Раймонди: арка моста, идущая от головы женщины, − в левой части композиции и лежащее тело ребенка − в ее центре.

Нельзя не увидеть золотой треугольник и золотую пирамиду в ограненных драгоценных камнях. Многие гранильщики стараются придать бриллиантам форму тетраэдра, куба, октаэдра или икосаэдра. Но эти замечательные тела еще и потому красивы, что в основе их пропорциональных линий лежит золотая пропорция. Многие материалы, и не только драгоценные камни, состоят из мельчайших частиц, которые имеют форму многогранника. Такие вещества называются кристаллами. Соль, лед, песок, графит и т. д. состоят из кристаллов. Внутреннее устройство кристалла представляется в виде кристаллической решетки, в ячейках которых размещены по законам симметрии одинаковые мельчайшие частицы.

Литература:

Большая Российская энциклопедия. М., «Научное издательство», 2007.
Т. Каменева, А. Козлов. Золотой треугольник в задачах. М., 2007.
Журнал «Математика в школе», 1993, № 3.
Ковалев Ф.В. Золотое сечение в живописи. К.: Высшая школа, 1989.
«Математика – Энциклопедия для детей» М.: Аванта +, 1998.
Волошинов А.В. «Математика и искусство». М.: Мир, 1979.

Видео:Золотое сечение и квадратная рамаСкачать

Золотое сечение

Главная → Статьи → Золотое сечение

Весь наш мир можно описать числами. Многие числа играют настолько значительную роль в этом описании, что имеют собственные имена: Пи, экспанента (е) и т.д. Среди этих «именных» чисел есть весьма замечательное. Математики, художники, архитекторы в разные времена называли его «золотое число», «божественное число», «божественное сечение». Термин «золотое сечение» придумал Клавдий Птолемей, а популярным он стал благодаря Леонардо Да Винчи, который широко использовал его в своих работах. Люди искусства заметили, что пропорции форм, которые особенно приятны глазу для восприятия, в основе своей имеют «золотое сечение».

***
Известнейшим математическим сочинением античной науки являются «Начала» Евклида. Именно из «Начал» к нам пришла геометрическая задача «о делении отрезка в крайнем и среднем отношении». Что и является самим «Золотым сечением».
Суть задачи такова:
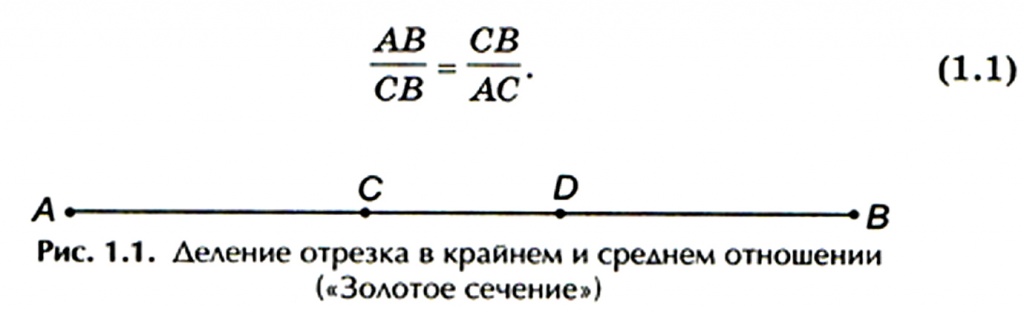
Разделим отрезок АВ точкой С в таком отношении, чтобы большая часть отрезка СВ так относилась к меньшей части отрезка АС, как отрезок АВ к своей большей части СВ, т. е.

Обозначим пропорцию (1.1) через х. Тогда, учитывая, что АВ = АС + СВ, пропорцию (1.1) можно записать в следующем виде:

откуда вытекает следующее алгебраическое уравнение для вычисления искомой пропорции х:

х* = х + 1. (1.2)
x* — в квадрате

Из «физического смысла» пропорции (1.1) вытекает, что искомое решение уравнения (1.2) должно быть положительным числом, откуда вытекает, что решением задачи о делении отрезка в крайнем и среднем отношении является положительный корень уравнения (1.2), который мы обозначим через , то есть

Приближенное значение золотой пропорции равно:
= 1,61803 39887 49894 84820 45868 34365 63811 77203…

ЗОЛОТЫЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ

На основе вышеизложенных пропорций в геометрии определены такие понятия золотых геометрических фигур:
— золотой прямоугольник (в котором отношение большей стороны к меньшей равно золотой пропорции);
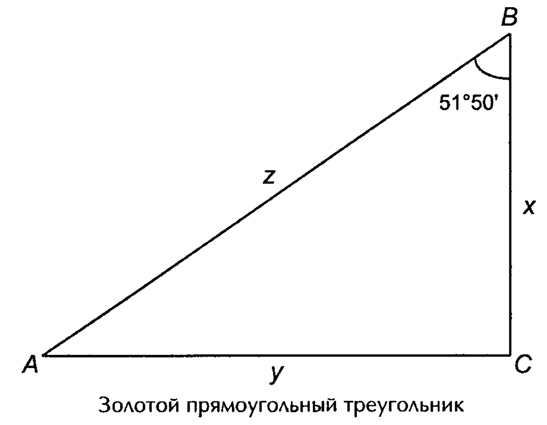
— золотой прямоугольный треугольник;
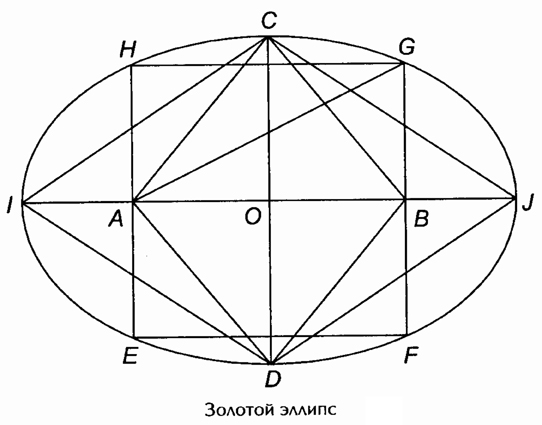
— золотой эллипс;
— золотой равнобедренный треугольник.

Прямоугольный треугольник со сторонами 3:4:5 называется «совершенным», «священным» или «египетским».
Создатели египетских пирамид выбрали в качестве «главной геометрической идеи» для пирамиды Хеопса – золотой прямоугольный треугольник, а для пирамиды Хефрена – «священный» треугольник.

Пентагон («pentagonon» — греч.), правильный пятиугольник. Если в пентагоне провести все диагонали, то в результате мы получим пятиугольную звезду, называемую пентаграммой («pentagrammon» — греч.: «pente» — пять и «grammon» — линия) или пентаклом.

Пентаграмма, называемая в народных поверьях «ведьминой стопой», играла большую роль во всех магических науках и рассматривалась как средство защиты от злых духов.
Каждые восемь лет планета Венера описывает абсолютно правильный пентакл по большому кругу небесной сферы.
Здание «Пентагона», военного ведомства США имеет форму пентагона.

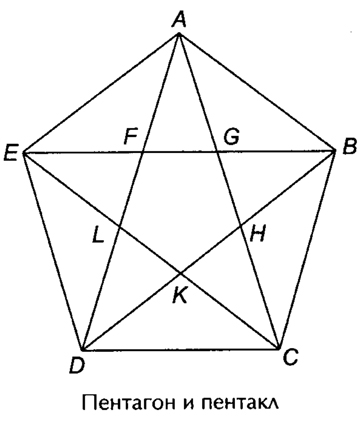
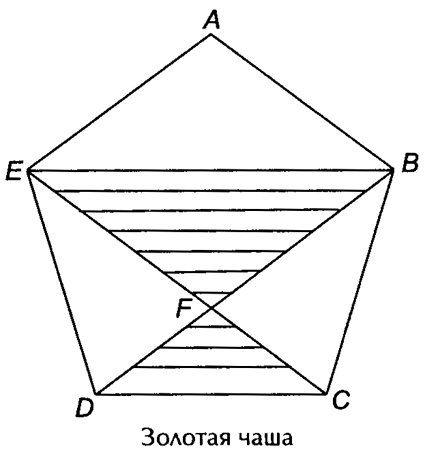
Пентагон и пентакл включают в себя ряд замечательных фигур, которые широко использовались в произведениях искусства. В античном искусстве широко известен так называемый закон золотой чаши, которые использовали античные скульпторы и золотых дел мастера. Заштрихованная часть пентагона дает схематическое представление золотой чаши.

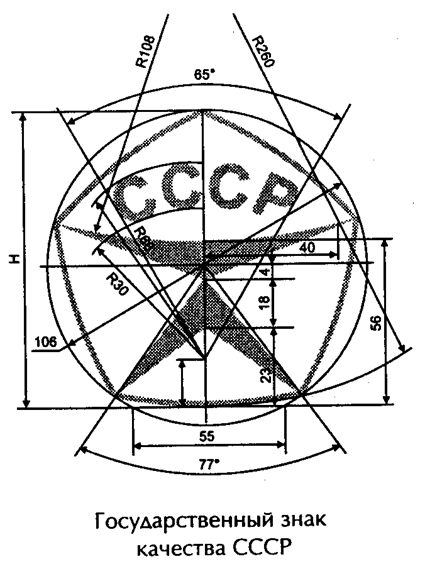
Когда-то в Советском Союзе существовал Государственный знак качества, в котором явно просматриваются мотивы золотой чаши.

В живой природе широко распространены формы, основанные на пентагональной симметрии – морские звезды, морские ежи, цветы..

ГАРМОНИЯ ЗОЛОТОГО СЕЧЕНИЯ
(краткий обзор истории искусства)

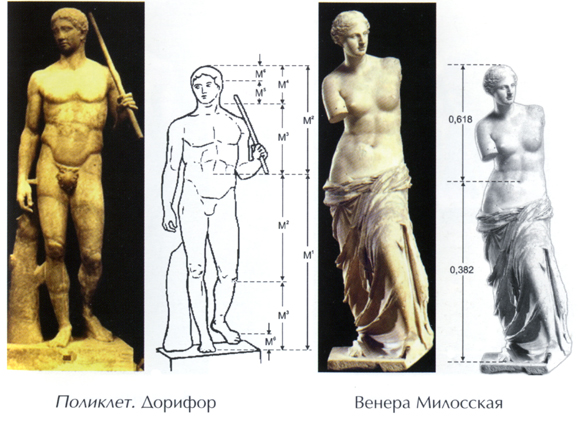
Эталоном красоты человеческого тела, образцом гармонического телосложения издав-на и по праву считаются великие творения греческих скульпторов: Фидия, Поликтета, Мирона, Праксителя. В своих творениях греческие мастера использовали принцип золотой пропорции. Одним из высших достижений классического греческого искусства может служить статуя Дорифора, изваянная Поликтетом в V веке до н. э. Эта статуя считается наилучшим примером для анализа пропорций идеального человеческого тела, установленных античными греческими скульпторами, и напрямую связана с Золотым сечение. М=0,618…
Венера Милосская, статуя богини Афродиты и эталон женской красоты, является од-ним из лучших памятников греческого скульптурного искусства.

Леонардо Да Винчи использовал пропорции Золотого сечения во многих своих самых знаменитых произведениях, и в частности, в «Тайной вечере» и знаменитой «Джоконде».
Исследователи картины «Джоконда» обнаружили, что композиционное построение кар-тины основано на двух золотых треугольниках, повернутых друг к другу своими основаниями. Гармонический анализ картины показывает, что зрачок левого глаза, через который проходит вертикальная ось полотна, находится на пересечении двух биссектрис верхнего золотого треугольника, которые с одной стороны, делят пополам углы при основании золотого треугольника, а с другой стороны, в точках пересечения с бедрами золотого треугольника делят их в пропорции Золотого сечения. Таким образом, Леонардо Да Винчи использовал в своей картине не только принцип симметрии, но и Золотое сечение.

Картина «Святое семейство» Микеланджело признана одним из шедевров западноевропейского искусства эпохи Возрождения. Гармонический анализ показал, что композиция картины основана на пентакле.

Пропорции статуи Давида (работы Микеланджело) основаны на Золотом сечении.

Яркий пример архитектуры барокко, Смольный собор в Санкт-Петербурге, производит неизгладимое впечатление. В его основных пропорциях так же усматривается Золотое сечение.

На знаменитой картине Ивана Шишкина «Корабельная роща» просматриваются мотивы Золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит картину Золотым сечением по горизонтали. Справа от сосны – освещенный солнцем при-горок. Он делит картину Золотым сечением по вертикали. Слева от главной сосны находится много сосен – можно продолжить деление Золотым сечением по горизонтали левой части картины. Наличие в картине ярких вертикалей и горизонталей, делящих ее в отношении Золотого сечения, придает ей характер уравновешенности и спокойствия.

Строительство штаб-квартиры ООН в Нью-Йорке было завершено в 1943 году. Здание привлекло тогда всеобщее внимание не только как общественное сооружение, созданное с применением новейших архитектурных средств, но и как первый пример использования сплошного солнцемодулирущего экрана на одном из фасадов. В этом здании также просматриваются мотивы Золотого сечения. В композиции здания четко выделяются три поставленных друг на друга золотых прямоугольника, которые и являются его главной архитектурной идеей.

Любое музыкальное произведение имеет временное протяжение и делится некоторыми «эстетическими вехами» на отдельные части, которые обращают на себя внимание и облегчают восприятие в целом. Этими вехами могут быть динамические и интонационные кульминационные пункты музыкального произведения. Отдельные временные интервалы музыкального произведения, соединяемые «кульминационным событием», как правило, находятся в соотношении Золотого сечения. В музыкальных произведениях различных композиторов обычно констатируется не одно Золотое сечение, а целая серия подобных сечений. Наибольшее количество произведений, в которых имеется Золоте сечение, у Аренского (95%), Бетховена (97%), Гайдна (97%), Моцарта (91%), Скрябина (90%), Шопена (92%), Шуберта (91%).

Если музыка – гармоническое упорядочение звуков, то поэзия – гармоническое упорядочение речи. Четкий ритм, закономерное чередование ударных и безударных слогов, упорядоченная размерность стихотворений, их эмоциональная насыщенность делают поэзию родной сестрой музыкальных произведений. Золотое сечение в поэзии в первую очередь проявляется как наличие определенного момента стихотворения (кульминации, смыслового перелома, главной мысли произведения) в строке, приходящейся на точку деления общего числа строк стихотворения в золотой пропорции. Так, если стихотворение содержит 100 строк, то первая точка Золотого сечения приходится на 62-ю строку (62%), вторая – на 38-ю (38%) и т. д. Произведения Александра Сергеевича Пушкина, и в том числе «Евгений Онегин» — тончайшее соответствие золотой пропорции! Произведения Шота Руставели и М.Ю. Лермонтова также построены по принципу Золотого сечения.

Один из современных видов искусства – кинематограф, — вобравший в себя драматургию действия, живопись, музыку. В выдающихся произведениях киноискусства право-мерно искать проявления Золотого сечения. Первым это сделал создатель шедевра мирового кино «Броненосец «Потемкин» кинорежиссер Сергей Эйзенштейн. В построении этой картины он сумел воплотить основной принцип гармонии – Золотое сечение. Как отмечает сам Эйзенштейн, красный флаг на мачте восставшего броненосца (точка апогея фильма) взвивается в точке золотой пропорции, отсчитываемой от конца фильма.

В течение многих тысячелетий Золотое сечение было объектом восхищения и поклонения выдающихся ученых и мыслителей: Пифагора, Платона, Евклида, Луки Пачоли, Иоганна Кеплера, Павла Флоренского…
В настоящее время Золотое сечение оказывается источником новых плодотворных идей в математике и теоретической физике, биологии и ботанике, экономике и компьютерной науке…

Материал сформирован по книге «Код да Винчи и ряды Фибоначчи» А. Стахова, А. Слученковой, И. Щербакова, 2007 года выпуска, издательства «Питер».