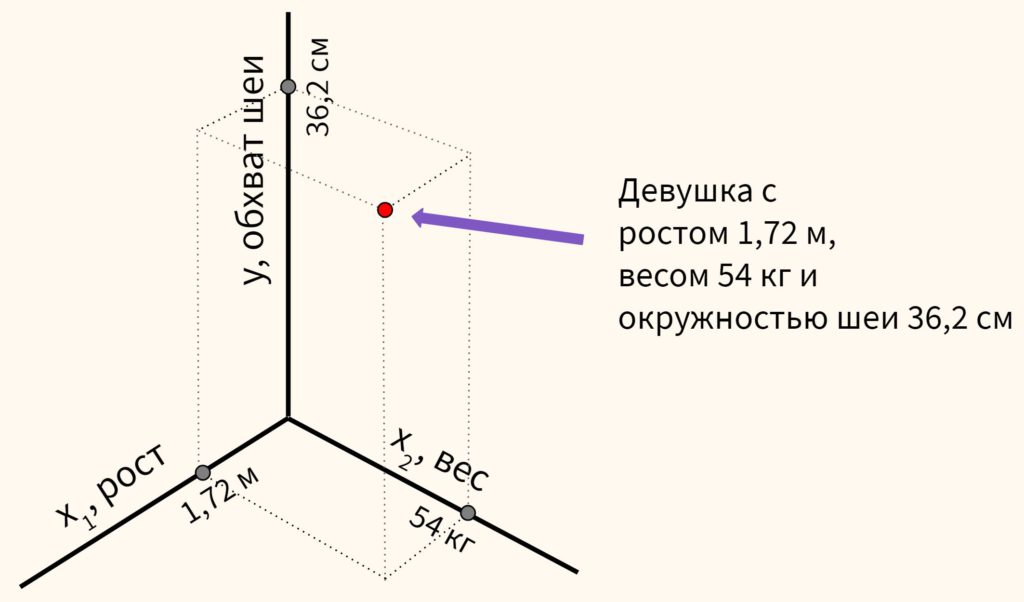
Косинусная близость векторов numpy (4 видео)

Векторы и матрицы

Ещё на первом занятии мы упомянули, что в уравнении может быть несколько независимых переменных.

$$y = w_1 times x_1 + w_2 times x_2 + e$$

Такое уравнение нельзя изобразить на координатной плоскости (имеющей два измерения, x и y), потому что в нем три переменных, а значит три измерения. Нужен график, имеющий три плоскости.

С помощью этого графика мы можем представить зависимость обхвата шеи не только от роста, но и, например, от веса.

На самом деле измерений может быть и больше, просто так как мы живём в трёхмерном пространстве, представить четыре и более измерений мы не можем. Математически же это вполне возможно.

Содержание

Данные как векторы и матрицы
Умножение векторов
Скалярное произведение векторов на Питоне
abezpalov / distance_cosine.py
Косинусное сходство в Python
Используйте модуль scipy для вычисления косинусного сходства между двумя списками в Python
Используйте модуль NumPy для вычисления косинусного сходства между двумя списками в Python
Используйте модуль sklearn для вычисления косинусного сходства между двумя списками в Python
Используйте модуль torch для вычисления косинусного сходства между двумя списками в Python
📹 Видео

Данные как векторы и матрицы

Помимо того, что мы можем представить данные на графике (по крайней мере вплоть до третьего измерения), мы также можем представить их в форме вектора. Вектор, по сути, это набор чисел, описывающих координаты наших данных.

Если взять несколько точек и соответственно несколько векторов,

то получится набор чисел, называемых матрицей.

Из сказанного выше очевидно, что любой вектор — не что иное как матрица, в которой один столбец или одна строка.

Область математики, изучающая векторы и матрицы, называется линейной алгеброй.

На этом занятии мы рассмотрим два аспекта векторных и матричных вычислений. Во-первых, посмотрим на удобный способ умножения одного вектора на другой. Во-вторых, посмотрим как мы можем рассчитать угол между двумя векторами.

Умножение векторов

Вспомним, как мы делали прогноз с помощью нашей модели. Мы умножали вес (наклон) на значение независимой переменной и прибавляли ошибку (сдвиг). Когда у нас несколько независимых переменных и несколько весов, нам нужно их попарно перемножить и сложить произведения.

Если представить и значения независимых переменных, и веса с помощью векторов, то можно воспользоваться инструментом, который называется скалярным произведением векторов (dot product), чтобы получить прогнозное

Скалярное произведение векторов на Питоне

На Питоне это реализовано с помощью библиотеки Numpy. До сих пор мы создавали массивы Numpy в, скажем так, служебных целях, чтобы использовать их, например, в моделях Scikit-learn.

Сегодня рассмотрим эти массивы сами по себе. По сути, массив Numpy (Numpy array), это и есть вектор или матрица. Давайте посмотрим, как создать такой массив, и как перемножить два вектора.

Вначале разберемся с основами работы с массивами.

Видео:#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy урокиСкачать

abezpalov / distance_cosine.py

This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters

import numpy as np

import scipy . spatial . distance as ds

vector_1 = np . array ([ 0 , 1 , 1 , 0 ])

vector_2 = np . array ([ 0 , 1 , 0 , 0 ])

dis = ds . cosine ( vector_1 , vector_2 )

You can’t perform that action at this time.

You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session.

Видео:Семинар 3 - Косинусное расстояние и близостьСкачать

Косинусное сходство в Python

Сходство косинуса измеряет сходство между списками векторов путем вычисления угла косинуса между двумя списками векторов. Если вы рассматриваете функцию косинуса, ее значение при 0 градусах равно 1 и -1 при 180 градусах. Это означает, что для двух перекрывающихся векторов значение косинуса будет максимальным и минимальным для двух точно противоположных векторов.

В этой статье мы рассчитаем косинусное сходство между двумя списками одинакового размера.

Видео:Основы NumPy Python | Массивы, Матрицы И Операции Над НимиСкачать

Используйте модуль scipy для вычисления косинусного сходства между двумя списками в Python

Функция spatial.cosine.distance() из модуля scipy вычисляет расстояние вместо косинусного подобия, но для этого мы можем вычесть значение расстояния из 1.

Видео:#6. Объединение и разделение массивов | NumPy урокиСкачать

Используйте модуль NumPy для вычисления косинусного сходства между двумя списками в Python

Функция numpy.dot() вычисляет скалярное произведение двух векторов, переданных в качестве параметров. Функция numpy.norm() возвращает векторную норму.

Мы можем использовать эти функции с правильной формулой для вычисления косинусного подобия.

Если есть несколько или список векторов и вектор запроса для вычисления косинусного сходства, мы можем использовать следующий код.

Видео:Рассчитываем контекстную близость слов с помощью библиотеки Word2vecСкачать

Используйте модуль sklearn для вычисления косинусного сходства между двумя списками в Python

В модуле sklearn есть встроенная функция под названием cosine_similarity() для вычисления косинусного сходства.

Видео:Косинусное сходство (расстояние) в Python. Cosine Similarity in Python. #python , #pythoncodeСкачать

Используйте модуль torch для вычисления косинусного сходства между двумя списками в Python

Когда мы имеем дело с N-мерными тензорами, имеющими формы (m, n), мы можем использовать функцию consine_similarity() из модуля torch , чтобы найти косинусное подобие.