Знаки тригонометрических функций по четвертям окружности (6 видео)

Знаки тригонометрических функций

Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент. В прошлый раз мы учились переводить аргументы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а затем определять эту самую координатную четверть. Теперь займемся, собственно, определением знака синуса, косинуса и тангенса.

угла α — это ордината (координата y ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.

угла α — это абсцисса (координата x ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.

угла α — это отношение синуса к косинусу. Или, что то же самое, отношение координаты y к координате x .

Обозначение: sin α = y ; cos α = x ; tg α = y : x .

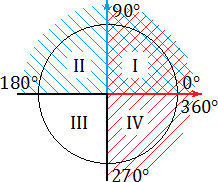
Все эти определения знакомы вам из курса алгебры старших классов. Однако нас интересуют не сами определения, а следствия, которые возникают на тригонометрической окружности. Взгляните:

Синим цветом обозначено положительное направление оси OY (ось ординат), красным — положительное направление оси OX (ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными. В частности:

sin α > 0, если угол α лежит в I или II координатной четверти. Это происходит из-за того, что по определению синус — это ордината (координата y ). А координата y будет положительной именно в I и II координатных четвертях;
cos α > 0, если угол α лежит в I или IV координатной четверти. Потому что только там координата x (она же — абсцисса) будет больше нуля;
tg α > 0, если угол α лежит в I или III координатной четверти. Это следует из определения: ведь tg α = y : x , поэтому он положителен лишь там, где знаки x и y совпадают. Это происходит в I координатной четверти (здесь x > 0, y > 0) и III координатной четверти ( x y II координатной четверти. Но синус во II четверти положителен, поэтому sin (3π/4) > 0;
cos (7π/6) = cos (7 · 180°/6) = cos 210°. Т.к. 210° ∈ [180°; 270°], это угол из III координатной четверти, в которой все косинусы отрицательны. Следовательно, cos (7π/6) IV четверти, где тангенс принимает отрицательные значения. Поэтому tg (5π/3) II четверть, в которой синусы положительны, т.е. sin (3π/4) > 0. Теперь работаем с косинусом: 150° ∈ [90°; 180°] — снова II четверть, косинусы там отрицательны. Поэтому cos (5π/6) II координатная четверть, поэтому cos (2π/3) I четверть (самый обычный угол в тригонометрии). Тангенс там положителен, поэтому tg (π/4) > 0. Опять получили произведение, в котором множители разных знаков. Поскольку «минус на плюс дает минус», имеем: cos (2π/3) · tg (π/4) II координатной четверти, где синусы положительны. Следовательно, sin (5π/6) > 0. Аналогично, 315° ∈ [270°; 360°] — это IV координатная четверть, косинусы там положительны. Поэтому cos (7π/4) > 0. Получили произведение двух положительных чисел — такое выражение всегда положительно. Заключаем: sin (5π/6) · cos (7π/4) > 0;
tg (3π/4) · cos (5π/3) = tg (3 · 180°/4) · cos (5 · 180°/3) = tg 135° · cos 300°. Но угол 135° ∈ [90°; 180°] — это II четверть, т.е. tg (3π/4) IV четверть, т.е. cos (5π/3) > 0. Поскольку «минус на плюс дает знак минус», имеем: tg (3π/4) · cos (5π/3) III координатная четверть, поэтому ctg (4π/3) > 0. Аналогично, для тангенса имеем: 30° ∈ [0; 90°] — это I координатная четверть, т.е. самый простой угол. Поэтому tg (π/6) > 0. Снова получили два положительных выражения — их произведение тоже будет положительным. Поэтому ctg (4π/3) · tg (π/6) > 0.

В заключение рассмотрим несколько более сложных задач. Помимо выяснения знака тригонометрической функции, здесь придется немного посчитать — именно так, как это делается в настоящих задачах B11. В принципе, это почти настоящие задачи, которые действительно встречается в ЕГЭ по математике.

Задача. Найдите sin α, если sin 2 α = 0,64 и α ∈ [π/2; π].

Поскольку sin 2 α = 0,64, имеем: sin α = ±0,8. Осталось решить: плюс или минус? По условию, угол α ∈ [π/2; π] — это II координатная четверть, где все синусы положительны. Следовательно, sin α = 0,8 — неопределенность со знаками устранена.

Задача. Найдите cos α, если cos 2 α = 0,04 и α ∈ [π; 3π/2].

Действуем аналогично, т.е. извлекаем квадратный корень: cos 2 α = 0,04 ⇒ cos α = ±0,2. По условию, угол α ∈ [π; 3π/2], т.е. речь идет о III координатной четверти. Там все косинусы отрицательны, поэтому cos α = −0,2.

Задача. Найдите sin α, если sin 2 α = 0,25 и α ∈ [3π/2; 2π].

Имеем: sin 2 α = 0,25 ⇒ sin α = ±0,5. Снова смотрим на угол: α ∈ [3π/2; 2π] — это IV координатная четверть, в которой, как известно, синус будет отрицательным. Таким образом, заключаем: sin α = −0,5.

Задача. Найдите tg α, если tg 2 α = 9 и α ∈ [0; π/2].

Все то же самое, только для тангенса. Извлекаем квадратный корень: tg 2 α = 9 ⇒ tg α = ±3. Но по условию угол α ∈ [0; π/2] — это I координатная четверть. Все тригонометрические функции, в т.ч. тангенс, там положительны, поэтому tg α = 3. Все!

Содержание

Свойства синуса, косинуса, тангенса и котангенса
Знаки тригонометрических функций по четвертям
Свойство периодичности
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов
Знаки тригонометрических функций по четвертям — примеры определения
Общая информация
Виды углов
Смысл функций
Определение знака
Дополнительные сведения
Построение окружности
Свыше 2ПИ
📺 Видео

Видео:Тригонометрические функции и их знакиСкачать

Свойства синуса, косинуса, тангенса и котангенса

В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.

Первое свойство — знак функции в зависимости от того, какой четверти единичной окружности приналдежит угол α . Второе свойство — периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и — α .

Видео:Знаки тригонометрических функций. 9 класс.Скачать

Знаки тригонометрических функций по четвертям

Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?

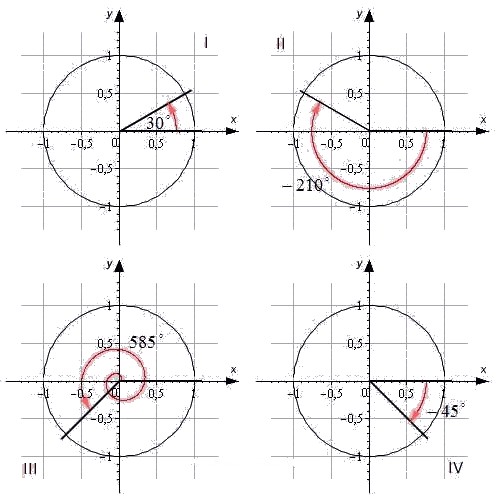
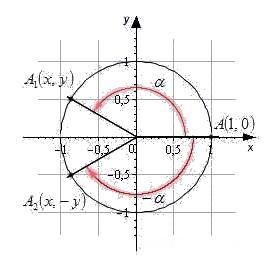
Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A 0 ( 1 , 0 ) и, поворачивая ее вокруг точки O на угол α , попадем в точку A 1 ( x , y ) . В зависимости от того, в какой четверти будет лежать точка A 1 ( x , y ) , угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно.

Для наглядности приведем иллюстрацию.

Угол α = 30 ° лежит в первой четверти. Угол — 210 ° является углом второй четверти. Угол 585 ° — угол третьей четверти. Угол — 45 ° — это угол четвертой четверти.

При этом углы ± 90 ° , ± 180 ° , ± 270 ° , ± 360 ° не принадлежат ни одной четверти, так как лежат на координатных осях.

Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.

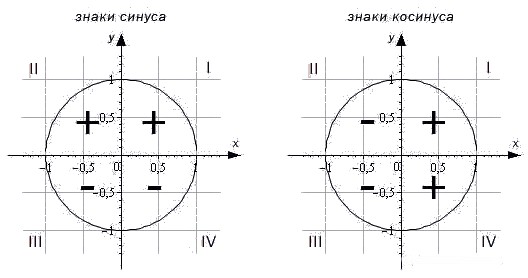
Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус — это ордината точки A 1 ( x , y ) . Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна.

Косинус — это абсцисса точки A 1 ( x , y ) . В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.

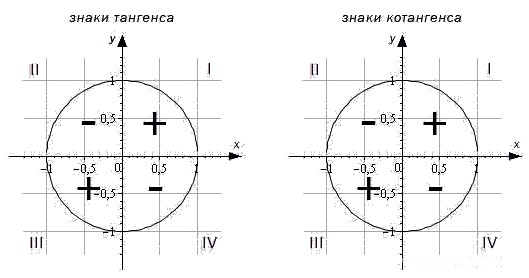
Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным. Аналогично определяются знаки котангенса по четвертям.

Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус — в 3 и 4 четвертях.
Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус — в 2 и 3 четвертях.
Тангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
Котангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.

Видео:Знаки синуса, косинуса, тангенса ЛекцияСкачать

Свойство периодичности

Свойство периодичности — одно из самых очевидных свойств тригонометрических функций.

При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.

Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A 1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса.

Математически данное свойство записывается так:

sin α + 2 π · z = sin α cos α + 2 π · z = cos α t g α + 2 π · z = t g α c t g α + 2 π · z = c t g α

Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.

sin 13 π 5 = sin 3 π 5 + 2 π = sin 3 π 5

t g ( — 689 ° ) = t g ( 31 ° + 360 ° · ( — 2 ) ) = t g 31 ° t g ( — 689 ° ) = t g ( — 329 ° + 360 ° · ( — 1 ) ) = t g ( — 329 ° )

Видео:Найти знак тригонометрической функции (bezbotvy)Скачать

Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов

Вновь обратимся к единичной окружности.

Точка A 1 ( x , y ) — результат поворота начальной точки A 0 ( 1 , 0 ) вокруг центра окружности на угол α . Точка A 2 ( x , — y ) — результат поворота начальной точки на угол — α .

Точки A 1 и A 2 симметричны относительно оси абсцисс. В случае, когда α = 0 ° , ± 180 ° , ± 360 ° точки A 1 и A 2 совпадают. Пусть одна точка имеет координаты ( x , y ) , а вторая — ( x , — y ) . Вспомним определения синуса, косинуса, тангенса, котангенса и запишем:

sin α = y , cos α = x , t g α = y x , c t g α = x y sin — α = — y , cos — α = x , t g — α = — y x , c t g — α = x — y

Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.

Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов

sin — α = — sin α cos — α = cos α t g — α = — t g α c t g — α = — c t g α

Согласно этому свойству, справедливы равенства

sin — 48 ° = — sin 48 ° , c t g π 9 = — c t g — π 9 , cos 18 ° = cos — 18 °

Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Знаки тригонометрических функций по четвертям — примеры определения

Видео:§135 Знаки тригонометрических функций по четвертямСкачать

Общая информация

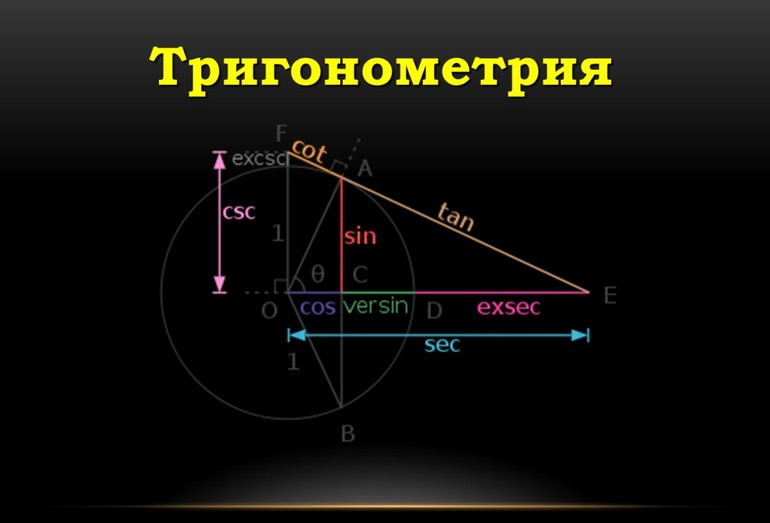
Раздел математики, который занимается изучением тригонометрических функций, называется тригонометрией. К функциям относятся следующие: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg). Существуют также и обратные им функции: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg).

Для нахождения знаков тригонометрических функций по четвертям рекомендуется применять специальный «инструмент». Он называется окружностью синусов и косинусов. Однако по ней можно находить не только функции, которые соответствуют ее названию, но и другие. Делается это с помощью тригонометрических тождеств.

Специалисты рекомендуют для понимания материала получить базовые знания об углах и основных тригонометрических функциях. Следует применять принцип «от простого к сложному», поскольку нужно учитывать физиологические особенности головного мозга.

Виды углов

Важной «ступенью» в освоении тригонометрии является идентификация углов. Они делятся на 7 видов. Кроме того, существует еще два типа классификации по знаку: положительные и отрицательные.

Для составления критериев, по которым математики классифицируют углы, необходимо ввести некоторую переменную. Пусть существует некоторый угол a, градусная мера которого составляет x градусов. Необходимо рассмотреть 7 случаев, в которых он измеряется только в градусной размерности:

Последний случай встречается очень часто в различных задачах, в которых следует вычислить определенное значение, упростить тригонометрическое выражение или использовать формулы приведения, а также найти разность между функциями.

Градус — это не единственная единица измерения размерности угла. Существует также и радиан, который пользуется большей популярностью, чем предыдущая единица. Согласно статистике, которая составлена математиками, при решении задач с тригонометрическим уклоном многие используют радиан (около 95,88%). Это объясняется удобством, поскольку в основном применяется тригонометрическая окружность для быстрого нахождения значений функций. Перевод одной единицы в другую осуществляется с помощью двух простых соотношений:

В радианы: P = (a * ПИ) / 180.
В градусы: а = (P * 180) / ПИ.

Существует 2 метода перевода: автоматизированный и ручной. В первом случае следует применять специальные радианные таблицы, программы и тригонометрическую окружность. Во втором — пользоваться формулами для преобразований. Если очень часто приходится решать задачи подобного типа, то можно создать свой инструмент. Для этого потребуется табличный процессор EXCEL. Необходимо вбить в ячейки две формулы, и тогда ручной метод «превратится» в автоматизированный.

Смысл функций

Тригонометрические функции используются не только в математике, но и в других дисциплинах (физике, электронике, микросхемотехнике, акустике и так далее). С их помощью можно описывать законы изменения различных периодических величин.

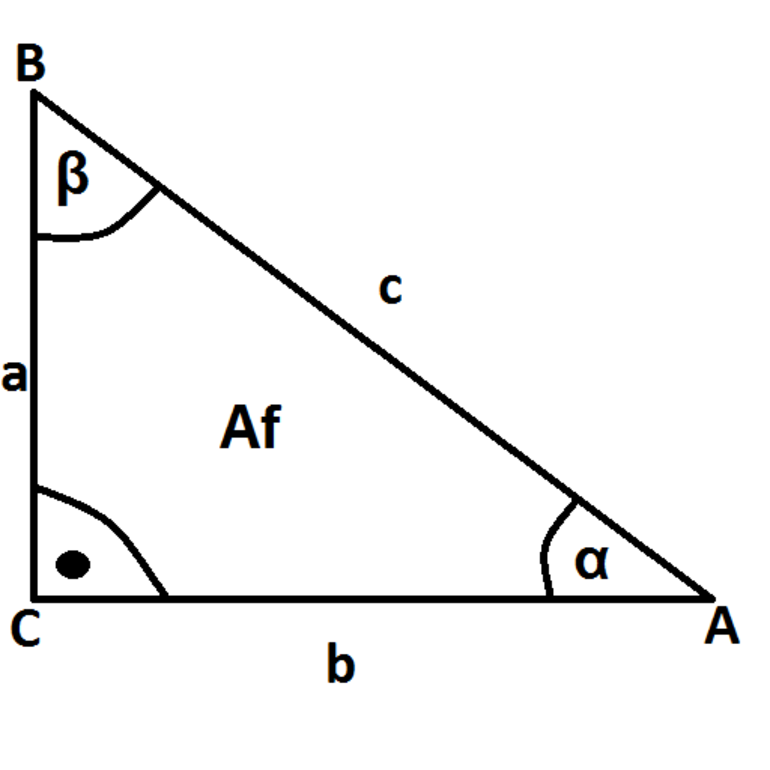
Для определения функции необходимо представить прямоугольный треугольник. Его стороны называются катетами и гипотенузой. Угол между двумя катетами является прямым, то есть он равен 90 градусам.

Синус угла — значение, которое вычисляется отношением линейного размера противолежащего катета к гипотенузе прямоугольного треугольника. Если выразить величину через отношение прилежащего катета к гипотенузе, то она называется косинусом угла. Величина, полученная при отношении двух катетов — противолежащего к прилежащему, называется тангенсом. В случае с котангенсом, необходимо поменять числитель и знаменатель местами, то есть отношение прилежащего к противолежащему. Следует также напомнить, что все четыре функции обладают периодичностью. Для sin и cos период соответствует 2 ПИ, а для tg и ctg — ПИ.

Обратными тригонометрическими функциями являются arcsin, arccos, arctg и arcctg. Их необходимо использовать в том случае, когда нужно найти угол по заданному значению. Для этих целей применяются таблицы Брадиса, тригонометрический калькулятор и программное обеспечение, а также круг синусов и косинусов.

Видео:Знаки тригонометрических функций. Практическая часть. 9 класс.Скачать

Определение знака

Достоверность результата зависит от правильного решения. Неверный знак функции способен кардинально его изменить. Для безошибочного определения значений потребуются еще кое-какие знания. К ним относятся следующие: понятие о системе координат и теорема Пифагора, а также умение чертить окружность с определенным радиусом.

Системы координат, которые применяются при решении задач бывают полярными и декартовыми. Последние используются чаще, чем первые. Полярные применяются для решения задач из области высшей математики, а также в других сложных дисциплинах с физико-математическим уклоном.

Дополнительные сведения

Для определения знака применяется обыкновенная система координат с двумя осями. Одна из них (ОХ) является осью абсцисс, а другая (ОУ) — ординат. Ее центром, который совпадает с центром тригонометрической окружности, является точка «О». Очень часто для работы необходимо знание теоремы Пифагора. Ее формулировка имеет следующий вид: в любом прямоугольном треугольнике выполняется равенство квадрата гипотенузы и суммы квадратов катетов. Вторая формулировка записывается в виде формулы: с^2 = a^2 + b^2 (c, a и b — гипотенуза и два катета соответственно).

Необходимо обратить внимание на следующий факт: сумма всех углов треугольника составляет 180 градусов, то есть является развернутым углом. Математически утверждение можно записать следующим образом через углы а, b и c: а + b + c = 180. Кроме того, существуют и другие соотношения между острыми углами прямоугольного треугольника: cos (a) = sin (b), cos (b) = sin (a), tg (a) = ctg (b), и tg (b) = ctg (a).

Чтобы найти знаки тангенса и котангенса по четвертям, используются такие соотношения: tg (a) = sin (a) / cos (a) и ctg (a) = cos (a) / sin (a).

Построение окружности

Сделать «инструмент», который значительно ускорит процесс решения задач довольно просто. Для этого нужно построить декартовую систему координат и единичную окружность с центром в точке О (точка пересечения осей абсцисс и ординат). Горизонтальная ось обозначается «х», а вертикальная — «у».

Рекомендуется чертить произвольную окружность. Чертеж должен быть простым и понятным. Это называется масштабирование, при котором изображение не соответствует действительному размеру объекта. Его примером является обыкновенная географическая карта. Кроме того, при проектировании очень мелких деталей применяются чертежи, которые в несколько десятков или сотен раз превышают натуральные размеры. Обозначение точки на плоскости выполняется следующим образом:

Координаты заключаются в круглые скобки и разделяются «;».
На первом месте стоит значение, соответствующее оси абсцисс, а на втором — ординат: (x;y).

Окружность пересекает оси в четырех точках: (1;0), (0;1), (-1;0) и (0;-1). Четвертями называются области, которые делят систему координат на четыре равные части. Отсчет выполняется от первой четверти (x>0 и y>0) против часовой стрелки:

Значения по x и y больше 0 соответствуют первой четверти (I).
II: x 0.
III: x 0 и y 0 и ctg>0.
-sin(ПИ + ПИ/4) = -sin(ПИ/4) = -cos(ПИ/4) = -sqrt(2)/2.
tg(ПИ/4) = ctg(ПИ/4) = -sin(ПИ/4) / -cos(ПИ/4) = 1.

После расчетов нужно выполнить проверку знаков. В III четверти больше нуля только тангенс и котангенс. Однако бывают случаи, когда значение градусной меры угла превышает 360.

Свыше 2ПИ

Существует определенный тип задач, в которых величина градусной меры угла свыше 360 градусов. Например, следует вычислить значения тригонометрических функций угла -26ПИ/6. Решается она следующим образом:

Следует выделить целую часть из -26ПИ/6 и привести к удобному виду: 26/6 = 4 + 2/6 = 4 + 1/3. Угол находится в IV четверти (движение по часовой стрелке).
-sin(4ПИ + ПИ/3) = -sin(ПИ/3) = — sqrt(3)/2.
cos(ПИ/3) = 1/2.
-tg(ПИ/3) = — sqrt(3).
-сtg(ПИ/3) = — 1/sqrt(3).

Во втором, четвертом и пятом пунктах функции являются нечетными. Если посмотреть на график, то движение осуществляется по часовой стрелке, поскольку угол является отрицательным числом. Функция косинуса является четной. Ее числовое значение — положительная величина. Последним этапом считается проверка знаков. Угол находится в IV четверти. Значения функций совпадают.

Таким образом, при решении задач по тригонометрии следует применять тригонометрическую окружность, с помощью которой можно безошибочно определять знак функции.