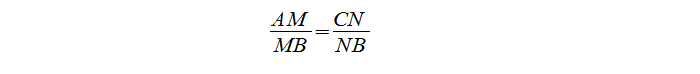Знак пропорциональности треугольников в геометрии

Видео:8 класс, 22 урок, Первый признак подобия треугольниковСкачать

Определение

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Признаки подобия треугольников

I признак подобия треугольников

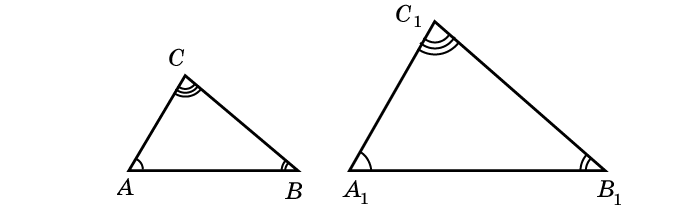
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Свойства подобных треугольников

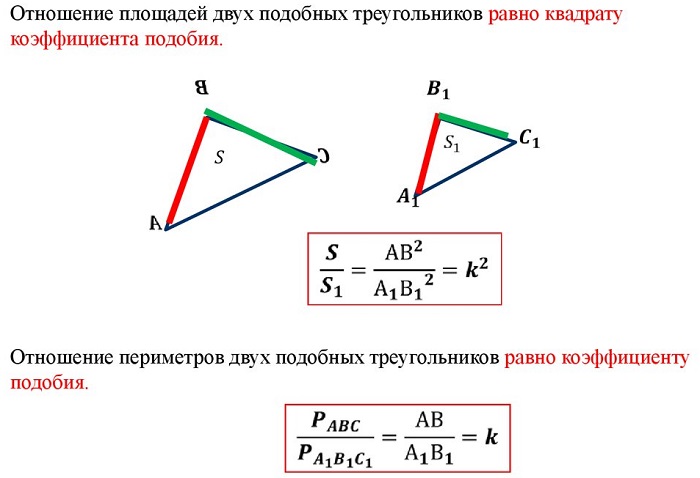
• Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
• Отношение периметров подобных треугольников равно коэффициенту подобия.
• Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Примеры наиболее часто встречающихся подобных треугольников

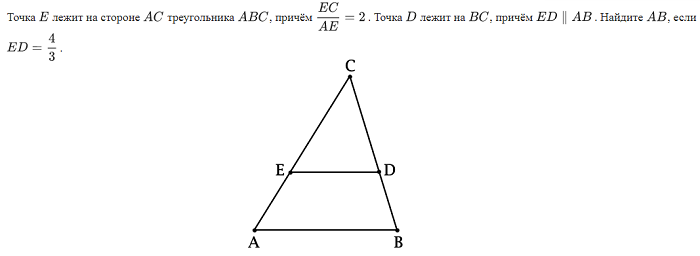
1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Здесь вы найдете подборку задач по теме «Подобные треугольники» .

Видео:Геометрия 8 класс (Урок№15 - Признаки подобия треугольников.)Скачать

Знак подобия в геометрии — правило и примеры обозначения

В учебниках по геометрии часто встречаются задачи на подобие фигур. Какой знак используется для обозначения подобия фигур? Какие фигуры называются подобными? Поговорим обо всем этом в нашей статье.

Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Определение и знак подобия в геометрии

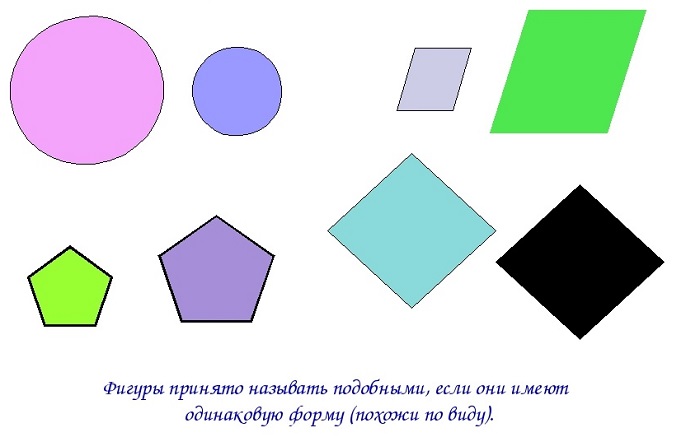
На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.

Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:

Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:

1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.

Видео:8 класс, 20 урок, Определение подобных треугольниковСкачать

Коэффициент подобия треугольников и знак подобия

Часто сверху знака подобия выставляют коэффициент подобия треугольников:

В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.

В алгебре высказываний знаком

обозначают логическую операцию «эквиваленция».

При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):

Видео:8 класс, 19 урок, Пропорциональные отрезкиСкачать

Признаки подобия прямоугольных треугольников

Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.

Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными.

Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.

треугольник ∆ABC и треугольник ∆A₁B₁C₁ считаются подобными при равнозначности углов и пропорциональности сторон;

отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Доказательство подобия треугольников через среднюю линию

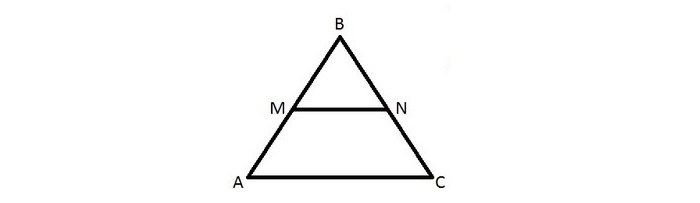
Имеется треугольник ∆ABC, mn — средняя линия. M лежит на AB, N лежит на BC.

Требуется доказательство подобия треугольников ∆MBN и ∆ABC.

Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:

Отсюда делаем вывод, что ∆MBN

∆ABC по II признаку подобия треугольников, что и требовалось доказать.

Видео:7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Примеры решения задач по геометрии на тему «Подобие треугольников»

Видео:ПОДОБНЫЕ ТРЕУГОЛЬНИКИ . §12 геометрия 8 классСкачать

Знак подобия в геометрии — правило и примеры обозначения

В учебниках по геометрии часто встречаются задачи на подобие фигур. Какой знак используется для обозначения подобия фигур? Какие фигуры называются подобными? Поговорим обо всем этом в нашей статье.

Видео:Как использовать подобие треугольников и правильно составить пропорцию. #математика #геометрия #углыСкачать

Определение и знак подобия в геометрии

Подобными называются фигуры, если одна из них представляет уменьшенную копию другой.

На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.

Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:

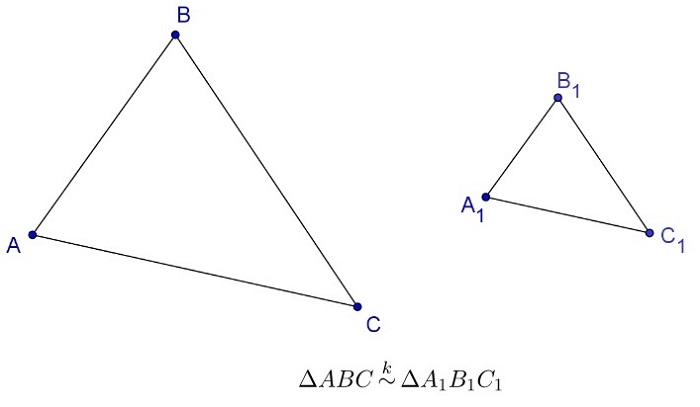
∆A 1 B 1 C 1
— треугольники ABC и A1B1C1
подобны.

Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:

1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.

Видео:Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать

Коэффициент подобия треугольников и знак подобия

Часто сверху знака подобия выставляют коэффициент подобия треугольников:

В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.

В алгебре высказываний знаком

обозначают логическую операцию «эквиваленция».

При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):

Видео:Геометрия 8 класс (Урок№14 - Определение подобных треугольников. Отношение площадей подобных фигур.)Скачать

Признаки подобия прямоугольных треугольников

Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.

Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными.

Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.

треугольник ∆ABC и треугольник ∆A1B1C1 считаются подобными при равнозначности углов и пропорциональности сторон;

отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Видео:Первый признак равенства треугольников. 7 класс.Скачать

Доказательство подобия треугольников через среднюю линию

Имеется треугольник ∆ABC, mn — средняя линия. M лежит на AB, N лежит на BC.

Требуется доказательство подобия треугольников ∆MBN и ∆ABC.

Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:

Отсюда делаем вывод, что ∆MBN

∆ABC по II признаку подобия треугольников, что и требовалось доказать.

Видео:Подобные треугольники. Видеоурок 11. Геометрия 8 классСкачать

Примеры решения задач по геометрии на тему «Подобие треугольников»

📺 Видео

Подобные треугольники - 8 класс геометрияСкачать

8 класс, 24 урок, Третий признак подобия треугольниковСкачать

Подобие прямоугольных треугольников. Среднее геометрическое (пропорциональное). Геометрия 8-9 классСкачать

Задача про соотношение сторон. Геометрия 7 класс.Скачать