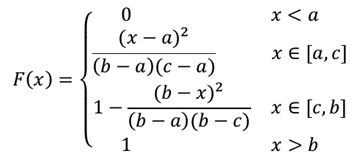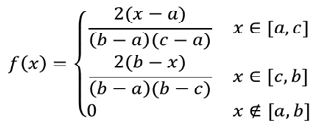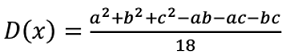Закон распределения для треугольника (2 видео)

Треугольное распределение

Функция треугольного распределения случайной величины определяется формулой:

Плотность треугольного распределения СВ находится по формуле:

Математическое ожидание — формула:

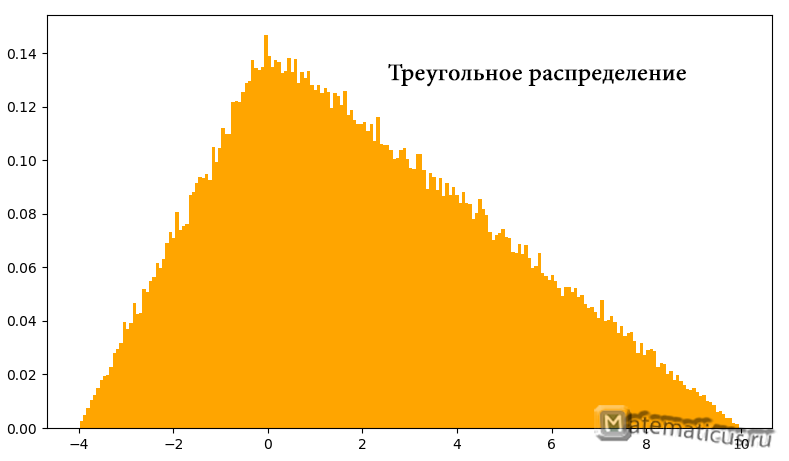
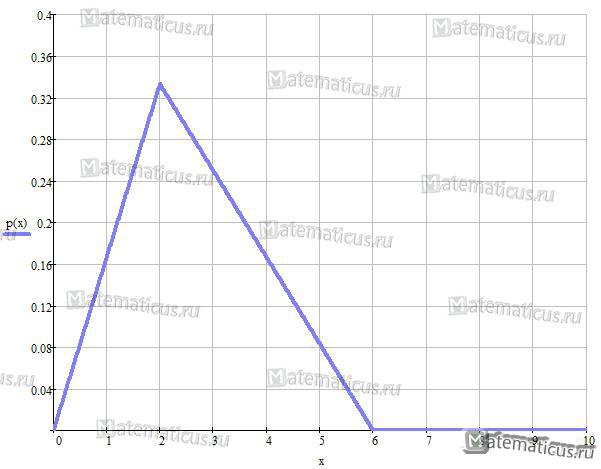
График плотности треугольного распределения случайной величины в диапазоне от -4 до 10

График плотности треугольного распределения случайной величины

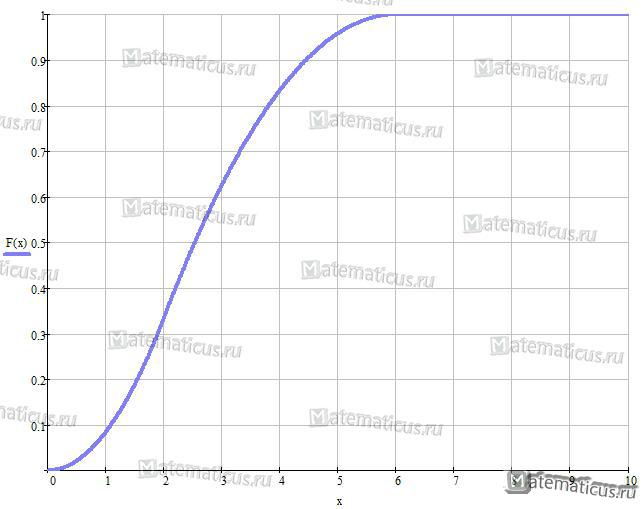
График функции треугольного распределения случайной величины

Треугольное распределения является приблизительной моделью и применяется, когда недостаточно данных или они отсутствуют. Треугольный закон распределения также используется для построения сложных законов распределения.

Содержание

Функция треугольного закона распределения симпсона имеет вид
Равномерное распределение точек в треугольнике
Краткий обзор
1. Квазислучайные последовательности точек
2. Наложение единичного квадрата на треугольник
3. Другие аспекты
Искажение
Другие фигуры
📸 Видео

Видео:Математика без Ху!ни. Ряд распределения дискретной случайной величины. Мат ожидание и дисперсия.Скачать

Функция треугольного закона распределения симпсона имеет вид

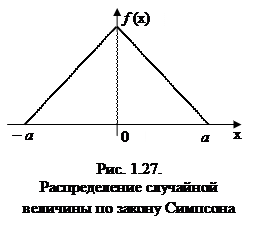К распределению по закону Симпсона приводит сложение двух случайных величин, подчиненных закону равной вероятности при одинаковых параметрах рассеяния. Кривая рассеяния имеет вид равнобедренного треугольника (рис. 1.27), из-за чего закон Симпсона часто называют законом треугольника.

При выборе в качестве начала отсчета случайной величины ее плотность распределения и математическое ожидание имеют следующий вид:

, (1.63)

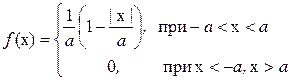
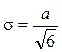
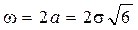
M_x = 0 , , . (1.64)

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: На стипендию можно купить что-нибудь, но не больше. 9137 — | 7300 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Функция треугольного распределения случайной величины определяется формулой:

Плотность треугольного распределения СВ находится по формуле:

Математическое ожидание — формула:

График плотности треугольного распределения случайной величины в диапазоне от -4 до 10

График плотности треугольного распределения случайной величины

График функции треугольного распределения случайной величины

Он характерен для случайных погрешностей цифровых приборов, в которых измеряемая величина преобразуется в пропорциональный интервал времени Т_сч, называемый временем счета, а измерение этого интервала выполняется с помощью счетных импульсов стабильного генератора, имеющих период следования Т . В связи со случайным положением счетных импульсов относительно интервала Т_сч, а также случайным соотношением между периодом Т и временем счета Т_сч треугольный закон представляет собой композицию (объединение) двух равномерных законов с одинаковыми по величине максимальными погрешностями.

Функция распределения одномерной плотности вероятности случайных погрешностей для треугольного закона задается следующими соотношениями:

(46)где

График треугольного закона распределения приведен на рисунке 20.

Математическое ожидание величины x: определяется по той же формуле, что и равномерное:

Рисунок 20 — Треугольное распределение случайной величины

Среднее квадратическое отклонение определяется по формуле:

Видео:Нормальное Распределение за 6 МинутСкачать

Равномерное распределение точек в треугольнике

Большинство двухмерных квазислучайных методов рассчитано на сэмплирование в единичном квадрате. Однако в компьютерной графике также очень важны треугольники. Поэтому я описал простой метод прямого построения для равномерного покрытия последовательностью точек треугольника произвольной формы.

Рисунок 1. Новый прямой метод построения открытой (бесконечной) квазислучайной последовательности с низким расхождением в треугольнике произвольной формы и размера. На рисунке показаны распределения точек в пятнадцати случайных треугольниках для первых 150 точек.

Видео:Функция распределения дискретной случайной величиныСкачать

Краткий обзор

Последовательности с низким расхождением (low discrepancy), равномерно сэмплирующие/заполняющие квадрат, активно изучались почти сотню лет. БОльшую часть этих квазислучайных последовательностей можно расширить до прямоугольников простым растягиванием, не сильно повредив при этом расхождению.

Однако в этом посте мы рассмотрим интересное и важное расширение последовательностей с низким расхождением на произвольный треугольник.

Насколько я мог понять, построению множеств равномерно распределённых в треугольнике точек и последовательностей уделялось очень мало внимания. Примечательные работы недавних лет Басу [2014], Пилландса [2005] и Брандолини [2013] представляют основные, если не единственные статьи по этой теме.

Эти авторы обычно рассматривают эту проблему под очень теоретическим и аналитическим углом, и почти всегда решают её для единичного правильного треугольника. В отличие от них, мой пост в основном предназначен для разработки практических техник в рендеринге графики.

В посте описывается простой метод прямого построения, не требующий ни принятия/исключения, ни отбрасывания или рекурсии; и самое важное то, что его можно применять к треугольникам произвольного размера и формы.

Пост состоит из четырёх разделов:

Квазислучайные последовательности в квадрате
Наложение единичного квадрата на треугольник.
Снижение искажений
Дальнейшие обобщения

Видео:Функция распределения и плотность распределенияСкачать

1. Квазислучайные последовательности точек

Вы можете подумать, что разместить 100 точек в квадрате таким образом, чтобы минимальное расстояние между соседними точками оставалось как можно бОльшим, будет легко. Но что если нужно разместить 13 точек? 47? А как насчёт 2019 точек?!

Оказывается, что последовательности точек с низким расхождением обеспечивают систематический способ решения этой задачи. Существует множество квазислучайных последовательностей с низким расхождением, от простой последовательности Холтона до более сложной последовательности Соболя. Каждая из этих последовательностей имеет свои достоинства и недостатки. Например, последовательности Холтона оказываются более полезными при размещении объектов в области, потому что у неё хорошо оптимизированы такие метрики локального расстояния, как ближайшие соседи. Последовательность Соболя склонна к образованию большей «скученности», однако глобальное распределение точек очень равномерно, поэтому она имеет превосходные свойства квадратуры.

Есть ещё одна последовательность, которую я люблю использовать, с отличными локальными, а также глобальными свойствами. Это последовательность , подробно описанная в моём предыдущем посте «Неожиданная эффективность квазислучайных последовательностей».

Если вкратце, то мы задаём бесконечную двумерную последовательность , такую, что

Подробнее об этом особом значении , которое часто называют «пластической константой» можно прочитать в Википедии или Mathworld.

В итоге, на рисунке 2 показано сравнение различных последовательностей с низким расхождением (и простая равномерная случайная выборка для сравнения). Как видите, эта случайная выборка демонстрирует скапливание точек. При этом в ней есть области, вообще не содержащие точек («белый шум»), в то время как квазислучайная последовательность с низким расхождением — это метод построения (бесконечной) последовательности точек детерминированным образом так, чтобы на любом этапе размещённые точки равномерно распределялись по всему пространству.

Рисунок 2. Иллюстрация первых 150 членов различных квазислучайных последовательностей с низким расхождением. Заметьте, что все они создают более равномерно распределённые в пространстве точки, чем простое равномерное случайное распределение (внизу слева).

Видео:Преобразование звезды сопротивлений в эквивалентный треугольник. Преобразование мостовой схемыСкачать

2. Наложение единичного квадрата на треугольник

Существует три хорошо известных способа, позволяющих обеспечить равномерную случайную выборку из треугольника:

Рисунок 3. Метод параллелограмма

Метод параллелограмма заключается в следующем.

Для треугольника рассмотрим параллелограмм .

Для точки единичного квадрата зададим такую точку , что .

Эта точка всегда будет находиться внутри параллелограмма. Однако если она оказывается в дополнительном треугольнике , то нам нужно отразить её обратно в треугольник .

То есть если , то , но если 1$» data-tex=»inline»/>, то .

Однако очень важно понимать, что даже хотя эти методы обеспечивают равномерную выборку из треугольника, это не означает, что такое преобразование сохранит равномерное пространственное расположение (т.е. низкое расхождение) наших квазислучайных распределений точек.

Например, в случае метода параллелограмма отражение может часто приводить к тому, что точка окажется очень близко к другой существующей точке. Очевидно, что это разрушает структуру с низким расхождением и проявится как искажения/полосы.

Аналогично, метод инверсного распределения накопленных вероятностей применяет к точкам нелинейное искажение. В последовательностях Холтона и Соболя это означает, что две точки очень часто подталкиваются очень близко друг к другу.

На рисунке 4 показано, насколько хорошо сохраняется низкое расхождение в каждой из различных квазислучайных последовательностей при преобразовании области из единичного квадрата в треугольник при использовании метода параллелограмма.

Рисунок 4. Сравнение преобразования различных квазислучайных последовательностей в треугольнике. Вверху показана последовательность Холтона, посередине — последовательность Соболя, внизу — последовательность . Видно, что в последовательности Холтона возникает значительная скученность точек, а в последовательности Соболя — значительное образование полос. По сравнению с ними, в последовательности точки распределены очень равномерно, и почти отсутствует заметная скученность или полосы.

Из трёх различных методов триангуляции и множества различных квазислучайных последовательностей метод параллелограмма, применённый к методу последовательности , является единственной комбинацией, постоянно создающей результаты, приемлемые с точки зрения сохранения низкого расхождения без искажений.

Превосходные результаты этого сочетания можно подробнее рассмотреть на рисунке 5.

Рисунок 5. Можно увидеть, что преобразованная последовательность обеспечивает очень простой, но эффективный способ равномерного распределения множества из точек в треугольнике. Он работает и с остроугольными, и с тупоугольными треугольниками. (Цвет обозначает порядок расположения).

Видео:Что такое Треугольник Карпмана?Скачать

3. Другие аспекты

Видео:Распределение Пуассона – закон редких событий // Vital MathСкачать

Искажение

Метод параллелограмма требует выбора двух сторон треугольника в качестве базисных векторов.

Если вершины помечаются в случайном порядке, то паттерны точек обычно напоминают показанные на рисунке 6.

Рисунок 6. Паттерны точек, получающиеся при случайном выборе порядка вершин. Заметьте, что в большинстве случаев явно заметно искажение.

Однако оказывается, что при продуманном выборе порядка вершин можно значительно снизить искажения. Наиболее примечательно то, что если треугольник пометить так, что является наибольшим углом (то есть против него лежит наибольшая сторона), то стороны и используются в качестве двух сторон параллелограмма.

Если принять такой порядок, то получаются паттерны точек, показанные выше на рисунках 1, 4 и 5.

Однако даже при определённом порядке вершин в некоторых случаях всё равно заметны эффекты искажений. Больше всего они заметны, когда в треугольниках один из углов очень мал. В случае тупоугольных треугольников, когда наименьший угол меньше 30 градусов, то заметно некоторое искажение, а в случае остроугольных треугольников, когда наименьший угол меньше 20 градусов, становится видным искажение. (Если сэмплируемые треугольники являются частью сетки Делоне, то такие проблемы с искажениями могут быть минимальными, потому что триангуляция Делоне специально предназначена для минимизации количества треугольников с малыми углами.)

Видео:Теория вероятностей #12: случайная величина, плотность и функция распределенияСкачать

Другие фигуры

К сожалению, технику параллелограмма невозможно использовать для других фигур, потому что в нём используется симметрия треугольника. Для некоторых фигур можно получить хорошие результаты с помощью метода инверсного распределения накопленных вероятностей. Ниже показан пример того, как последовательность с низким расхождением можно преобразовать в область, ограниченную гауссовой кривой с сохранением равномерного расстояния между точками.