Задано множество точек и множество окружностей

Представим на координатной плоскости множество точек, удовлетворяющих условию х = 5 и х = -4,

В первом случае прямые параллельны оси ординат, во втором – абсцисс.

На прямой может быть расположено неограниченное количество точек. И у всего этого множества точек, координаты удовлетворяют условиям х = 5 и х = -4; у = -4 и у = 1.

На координатной прямой неравенству х 3. Проанализируем, что это за точки:

— множество точек, абсцисса которых больше или равна 3

— точки, лежащие правее прямой х = 3 и на прямой.

Алгоритм построения будет иметь вид:

— строим в координатной плоскости прямую: х = 3;

— определяем, где будут находиться точки, абсцисса которых больше 3; ответ – правее;

— множество всех точек удовлетворяющих условию х > 3 покажем при помощи штриховки;

х > 3 задает полуплоскость, находящаяся правее прямой х = 3 и все точки этой прямой. Прямую изображаем одной цельной линией, этим указываем, что все точки расположенные на прямой так же включены во множество.

Представим множество точек, удовлетворяющих условию у 1.

Постройте множество точек у > 1. По аналогии, точкам этого множества присуще свойство — у них ордината больше 1.

Следовательно, они будут находиться выше прямой у = 1. В соответствии со знаком неравенства точки прямой у = 1 не удовлетворяют условию y > 1. Графически мы это покажем, изобразив прямую у = 1 пунктиром.

Представим множество точек, соответствующих условию у > 1 так:

Представим на координатной плоскости множества точек, соответствующих условию: -2 ≤ х ≤ 2.

А — множество точек окружности, В — множество точек прямой Л?

Математика | 10 — 11 классы

А — множество точек окружности, В — множество точек прямой Л.

Из скольких элементов может состоять пересечение данных множест?

Может ли оно быть пустым?

Количество элементов пересечения множеств = количество точек пересечения окружности и пряммой, что дает варианты

1) два элемента — прямая пересекает окружность в двух точках (секущая)

2) один элемент — прямая касается окружности (в одной точке) (касательная)

3) пустое множество — прямая и окружность не имеют общих точек.

Данную прямую пересекают четыре прямые?

Данную прямую пересекают четыре прямые.

Сколько может образоваться точек пересечения этих прямых с данной?

Запишите с помощью обозначений соотношение между данными множествами : 1) А — множество квадратов, а В — множество прямоугольников ; 2) С — множество точек, окружности с центром в точке О?

Запишите с помощью обозначений соотношение между данными множествами : 1) А — множество квадратов, а В — множество прямоугольников ; 2) С — множество точек, окружности с центром в точке О.

D — множество точек принадлежащихкругу с центром в той же точке О.

Соотношение между множествами изобразите кругами Эйлера — Венна.

Задать неравенством множество точек?

Задать неравенством множество точек.

А)Даны окружность и на ней точки А и В?

А)Даны окружность и на ней точки А и В.

Найдите множество точек пересечения медиан всех треугольников АВС с вершиной С на этой окружности.

Б) найдите множество точек пересечения биссектрис всех треугольников АВС с вершиной С, лежащей на этой окружности.

Пусть А множество натуральных чисел , кратных 4, B множество натуральных чисел , кратных 6 ?

Пусть А множество натуральных чисел , кратных 4, B множество натуральных чисел , кратных 6 .

Назовите несколько элементов множества А пересечения с B .

Укажите наименьший элемент этого множества .

Как его называют ?

Прямые, имеющие множество бесконечных точек называют?

Прямые, имеющие множество бесконечных точек называют?

Множество K содержит 7 элементов, множество L 9 элементов?

Множество K содержит 7 элементов, множество L 9 элементов.

Если пересечение этих множеств содержит 4 элемента, то сколько элементов содержит их объединение?

Среди данных множеств укажите пустые множества : а) множество людей на Луне ; б) множество точек пересечения у 2 — х различных параллельных прямых?

Среди данных множеств укажите пустые множества : а) множество людей на Луне ; б) множество точек пересечения у 2 — х различных параллельных прямых.

Множество точек на отрезке?

Множество точек на отрезке?

Множество точек на прямой?

Множество делителей числа 12?

Множество кратных числа 12?

Множество K содержит 7 элементов, множество L 9 элементов?

Множество K содержит 7 элементов, множество L 9 элементов.

Если пересечение этих множеств содержит 4 элемента, то сколько элементов содержит их объединение?

На этой странице находится вопрос А — множество точек окружности, В — множество точек прямой Л?, относящийся к категории Математика. По уровню сложности данный вопрос соответствует знаниям учащихся 10 — 11 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Математика. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

(X — 5)(x + 5) / x(x — 6) * (x — 6)(x + 6) / x(x + 5) = (x — 5)(x + 6) / x ^ 2.

1)17 — 8 = 9(кг) 2)9 + 6 = 15(кг) Ответ : 15 кг ваниль.

Извини, могу только Второй : — — — — — — — — — — — — — — — — — — — — — — — — — 1 / x + 1 / y = 3 / 8 x + y = 12 — — — — — — — — — — — — — — — — — — — — — — — — — — 1 / (12 — y) + 1 / y — 3 / 8 = 0 * 8y(12 — y) x = 12 — y — — — — — — — — — — — — — -..

Четыре : юнош, ноша, юн, наш.

Сами думайти а чё тупые ну ладно будет хрен.

А) 1. 900 : 100 = 9 — 1% 2. 9 * 15 = 135 рублей стоит зонт б) 1. 240 / 100 = 2, 4 — 1% 2. 2, 4 * 30 = 72 км / ч.

№1. х — второе число (х + 24) — первое число (х — 10) — третье число Сумма всех чисел равна 116 х + (х + 24) + (х — 10) = 116 3х + 14 = 116 3х = 116 — 14 3х = 102 х = 34 (второе число) 34 + 24 = 58 ( первое число) 34 — 10 = 24 ( третье число) Ответ .

Х — 1 число х — 24 — 2 число х — 34 — 3 число х + х — 24 + х — 34 = 116 3х = 116 + 58 3х = 174 х = 174 : 3 х = 58 — 1 число 58 — 24 = 34 — 2 число 34 — 10 = 24 — 3 число — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — 58 + 34 + 24 = 116 х..

Не видно не видно не видноне видно не видно.

2. 7 + 2 * 9y = 4. 3 2 * 9y = 4. 3 — 2. 7 2 * 9y = 1. 6 y = 1. 6 : 2 * 9 y = 7. 2.

Лекция 5. Метод геометрических множеств

Геометрическим множеством (ГМ) называется множество геометрических элементов (ГЭ), обладающих каким-либо общим геометрическим свойством.

5.1. Геометрические множества

Геометрические множества некоторых геометрических элементов

ГМ точек	ГМ прямых	ГМ плоскостей
1. Удаленных от заданной точки О на расстояние l
Сфера радиусом l с центром в точке О.	Совокупность прямых, касательных к сфере радиусом l с центром в точке О.	Совокупность плоскостей, касательных к сфере радиусом l с центром в точке О.
2. Удаленных от данной прямой m на расстояние l
Цилиндрическая поверхность радиусом l и осью m.	Совокупность прямых, касательных к поверхности цилиндра радиусом l и осью m, а также все образующие этой цилиндрической поверхности.	Совокупность плоскостей, касательных к поверхности цилиндра радиусом l и осью m.
3. Удаленных от данной плоскости σ на расстояние l
Две плоскости τ 1 и τ 2 //σ, расположенные по разные стороны от неё на расстоянии l
4. Равноудаленных от точек А и В
Все точки плоскости σ⊥АВ, проходящей через середину отрезка АВ.	Совокупность прямых, касательных к поверхностям сфер равного диаметра с центрами в точке А и В.	Совокупность плоскостей, касательных к поверхностям сфер равного диаметра с центрами в точке А и В.
5. Равноудаленных от двух параллельных прямых
Плоскость, проходящая через середину отрезка (расстояния между данными прямыми) и перпендикулярная ему.	Совокупность прямых, лежащих в плоскости, проходящей через сере-дину отрезка (расстояния между данными прямыми) и перпендикулярной ему.	Плоскость, проходящая через середину отрезка (расстояния между данными прямыми) и перпендикулярная ему, а также две плоскости, касательные к двум цилиндрическим поверхностям с осями – данными прямыми и равного диаметра.

5.2. Алгоритм решения задач методом геометрических множеств

1. 1. Условие задачи разбиваем на ряд простейших условий, каждому из которых должно отвечать определенное свойство искомого элемента (или элементов).

1. 1. Для каждого простейшего условия определяем удовлетворяющее ему геометрическое множество элементов.

1. 1. Находим общее решение задачи как некое геометрическое множество элементов, удовлетворяющих одновременно всем простейшим условиям. Оно представляет собой пересечение выбранных элементарных геометрических множеств.

1. Проводим анализ возможных решений, цель которого выявить когда, сколько и каких решений может быть в данной задаче в зависимости от взаимного положения заданных геометрических элементов, а, следовательно, связанных с ним геометрических множеств.

Упражнение

1. На заданной прямой m построить точку, удаленную от точки О на расстояние l (Рисунок 5.1).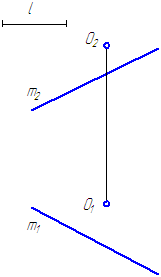

Рисунок 5.1
I. Геометрическое решение в пространстве

1. Искомые точки должны принадлежать прямой m, следовательно, решение по первому условию – любая точка на прямой.
2. Множество точек, удаленных от точки О на расстояние l образуют в пространстве сферу, с центром в точке О и радиусом равным l.
3. Общее решение задачи – точки, одновременно принадлежащие прямой m и сфере, то есть точки пересечения прямой m со сферой.

II. Графическое решение задачи (Рисунок 5.2).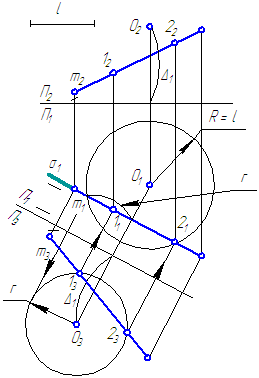

Рисунок 5.2
III. Анализ возможных решений (Рисунок 5.3).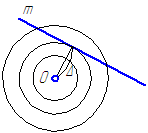

Рисунок 5.3

Обозначим Δ – расстояние от точки О до прямой m:

• l > Δ – прямая пересечет сферу в двух точках;
• l = Δ – m – касательная к сфере → одна точка;
• l Краткая запись построения

1. 1. Строим проекцию сферы с центром в точке О и радиусом l.

1. 1. Через прямую m проводим секущую плоскость, например, σ⊥π₁. Плоскость σ пересекает сферу, в сечении – окружность.
   2. Вводим ДПП π₃⊥π₁ и π₃//σ.

1. Строим на π₃ проекции прямой m и окружности сечения, определяем точки пересечения прямой с окружностью, которые являются искомыми.

Упражнение

2. В плоскости σ=ΔАВС через точку А провести прямую AD, удаленную от точки О на расстояние l (О∈σ) (Рисунок 5.4). Геометрическое решение в пространстве

1. Прямая AD, удаленная от точки О на расстояние l, является касательной к сфере радиусом R_сф = l с центром в точке О.
2. Прямая AD∈σ.

Плоскость σ пересекает сферу по окружности.
Искомая прямая AD – касательная к окружности сечения плоскости σ и сферы.
II. Графическое решение задачи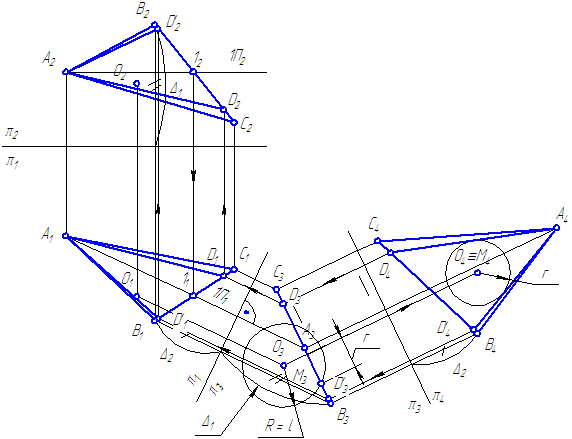

Рисунок 5.4
III. Анализ возможных решений
Обозначим Δ – расстояние от точки О до плоскости σ:

• l > Δ – плоскость пересечет сферу по окружности, → две прямые, проходящие через точку А и касательные к окружности сечения (если точка А вне окружности); если точка А на окружности сечения – одна прямая;если точка А внутри окружности сечения – решения нет;
• l = Δ – плоскость касается сферы → одна прямая, проходящая через точку А и точку касания; если точка А совпала с точкой касания → бесконечное множество прямых принадлежащих плоскости σ;
• l Краткая запись построения
  Находим истинную величину треугольника АВС, например, с помощью введения ДПП:

1. π₃⊥π₁ и π₃⊥σ.
2. π₄⊥π₃ и π₄//σ.
3. Строим окружность сечения σ со сферой. Строим касательные к этой окружности, проходящие через точку А.

5.3. Задачи для самостоятельной работы

1. Задана плоскость α=∆АВС и прямая m – общего положения. Определить угол между прямой m и плоскостью α. 2. Задана плоскость α=∆АВС и точка D вне плоскости. Повернуть точку D так, чтобы она совпала с плоскостью α. Ось вращения i⊥π₁.

🌟 Видео