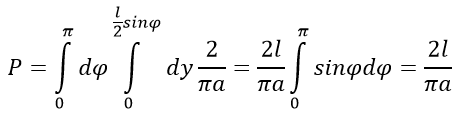Задачу бюффона при заданных длине иглы и расстоянии между параллельными прямыми

Метод Бюффона основан на методе Монте-Карло и заключается в бросании иглы на плоскость, расчерченную на расстоянии друг от друга параллельными прямыми. Этот метод также применяется для вычисления числа π. Чем больше количества повторений опыта, тем точнее будет результат.

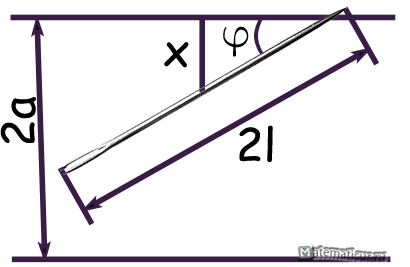
Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 2а. На плоскость наудачу бросают иглу длины 2l (2l≤2а), φ – угол. Найти вероятность того, что игла пересечет какую-нибудь прямую.

Решение

Графически задачу Бюффона можно представить следующем образом: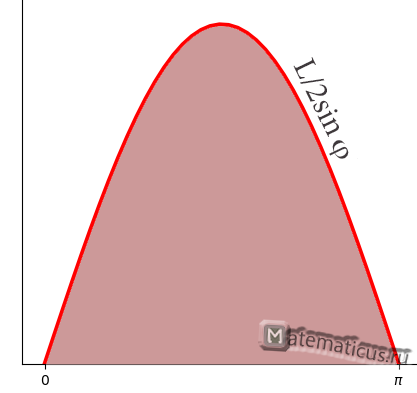

Найдем вероятность через вычисления интеграла:

Экспериментально по методу Монте-Карло вероятность определяется по формуле:

P≈[кол-во бросаний]/[кол-во пересечений]

Число π приближенно можно определить по методу Монте-Карло по формуле:

π≈2L*[кол-во бросаний]/ a *[кол-во пересечений]

a — расстояние между линиями.

Если мы сделаем предположение, что длина иглы равна расстоянию между линиями, то выражение определяется по формуле:

π≈ 2 *[кол-во бросаний] / [кол-во пересечений]

В практических вычислений вероятности также используют условие, что параллельные линии находятся друг от друга на расстояние двух длин иглы

Видео:Теория вероятностей 11: задача о бросании иглыСкачать

Элегантное доказательство задачи Бюффона о бросании иглы

Несколько лет тому назад я готовился к научно-популярной презентации, в которой рассказывал о числе Пи. Одна из тем была задача Бюффона о бросании иглы. Это любопытный эксперимент о том, как связано бросание иглы на лист бумаги и число Пи.

Тогда в подготовке мне сильно помогла эта статья. В отпускe я начал читать Владимира Игоревича Арнольда книжку «Математическое понимание природы» и наткнулся в ней на элегантное доказательство-рассуждение.

Далее, мой пересказ с иллюстрациями.

Задача

Возьмем лист бумаги, разлинованный параллельными прямыми такими, что расстояние между соседними равно $inline$1$inline$. Бросим случайно иглу длины $inline$1$inline$ на этот лист бумаги. Повторим этот опыт много раз. Пусть $inline$N$inline$ — число всех попыток, а $inline$M$inline$ число пересечений упавшей иглы с линиями на бумаги. Как будет расти с $inline$N$inline$ число пересечений $inline$M$inline$?

Решение

Отношение числа пересечений к числу всех попыток будет стремиться к константе

Таким образом, если бросить иглу достаточное число раз, то можно получить хорошее приближение к числу Пи.

Доказательство

1. При $inline$Nrightarrowinfty$inline$ число пересечений будет асимптотически равно $inline$M sim cN$inline$. Здесь $inline$c$inline$ постоянная, означающая вероятность падения иглы на линию при одном бросании.
2. Возьмем иглу длиной $inline$2$inline$, тогда число пересечений тоже увеличится в два раза. Удлиняющая половина иглы тоже игла длины $inline$1$inline$, и она тоже падает случайно.
3. Иглу можно изогнуть. Обе половины дадут прежнее пересечение, а вместе в два раза больше.

Давайте теперь будем бросать кривую иглу длиной $inline$l$inline$, тогда при $inline$Nrightarrowinfty$inline$ число пересечений будет $inline$M sim cNl$inline$

И напоследок будем бросать окружность диаметром $inline$d=1$inline$.
Длина такой окружности $inline$l=pi d= pi$inline$. При $inline$Nrightarrowinfty$inline$ число пересечений будет асимптотически равно $inline$M sim cNpi$inline$.

Видео:Эксперимент с числом пи: находим 3.14 при помощи иголки. Задача БюффонаСкачать

Иголка и вероятность

Видео:Задача Бюффона об иглеСкачать

Задача

Плоскость расчерчена параллельными прямыми. Расстояние между любыми двумя соседними прямыми равно 1. На плоскость падает иголка фиксированной длины l (l ≤ 1).

Найдите вероятность, с которой иголка пересечёт хотя бы одну из прямых (то есть имеет общие точки хотя бы с одной из прямых).
Считаем, что иголка не имеет толщины (представляет собой просто отрезок) и что она падает и лежит на плоскости плашмя, а не втыкается в неё.

Видео:Игла Бюффона, или новая задача на вероятность в ЕГЭСкачать

Подсказка 1

Что понимается под вероятностью некоторого события?

1. Сначала договоримся, что мы будем понимать под событием. Пусть мы проводим серию одинаковых опытов — испытаний, в каждом из которых одни и те же начальные условия и результат очередного испытания никак не зависит результатов предыдущих. Хрестоматийные примеры: подбрасывание «идеальной» монетки, бросание «идеального» игрального кубика. Или, как у нас в задаче, — бросание иголки на разлинованную плоскость.

У каждого испытания есть разные элементарные исходы. Например, выпадение числа от 1 до 6 в примере с кубиком. Событием называется какое-то подмножество множества элементарных исходов. Например, «выпадение 2». Или «выпадение нечётного числа» (то есть выпадение 1, 3 или 5). Можно рассматривать более сложные испытания, вроде подбрасывания пяти монеток. Здесь элементарными исходами будут такие: «выпало пять орлов», «выпало четыре орла и одна решка», и так далее. В качестве события можно рассмотреть, например, такое: «выпало не меньше трёх орлов».

В нашей задаче испытание — это одно бросание иголки, а нужное нам событие — это пересечение хотя бы одной линии.

2. Под вероятностью события можно понимать отношение числа благоприятных для этого события исходов к числу всех возможных исходов (отсюда получается, что вероятность — это всегда число от 0 до 1). Например, вероятность события «выпадение нечётного числа» при бросании одного кубика равна 1/2, потому что подходит ровно половина от всех возможных исходов. Вероятность события «выпало не меньше трёх орлов» при бросании 5 монеток также равна 1/2.

Такое определение вероятности отлично работает, когда множество возможных исходов конечно. Но в нашей задаче бесконечно много исходов — положений упавшей иголки. Да и подходящих исходов тоже бесконечно много. Как же быть? Немного подкорректируем наше «определение»: вероятность события — это доля, которую благоприятные исходы «занимают» во множестве всех исходов. С таким «определением» уже можно посчитать требуемую в задаче вероятность.

Честно говоря, всё сказанное выше является «объяснением на пальцах», и это нельзя рассматривать со всей математической строгостью. Но для наших целей такого подхода вполне достаточно.

3. Для ясности еще один пример. Рассмотрим квадрат, и соединим в нём середины двух соседних сторон отрезком, отсекая таким образом уголок. После этого будем случайным образом тыкать иголкой в квадрат. С какой вероятностью мы попадём внутрь уголка? Здесь исход каждого испытания — то, куда попал конец иголки, то есть одна точка внутри квадрата. Ясно, что исходов бесконечно много и что подходящих нашему событию исходов — попаданию в уголок — тоже бесконечно много. Поэтому про количества исходов для вычисления вероятности рассуждать уже бессмысленно. На зато долю вычислить можно — это просто отношение площадей уголка и квадрата. Оно равно 1/8. Заметим, что границы фигур имеют нулевую площадь, поэтому про них можно не думать. В частности, в отрезок, который отсекал уголок, иголка попадёт с вероятностью 0.

Видео:Игла Бюффона (без интеграла)Скачать

Подсказка 2

Последний пример из первой подсказки может дать намёк на возможный путь решения задачи. Нужно ввести параметры, которые бы определяли положение иголки и позволяли бы описать все случаи, когда она пересекает линии. Двух параметров здесь вполне достаточно. После этого нужно понять, какие вообще значения могут принимать эти параметры и какие значения описывают наше событие. Если выбрать параметры удачно, то эти условия будут довольно простыми и их можно будет даже «изобразить»: взять координатную плоскость, у которой оси соответствуют параметрам, и нарисовать область, точки которой удовлетворяют полученным условиям. После этого останется лишь посчитать площадь всей области и площадь той её части, которая соответствует пересечению иголки и линий. А затем найти отношение этих площадей.

Видео:Теоремы об углах, образованных двумя парал. прямыми и секущей | Геометрия 7-9 класс #30 | ИнфоурокСкачать

Решение

Условимся, что прямые из условия идут горизонтально. Вот мы бросили иголку на плоскость. Как описать её расположение, чтобы было удобно учитывать пересечение с прямыми? Заметим своеобразную симметрию: нам не так уж и важно, на какую именно (или какие, если их две) полосу между прямыми упадёт иголка — полоски все одинаковые. Также ясно, что сдвиги по горизонтали тоже ни на что не влияют. А вот что действительно важно — это как «далеко» иголка лежит от прямых и под каким углом она к ним наклонена. Поэтому в качестве параметров из второй подсказки можно взять угол наклона α иголки к прямым и расстояние d от середины иголки до ближайшей прямой (рис. 1). Таким образом мы используем ещё одну возникшую в задаче «симметрию».

Какие значения могут принимать эти параметры? Радианная мера угла α меняется от 0 до π, а d принимает значения от 0 (если середина иголки попала на прямую) до 1/2 (дальше середина иголки от прямых быть не может). На плоскости с координатами (α, d) эти ограничения задают прямоугольник (рис. 2).

Из рисунка 3 видно, при каком условии на α и d иголка пересекает хотя бы одну прямую: проекция половины иголки на направление, перпендикулярное прямым, должна быть больше d. То есть должно выполняться неравенство .

Вот мы и получили описание всех случаев, когда иголка пересекает хотя бы одну прямую (пересечение с двумя прямыми будет, только если одновременно выполнены равенства α = π/2 и d = 1/2, что может дать всего одну точку в нашем прямоугольнике — бесконечном множестве всех возможных значений пары параметров). Осталось вычислить площадь под графиком синусоиды и разделить её на площадь всего прямоугольника, которая равна π/2 (рис. 4).

В итоге получаем, что искомая вероятность равна .

Видео:Длина отрезкаСкачать

Послесловие

Считается, что эту задачу впервые поставил и довольно обстоятельно исследовал французский учёный XVIII века граф де Бюффон — довольно неординарный человек с очень широким кругом интересов, сделавший немало полезного в разных областях знаний. Поэтому часто её называют задачей об игле Бюффона. По-видимому, это была первая задача на так называемую геометрическую вероятность. Как мы видели, суть такого подхода заключается в том, чтобы представить множество элементарных исходов какого-нибудь испытания в виде геометрической фигуры и свести вопрос о нахождении вероятности того или иного события к вычислению отношения площадей подходящих фигур. Таким способом можно решить еще несколько довольно известных задач — возможно, с некоторыми из них вы познакомитесь позже здесь, на «Элементах». Поэтому приведём в качестве упражнения лишь еще одну несложную задачу:

С какой вероятностью круглая монетка диаметра d, брошенная на клетчатую плоскость (разбитую на единичные квадратики), не покроет ни одну из линий сетки, то есть целиком окажется внутри какого-нибудь из квадратов?

Отметим, что, решая задачу Бюффона, можно рассуждать и немного иначе. Подробно ход такого решения описан (правда, на английском) здесь.

Теперь немного от том, в чём состоит смысл полученного нами ответа. При l = 1 ответ приблизительно равен 0,6366197. Что именно представляет это число? Как обычно, в теории вероятностей понимать это нужно следующим образом. Допустим, мы проделали очень длительную серию испытаний. Скажем, нам хватило терпения в каждом испытании бросать иголку миллион раз и запоминать, сколько раз она пересекла прямые линии на плоскости. И таких испытаний мы провели тоже миллион. Окажется, что в большинстве из них (скорее всего, подавляющем) число пересечений близко к 636 619. И чем больше мы будем проводить таких испытаний, тем ближе будет доля успешных исходов (когда иголка пересекла линию) к . И на самом деле, конечно, тут совершенно не важно, как подразделять испытания на серии — важно лишь общее количество. В реальности проводить такие длительные серии испытаний терпения не хватит. Но можно написать программу (или воспользоваться уже существующими типа этой), которая бы выполняла рутинные операции и выдавала только количество пересечений для большого числа бросков.

Сказанное в предыдущем абзаце даёт необычный подход к важной задаче точного вычисления числа π = 3,1415926. Напомним, что это число определяется как отношение длины окружности к её диаметру (для всех окружностей это отношение одинаково). Число π — одна из основных констант в математике и физике. Отчасти это можно пояснить тем, что окружности и эллипсы возникают в математике и физике в самых разных задачах и моделях — от чисто геометрических до практических вроде расчётов орбит планет и спутников. Поэтому важно уметь достаточно точно вычислять значение числа π. Известно, что это число иррациональное, то есть его нельзя представить в виде рациональной дроби (отношения двух целых чисел), но есть близкие к нему дроби с небольшими знаменателями. Еще Архимеду было известно, что дробь 22/7 = 3,(142 857) приближает π с точностью до тысячных. Примерно в V веке н. э. уже было известно приближение 355/113 = 3,14159292. — погрешность меньше одной миллионной.

При чём же здесь игла Бюффона? Как мы уже понимаем, в длительной серии испытаний доля пересечений от общего числа бросков иголки будет примерно равна 2/π. Поэтому мы можем эмпирически найти эту долю и вычислить приблизительное значение . Чем больше бросков, тем точнее будет доля, а значит, и значение π. В XIX веке находились герои, готовые потратить несколько вечеров на такое занятие. У них получались разные значения около 3,14. Подробнее можно прочитать на этой странице в английской Википедии.

Сейчас, конечно, никто иголку не бросает, а число π вычислено уже далеко за 10 триллионов знаков. Забавно, что такая точность и близко не нужна для практических вычислений — по оценкам, достаточно знать π примерно до 40-го знака после запятой, чтобы точно рассчитать объём видимой Вселенной с точностью до одного атома. Так что вычисление π с такой точностью — это, скорее, гонка за рекордами и соревнование суперкомпьютеров.

Точные вычисления основаны на разных формулах. В основном, используются сходящиеся к π последовательности и суммирование рядов, много алгоритмов можно найти в Википедии. Здесь приведём лишь замечательную формулу

которая позволяет вычислить любую цифру числа π, не вычисляя остальные цифры.

📸 Видео

7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

№201. Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Прямо пропорциональная и обратно пропорциональная зависимость. 6 класс.Скачать

ГЕОМЕТРИЯ 7 класс : Соответственные, односторонние и накрест лежащие углыСкачать

№160. Концы отрезка АВ лежат на двух параллельных плоскостях, расстояние междуСкачать

Следы прямойСкачать

ГЕОМЕТРИЯ 7 класс. Признаки параллельности, накрест лежащие, соответственные и односторонние углыСкачать

ЕГЭ Задание 11 Задача на движение протяженных телСкачать

Угол между прямыми в пространстве. Практическая часть. 10 класс.Скачать

УГЛЫ: Односторонние, Накрест Лежащие, Внутренние, Внешние // Теорема об углах — Геометрия 7 классСкачать

Теорема 14.1 Если накрест лежащие углы равны, то прямые параллельныСкачать

Сажина О. С. - Математическая обработка наблюдений - Теория вероятностей. Часть 2Скачать