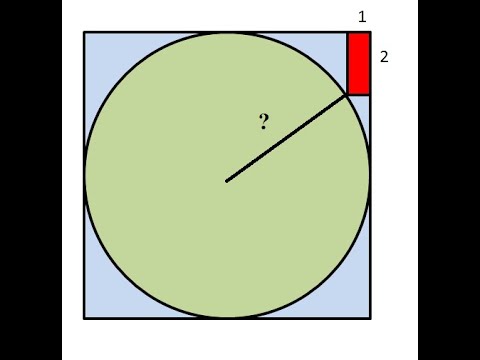
- Условие задачи:
- Найти площадь закрашенной области: S
- Ответ:
- Нахождение радиуса вписанной в квадрат окружности
- Формулы вычисления радиуса вписанной окружности
- Через сторону квадрата
- Через диагональ квадрата
- Примеры задач
- Радиусы описанной и вписанной окружностей в квадрат
- Окружность вписанная в квадрат
- Окружность описанная около квадрата
- Нахождения величины радиуса описанной окружности около квадрата при известной величине радиуса вписанной окружности.
- 📹 Видео
Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Условие задачи:
Окружность вписана в квадрат. Найти площадь закрашенной области, если сторона квадрата равна 2 м.
Дано:
Сторона квадрата, a = 2 м
Пояснение к рисунку:
O — центр окружности
R — радиус окружности
D — диаметр окружности
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Найти площадь закрашенной области: S
Площадь искомой области можно выразить как разницу между площадью квадрата и площадью круга
Неизвестен радиус окружности. Из рисунка видно, что сторона квадрата равна диаметру окружности и соответственно удвоенному радиусу
Выразим радиус окружности через сторону квадрата и подставив значение, получим радиус окружности.
Формула площади искомой области на основании выкладок выше, будет выглядеть следующим образом.
Подставив уже известные значения стороны квадрата и радиуса окружности, получаем.
Видео:ОПИСАННАЯ и ВПИСАННАЯ окружности. §21 геометрия 7 классСкачать

Ответ:
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Если в уже полученное выражение подставить формулу площади круга выраженную через сторону квадрата и преобразовав, получим следующую формулу, в которой площадь закрашенной области, будет сразу выражена через сторону квадрата.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Нахождение радиуса вписанной в квадрат окружности
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в квадрат. Также разберем примеры решения задач для закрепления теоретического материала.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Формулы вычисления радиуса вписанной окружности
Через сторону квадрата
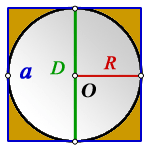
Радиус r вписанной в квадрат окружности равняется половине длины его стороны a.
Через диагональ квадрата
Радиус r вписанной в квадрат окружности равняется длине его диагонали d, деленной на произведение числа 2 и квадратного корня из двух.
Видео:Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Примеры задач
Задание 1
Найдите радиус вписанной в квадрат окружности, если известно, что длина его стороны равняется 7 см.
Воспользуемся первой формулой, подставив в него известное значение:
Задание 2
Известно, что радиус вписанной в квадрат окружности составляет 12 см. Найдите длину его диагонали.
Формулу для нахождения диагонали можно вывести из формулы для расчета радиуса круга:
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Радиусы описанной и вписанной окружностей в квадрат
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Окружность вписанная в квадрат
Чтобы формула нахождения радиуса вписанной окружности в квадрат r была правильно рассчитана, необходимо изначально вспомнить какими свойствами обладает данная фигура. 
- все углы прямые, то есть, равны 90°;
- все стороны, как и углы, равны;
- диагонали равны, точкой пересечения бьются строго пополам и пересекаются под углом 90°.
При этом вписанная в выпуклый многоугольник окружность обязательно касается всех его сторон. Обозначим квадрат ABCD, точку пресечения его диагоналей O. Как видно на рисунке 1, пересечение линий АС и ВD дают равнобедренный треугольник АОВ, в котором стороны АО=ОВ, углы ОАВ=АВО=45°, а угол АОВ=90°. Тогда радиусом вписанной окружности в квадрат будет не что иное, как высота ОЕ полученного равнобедренного треугольника АОВ.
Если предположить, что сторона квадрата равна у, то формула нахождения радиуса вписанной окружности в квадрат будет выглядеть следующим образом:
Объяснение: в равнобедренном треугольнике АОВ высота ОЕ или радиус r делят основание АВ пополам (свойства), образовывая при этом прямоугольный треугольник с прямым угол ОЕВ. В маленьком треугольнике ЕВО основание ОВ образует со сторонами ОЕ и ЕВ углы по 45°. Значит треугольник ЕВО еще и равнобедренный. Стороны ОЕ и ЕВ равны.
Видео:ОГЭ Площадь квадрата, описанного около окружности #огэ #огэ2023 #алгебра #огэматематикаСкачать

Окружность описанная около квадрата

Объяснение: после проведения диагоналей ABCD образовались два одинаковых прямоугольных треугольника АВС = CDA. Рассмотрим один из них. В треугольнике CAD:
- угол CDA=90°;
- стороны AD=CD. Признак равнобедренного треугольника;
- угол DAC равен ACD. Они равны по 45°.
Чтобы найти в этом прямоугольном треугольнике гипотенузу АС, необходимо воспользоваться теоремой Пифагора: 

Поскольку окружность касается вершин квадрата, а точка пересечения его диагоналей является центром описанной окружности (свойства), то отрезок ОС и будет радиусом окружности. Он является половинкой гипотенузы. Это утверждение вытекает из свойств равнобедренного треугольника или свойств диагоналей квадрата. Потому формула нахождения радиуса описанной окружности около квадрата в нашем случае имеет следующий вид: 
Поскольку AD=CD, а свойства квадратного корня позволяют вынести одно из подкоренных выражений, тогда формула приобретает вид:
Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

Нахождения величины радиуса описанной окружности около квадрата при известной величине радиуса вписанной окружности.
- треугольник ОСЕ – равнобедренный и прямоугольный;
- ОЕ=ЕС=
;
- ОЕС=90°;
- ЕОС=ОСЕ=45°;
Найти: ОС=?
Решение: в данном случае задачу можно решить, воспользовавшись либо теоремой Пифагора, либо формулой для R. Второй случай будет проще, поскольку формула для R выведена из теоремы.
📹 Видео
Задание 16 ОГЭ по математике. Окружность описана около квадратаСкачать

ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

17 задание ОГЭ по математикеСкачать

Урок 1. Вписанная и описанная окружность в квадратСкачать

Урок 2. Вписанная и описанная окружность в квадрат. Задача из ОГЭСкачать

СТОРОНА КВАДРАТА через РАДИУС вписанной и описанной окружностейСкачать

Вторая задача про вписанную окружность.Скачать
Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.Скачать

Найти площадь квадрата описанного около окружности радиуса 19Скачать



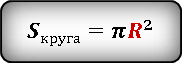
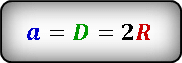
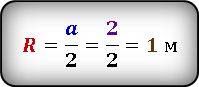

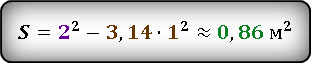








 ;
;