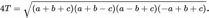Автор: Сагитова Елена[4],
ученица 7 класса
лицея № 19 г. Тольятти
Руководители: Утеева Р.А.,
Бабрышов Н.Г.
учитель математики высшей категории
лицея № 19 г. Тольятти
г. Тольятти, 1998.
Образец оформления введения
ВВЕДЕНИЕ
Основная цель работы: исследование
целочисленных прямоугольных треугольников.
Данная тема представляет определенный интерес, так как её истоки относятся к древности, так называемой знаменитой теореме Пифагора.
Основные задачи исследования:
1) познакомиться с понятием целочисленного прямоугольного треугольника;
2) выяснить, существуют ли целочисленные прямоугольные треугольники, гипотенузой которых является данное число n ( n £20);
3) выяснить, при каких условиях нечетное простое число является гипотенузой, а при каких – не является;
4) выяснить, какими могут быть значения катетов и гипотенузы целочисленных прямоугольных треугольников ( в смысле четности).
Основные методы решения поставленных задач: метод наблюдения за числами; метод
подбора и проб; чтение дополнительной литературы; составление таблиц и сравнение результатов; метод обобщения.
Образец оформления основной части работы
Часть 1. Основные понятия, используемые в работе
1.1. Понятие прямоугольного треугольника
Определение 1. Треугольник называется прямоугольным, если у него есть прямой угол. Стороны треугольника, образующие прямой угол называются катетами, а третья сторона, лежащая против прямого угла – гипотенузой.
Обычно длины катетов обозначают буквами a и b, длину гипотенузы – с, причем a + b >с.
1.2. Теорема Пифагора
Теорема: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов, т.е. с помощью обозначений эту теорему можно записать так: a 2 +b 2 = с 2 .
В настоящее время известно более 150 доказательств теоремы Пифагора, на которых мы не будем останавливаться, так как это не является предметом данной работы.
Отметим лишь, что эта теорема была известна в Древнем Вавилоне еще задолго до Пифагора (580-500 гг. до н.э.), примерно за 1000 лет.
По-видимому, её назвали именем древнегреческого математика Пифагора, так как согласно
легенде, он одним из первых доказал ее.
В геометрии также доказана и обратная теорема к теореме Пифагора: если длины сторон треугольника a , b и с удовлетворяют условию a 2 +b 2 = с 2 (1), то такой треугольник будет прямоугольным.
1.3. Понятие целочисленного прямоугольного треугольника
Треугольник со сторонами 3,4 и 5 является прямоугольным ( по обратной теореме Пифагора), так как удовлетворяет указанному выше условию (1). Такие треугольники называются целочисленными прямоугольными треугольниками. Некоторые такие треугольники были известны еще в Древнем Вавилоне и Египте, например, треугольники с длинами сторон 5,12 и 13; 17, 24 и 25.
Понятие целочисленного треугольника тесно связано с понятием диофантового уравнения, т.е. уравнения вида х 2 +y 2 =z 2 , которые также называются вавилонскими, а тройка чисел, удовлетворяющая этому уравнению, называется пифагоровой.
Часть 2. Постановка и решение задач
Исследования
2.1. Постановка первой задачи
Пусть дано, например. число n =12. Существует ли целочисленный прямоугольный треугольник с гипотенузой, равной 12?
Пусть х и у – катеты прямоугольного
треугольника и 0 2 +y 2 =12 2 или х 2 +y 2 =144.
Составим таблицу 1.
| х | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| х 2 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 |
| у 2 | 143 | 140 | 135 | 128 | 119 | 108 | 95 | 80 | 63 | 44 | 23 |
Из таблицы видно. что не существует целого значения у, значит не существует и целочисленного прямоугольного треугольника с гипотенузой, равной 12.
Ответ: не существует целочисленного
прямоугольного треугольника с длиной гипотенузы, равной 12.
Пусть теперь n =13. Тогда нам нужно
решить уравнение х 2 +y 2 =169.
Аналогично составим таблицу 2.
| х | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| х 2 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 |
| у 2 | 168 | 165 | 160 | 153 | 144 | 133 | 120 | 105 | 88 | 69 | 48 | 25 |
Из таблицы видно, что существует два
целых значения у: у=12 и у=5, значит с гипотенузой, равной 13, существует целочисленный прямоугольный треугольник с длинами сторон 5,12 и 13.
Для того чтобы и дальше не составлять
аналогичные таблицы, поступим по-другому. Так как по условию существования треугольника
х+у > n и, мы положили, что у £ х, значит
х 2 +y 2 £ 2х 2 , а 2х 2 ³ n 2 . Итак, 2х 2 ³169, отсюда находим, что х 2 ³84. Значит, достаточно проверить лишь три значения х 2 : 100, 121 и 144. Находим у 2 , из которых только одно значение целое. Это у=5 при х = 12.
Аналогично исследуем все остальные значения n (n £20). Результаты представим в виде
таблицы 3 ( Приложение). Ясно, что n ³3.
Треугольники со сторонами (3;4;5). (6;8;10), (9;12;15) подобны, поэтому в дальнейшем будем рассматривать только не подобные треугольники с гипотенузой n =5,13 и 17. Все эти числа оказались нечетными простыми числами.
Итак, сделаем первый вывод: существуют три ( не подобных) целочисленных прямоугольных треугольника с гипотенузой n, равной нечетному простому числу, где n£20.
2.2. Постановка второй задачи
При каких условиях нечетное простое число является гипотенузой, а при каких – не является?
Составим таблицу 4.
| нечетное простое число р | Прямоугольные треугольники с гипотенузой р |
| 3 | не существует |
| 5 | 25= 16+9 |
| 7 | не существует |
| 11 | не существует |
| 13 | 169 = 144 +25 |
| 17 | 289= 225+64 |
| 19 | не существует |
| 23 | не существует |
| 29 | 841= 441+400 |
| 31 | не существует |
Выпишем простые нечетные числа в два ряда и понаблюдаем за ними:
5, 13,17,29, … и 3,7,11,19,23,31, …
8 4 12 4 4 8 4 8
Итак, сделаем второй вывод: все разности делятся на 4, причем в первом случае остаток от деления простых чисел на 4 равен 1, а во втором -3.
Возникает гипотеза: простое число вида 4к+1 является гипотенузой, а простое число вида 4к+3 –не является. Проверим ее.
2.3. Теорема о примитивной
пифагоровой тройке
Определение 2. Пифагорову тройку чисел, в которой все числа взаимно просты, называют
примитивной.
Например, (3,4,5) –примитивная пифагорова тройка, а (6,8,10) –непримитивная.
Ясно, что в примитивной пифагоровой тройке два числа не могут быть четными ( тогда и третье число должно быть четным), но все они не могут одновременно быть нечетными.
Вывод: в примитивной пифагоровой тройке должно быть одно число четное, а два нечетных.
Замечание: 1. Надеемся, что на данном
примере мы смогли показать вам, как примерно можно представить результаты своего исследования.
Мы не стали здесь приводить всю работу целиком, а показали лишь, как можно оформить её.
Образец оформления заключения
Заключение
Проведенная выше работа позволила мне сделать следующие выводы:
1. Существует три ( не подобных) целочисленных прямоугольных треугольника с гипотенузой n ( n £20), равной нечетному простому числу. В общем случае, конечно их бесконечно много, так как доказано в математике, что простых чисел бесконечно много.
2. В целочисленных примитивных прямоугольных треугольниках только одна сторона
может быть выражена четным числом, остальные две стороны – нечетным.
3. В целочисленных примитивных прямоугольных треугольниках гипотенуза не может быть выражена четным числом.
4. Стороны целочисленного прямоугольного треугольника могут быть найдены по различным формулам. Вывод одной из них представлен в
работе.
списка использованной литературы
Литература:
1. Виленкин Н.Я., Шибасов Л.П., Шибасова З.Ф. За страницами учебника математики: Арифметика. Алгебра. Геометрия: Кн. для учащихся 10-11 классов общеобразоват. учрежд. – М., 1996. С. 83-87.
2. Дорофеева А.В. Страницы истории на уроках математики /Квантор.-1991.№6.С.33-35.
3. Пойа Дж. Математика и правдоподобные
рассуждения: перевод с анг. И.А. Вайнштейна /Под ред. С.А. Яновской. –Изд. 2-е.-М., 1975.С.80-82.
Елена Юрьевна Сагитова, студентка группы М 401
факультета математики и информатики ТГУ
Роза Азербаевна Утеева, доктор педагогических наук, профессор, зав.кафедрой алгебры и геометрии ТГУ
Видео:Что останется футбол или математика? Задача про треугольник с целочисленными сторонамиСкачать

Задача «Пифагоровы треугольники»
В теории чисел теорема Пифагора стала источником плодотворной идеи: найти целочисленные решения алгебраических уравнений.
Пифагорова тройка — это набор целых чисел a, b и c, таких что: a 2 + b 2 = c 2 . Геометрически такая тройка определяет прямоугольный треугольник с целочисленными сторонами. Самая маленькая гипотенуза пифагоровой тройки равна 5. Другие две стороны этого треугольника равны 3 и 4. Здесь 3 2 + 4 2 = 9 + 16 = 25 = 5 2 .
Пифагоров треугольник с этими сторонами известен с глубокой древности. Он называется египетским, и использовался для построения прямого угла на местности. Вместо вычерчивания применялась верёвка, разделённая 12 узлами на равные части, которая натягивалась на 3 колышка.
Пифагорова тройка (a, b, c) называется примитивной, если она не может быть получена делением всех сторон на целое число из какой-то другой пифагоровой тройки, то есть если (a , b , c) являются взаимно простыми числами. Другими словами, наибольший общий делитель (НОД) примитивной пифагоровой тройки ( a, b, c ) равен 1.
Как вы думаете, много ли найдется таких троек?
Постановка задачи
Требуется найти все примитивные тройки, для которых длина катетов не превышает некоторого заданного числа k, упорядочить тройки по возрастанию площади соответствующих треугольников, вывести их на печать и подсчитать общее число таких троек.
Алгоритм решения
Создадим структуру pif1 c полями a, b,c, s и методом print_P(). Инициализируем массив pif3 , элементами которого будут структуры pif1.
Для поиска (метод static int poisk3(int k)) будем используем прямой перебор и два цикла. В первом цикле a изменяется от 3 до k, а во втором (внутреннем) цикле b изменяется от 4 до k. Если гипотенуза такого треугольника является целым числом, то вычисляется его площадь s, и такой треугольник запоминается в массив pif3.
После этого выполняется упорядочивание массива по возрастанию (по полю s, метод sort3(n)). Очевидно, что сортировка может быть выполнена по любому другому полю, например по гипотенузе с.
При выводе троек (метод output3(n) c использованием print_P() ) выводятся только те, у которых НОД=1 (дважды применяется метод «Наибольший общий делитель» nod(x, y) ).
Максимальная длина катетов задается первыми двумя операторами метода Main(), после чего выполняется поиск, сортировка и вывод результатов.
Программная реализация
Результат 
Задание
Исследуйте, как изменяется результат в зависимости от максимальной длины катета k. Обратите внимание на время решения задачи T (используйте секундомер). Является ли зависимость T=f (k) линейной, т.е. действительно ли T
Перейдем к следующей задаче — формированию массива простых чисел.
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Проект по математике на тему:»Треугольники с целочисленными сторонами».
Проект по математике на тему:»Треугольники с целочисленными сторонами».
Просмотр содержимого документа
«Проект по математике на тему:»Треугольники с целочисленными сторонами».»
ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ПАЛЛАСОВСКИЙ СЕЛЬСКОХОЗЯЙСТВЕННЫЙ ТЕХНИКУМ»
Тема проекта: «Треугольники с целочисленными сторонами»
Работу выполнил: Кривоногих Константин Алексеевич /_________/
Группа 1МСХ9 специальность Механизация сельского хозяйства
Дисциплина Математика: алгебра и начала математического анализа; геометрия
Преподаватель: Низамова Гульнара Ахмедовна /_________/
Оценка за проект________________________
1. Основные свойства целых треугольников………………………………. 5
3. Целочисленные треугольники на двумерной решетке………………. 10
Список использованной литературы……………………………………..…….14
Целочисленный треугольник — это треугольник, длины всех сторон которого выражаются целыми числами. Рациональный треугольник можно определить, как треугольник, стороны которого являются рациональными числами. Любой рациональный треугольник можно привести к целочисленному (умножив все стороны на одно и тоже число, наименьшее общее кратное знаменателей), так что нет существенной разницы между целочисленными и рациональными треугольниками.
Актуальность данной темы заключается в том, что полученные при исследовании целочисленных треугольников результаты будут интересны как специалистам в области элементарной геометрии, так и учащимся выпускных классов при поиске нестандартных способов и методов решения задач, связанных с теорией целых чисел.
Объект исследования: треугольники.
Предмет исследования треугольники с целочисленными сторонами.
Цель: доказать, что сложные треугольники Герона состоят из двух компонентных треугольников Пифагора, или из них исходящих, других не существует (задача).
Для достижения поставленной цели мною были определены следующие задачи:
рассмотреть основные свойства целых треугольников;
изучить треугольники Герона целочисленные треугольники на двумерной решетке
рассмотреть целочисленные треугольники со специфичными свойствами углов и целочисленные треугольники с целым отношением радиусов описанного и вписанного окружностей.
В процессе выполнения работы мною были использованы следующие методы исследования:
-изучение и анализ научную литературу;
-обобщение изученной информации;
Данная работа состоит из введения, основной части, списка использованной литературы.
1. Основные свойства целых треугольников
Целочисленные треугольники с заданным периметром.
Любая тройка положительных чисел может стать сторонами треугольника, необходимо лишь удовлетворение неравенства треугольника — самая длинная сторона должна быть короче суммы двух других сторон. Каждая такая тройка задаёт единственный (с точностью до конгруэнтности) треугольник. Так что число целочисленных треугольников с периметром p равно числу разбиений p на три положительные части, удовлетворяющие неравенству треугольника. Эти числа являются ближайшими к p 2 48 для чётных p и к (p + 3) 2 48 для нечётных. Это также означает, что число целочисленных треугольников с чётным периметром p = 2 n равно числу с нечётным периметром p = 2n — 3. Таким образом, нет треугольников с периметрами 1, 2 и 4, имеется по одному с периметрами 3, 5, 6 и 8, и по два с периметрами 7 и10. Последовательность числа целочисленных треугольников с периметрами p, начиная с p = 1:
0, 0, 1, 0, 1, 1, 2, 1, 3, 2, 4, 3, 5, 4, 7, 5, 8, 7, 10, 8… (последовательность А00504 и OEIS).
Целочисленные треугольники с заданной большей стороной.
Число целочисленных треугольников (с точностью до конгруэнции) с заданной наибольшей стороной c равно числу троек (a, b, c), таких, что a + b c и a ≤ b ≤ c. Это значение равно Ceiling[(c + 1)⁄2] * Floor[(c + 1)⁄2]. Для чётных c это равно удвоенному треугольному углу c⁄2(c⁄2 + 1), а для нечётных c это равно квадрату (c + 1)2⁄4. Это означает, что число целочисленных треугольников с наибольшей стороной c превышает число целочисленных треугольников с наибольшей стороной c−2 на c.
Последовательность числа неконгруэнтных целочисленных треугольников с наибольшей стороной, начиная с c = 1:
1, 2, 4, 6, 9, 12, 16, 20, 25, 30, 36, 42, 49, 56, 64, 72, 81, 90 … (последовательностьA002620 OEIS)
Число целочисленных треугольников (с точностью до конгруэнции) с данной наибольшей стороной c, вершины которого лежат на или внутри полуокружности диаметра c, равно числу троек (a, b, c), таких, что a + b c , a2 + b2 ≤ c2 и a ≤ b ≤ c. Это число совпадает с числом целочисленных треугольников с тупым или прямым углом с наибольшей стороной c. Последовательность числа таких треугольников, начинающаяся с c = 1:0, 0, 1, 1, 3, 4, 5, 7, 10, 13, 15, 17, 22, 25, 30, 33, 38, 42, 48 … (последовательность А236384 OEIS)
Разница между последними двумя последовательностями даёт число целочисленных треугольников с острыми углами (с точностью до конгруэнции) с наибольшей стороной c. Последовательность числа остроугольных треугольников, начиная с c = 1:
1, 2, 3, 5, 6, 8, 11, 13, 15, 17, 21, 25, 27, 31, 34, 39, 43, 48, 52 … (последовательность А247588 в OEIS)
Площадь целочисленного треугольника
По формуле Герона, если T — площадь треугольника, а длины стороны равны a, b и c, то
Поскольку все множители под знаком корня в правой части формулы являются целыми числами, все целочисленные треугольники должны иметь целочисленное значение величины16T2.
Углы целочисленного треугольника
По теореме косинусов любой угол целочисленного треугольника имеет рациональный косинус. Если углы любого треугольника образуют арифметическую прогрессию, то один из его углов должен быть 60°. Для целочисленных треугольников оставшиеся углы должны также иметь рациональные косинусы и метод генерации таких треугольников приведён ниже. Однако, за исключением тривиального случая равностороннего треугольника, не существует целочисленных треугольников, углы которого образуют геометрическую или гармоническую прогрессию. Это потому, что углы должны быть рациональными углами вида πp q с рациональными 0
Деление стороны высотой
Любая высота, опущенная из вершины на противоположную сторону или её продолжение, делит эту сторону (или продолжение) на отрезки рациональной длины.
🔍 Видео
Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Задача, которой русские школьники мучали американскихСкачать

Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Математика. Линейные диофантовы уравнения с двумя неизвестными. Центр онлайн-обучения «Фоксфорд»Скачать

Найдите площадь треугольника изображенного на клетчатой бумаге с размером клетки 1х1 см.Скачать

Задача, которая ставит в тупик 90 школьниковСкачать

Классический способ решения Диофантовых уравнений ➜ Решите уравнение в целых числах ➜ 13x-7y=6Скачать

Найдите угол: задача по геометрииСкачать

Математика это не ИсламСкачать

9 класс, 15 урок, Решение треугольниковСкачать

Метод ГомориСкачать

Решение задач с целочисленным ответом. Подготовка к ЕГЭ по математике #7Скачать

Целочисленное программирование Метод ветвей и границСкачать

Задание 3 ЕГЭ по математике. Урок 11Скачать

Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Визуализация всех возможных пифагоровых троек [3Blue1Brown]Скачать
![Визуализация всех возможных пифагоровых троек [3Blue1Brown]](https://i.ytimg.com/vi/T0GOz-Eqxl4/0.jpg)
Найдите стороны треугольникаСкачать

Решение задач с целочисленным ответом на расчет, оценку и прикидку. ГВЭ + ЕГЭ 2021 по математике #7Скачать