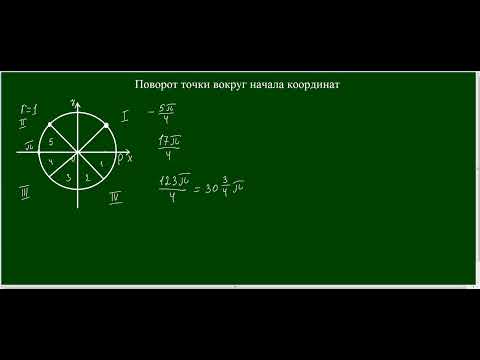Поворот точки на единичной окружности отрицательный положительный

Среди множества терминов тригонометрии важным является понятие угла поворота. В данной статье рассмотрим поворот и все соответствующие ему определения; дадим представление о полном обороте; изучим угол поворота и его характеристики, а также поворот фигуры вокруг точки. Для лучшего понимания теория будет снабжена иллюстрациями и практическими примерами.

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Поворот точки вокруг точки

Центр поворота – точка, относительно которой осуществлен поворот.

Рассмотрим, что происходит в результате поворота точки. Пусть некоторая точка А поворачивается относительно центра поворота О , в результате чего получается точка А 1 (при совершении некоторого количества полных оборотов она может совпасть с точкой А ). При этом точка А 1 лежит на окружности с центром в точке О радиуса О А . Другими словами, когда точка А осуществляет поворот относительно точки О , она переходит в точку А 1 , лежащую на окружности с центром О радиуса О А .

Считается, что в данном случае точка О при осуществлении поворота вокруг самой себя переходит в саму себя. Или: когда точка О осуществляет поворот вокруг центра поворота О , она переходит в саму себя.

Отметим также, что поворот точки А относительно центра О нужно рассматривать, в том числе, как перемещение в результате движения точки А по окружности с центром в точке О радиуса О А .

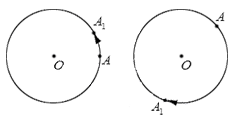
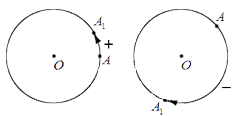
Изобразим графически поворот точки А относительно точки О , перемещение точки А в точку А 1 отметим стрелкой:

Видео:Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Полный оборот

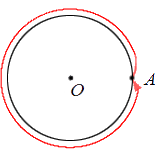
Возможно осуществить поворот точки А относительно центра поворота О таким образом, что точка А , пройдя все точки окружности, вернется на прежнее свое место. Тогда говорим, что точка совершила полный оборот вокруг точки О .

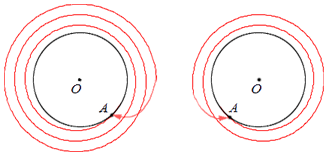
Если движение точки А по окружности продолжится, то будет выполнено два, три и так далее полных оборотов. На иллюстрации ниже справа отображено два полных оборота, а слева – три:

В рамках всего вышесказанного можно также говорить о частях полного оборота. Например, о половине оборота или трети, или четверти и так далее.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Угол поворота

Из указанного выше понятия поворота точки очевидно, что возможно бесконечное множество вариаций поворота точки А относительно центра О . Любую точку окружности с центром О можно рассматривать как точку А 1 , полученную в результате поворота точки А . Поэтому для определения отличия одного поворота от другого вводится понятие угла поворота.

Угол поворота имеет свои характеристики, одна из которых – направление поворота. По нему определяют, как перемещалась точка – по часовой стрелке или против.

Еще одной характеристикой угла поворота служит его величина. Углы поворота имеют ту же единицу измерения, что и углы в геометрии: наиболее распространены градусы и радианы. Отметим, что угол поворота может выражаться в градусах любым действительным числом в промежутке от — ∞ до + ∞ , что отличает его от угла в геометрии, который выражается только положительным числом, не превосходящим 180 ° .

Чтобы обозначить углы поворота, стандартно используют буквы греческого алфавита: α , β , γ и так далее. Чтобы обозначить большое количество углов поворота, применяют одну и ту же букву с различными нижними индексами: α 1 , α 2 , α 3 … . . α n .

Разберем характеристики угла поворота подробнее.

Видео:Найти координаты точки единичной окружности полученной при повороте точки Ро(1;0) на угол π, 450°...Скачать

Направление поворота

Отметим на окружности с центром О точки А и А 1 . В точку А 1 возможно попасть, совершив точкой А поворот относительно центра О либо по часовой стрелке, либо – против. Очевидно определять эти повороты, как различные.

Принято считать, что поворот по часовой стрелке – поворот в отрицательном направлении направлении, а поворот против часовой стрелки – поворот в положительном направлении.

Приведем графическую иллюстрацию различных поворотов: слева на чертеже – поворот в положительном направлении; справа – в отрицательном.

Видео:Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать

Величина угла поворота, угол произвольной величины

Угол поворота точки, не являющейся центром поворота, в полной мере определяется указанием его величины. С другой стороны, по величине угла поворота можно определить, каким образом поворот был осуществлен.

Как было сказано выше, величина угла поворота варьируется в пределах от — ∞ до + ∞ ;

Знак плюс определяет поворот против часовой стрелки, а минус – по часовой стрелке.

Необходимо установить соответствие между самой величиной угла поворота и тем, какому повороту она соответствует.

Пусть угол поворота равен 0 ° . Такому углу поворота соответствует перемещение точки в саму себя. Иначе говоря, при повороте вокруг точки О на 0 ° точка A остается на месте.

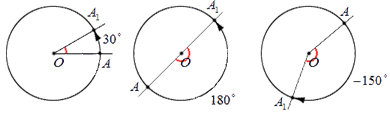
Теперь предположим, что поворот точки А происходит в пределах половины оборота: пусть точка А переходит в точку А 1 . В таком случае абсолютная величина угла А О А 1 , выраженная в градусах, не превосходит 180 . Если поворот имел положительное направление, то величина угла поворота считается равной величине угла А О А 1 ; если отрицательное – величина угла поворота равна величине угла А О А 1 со знаком минус. Для иллюстрации этих утверждений отобразим на чертеже углы поворота в 30 ° , 180 ° и — 150 ° :

Углы поворота, превышающие 180 или меньшие – 180 определяются, исходя из очевидного свойства последовательных поворотов:

Несколько последовательных поворотов точки А относительно центра О равносильны одному повороту, величина которого равна сумме величин этих поворотов.

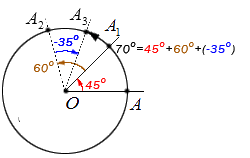
Рассмотрим пример, который даст нам возможность графически проиллюстрировать описанное свойство. Пусть точка А выполняет поворот относительно центра О на 45 ° , затем еще на 60 ° и еще раз — на — 35 ° . Обозначим промежуточные точки поворотов А 1 , А 2 и А 3 . В конечную точку А 3 возможно было попасть, совершив один поворот на угол поворота, величина которого равна: 45 ° + 60 ° + ( — 35 ° ) = 70 ° . Проиллюстрируем:

Таким, образом, углы, превышающие 180 ° , будем представлять, как несколько последовательных поворотов на углы, сумма величин которых определяет величину исходного угла поворота. Например, угол поворота 298 ° соответствует последовательным поворотам на 180 ° и 118 ° , или 90 ° , 90 ° , 90 ° и 28 ° , или 180 ° , 180 ° и — 62 ° , или 298 последовательных поворотов на 1 ° .

По такому же принципу определяются углы меньше — 180 ° . Например, угол поворота — 515 ° можно определить, как последовательные повороты на — 180 ° , — 180 ° и — 155 ° .

Нами был определен угол поворота, и его величина выражается в градусах некоторым действительным числом в пределах от — ∞ до + ∞ . Тригонометрия работает именно с углами поворота, хотя для удобства слово «поворот» опускают и говорят «угол». Т.е. будем рассматривать углы произвольной величины, понимая под ними углы поворота.

В заключение также отметим, что полный оборот в положительном направлении соответствует углу поворота в 360 ° или 2 π радиан. Соответственно при отрицательном направлении полный оборот будет соответствовать углу в — 360 ° или — 2 π радиан.

При этом удобно большие углы поворота представлять, как некоторое количество полных оборотов и еще один на величину в пределах от — 180 ° до 180 ° . К примеру, поворот осуществляется на 1478 ° . Представим эту величину как: 360 · 4 + 38 , т.е. заданному углу поворота соответствуют 4 полных оборота и еще один поворот – на 38 ° . Или еще один пример: угол поворота в — 815 ° можно представить, как ( — 360 ) · 2 + ( — 95 ) , т.е. заданному углу поворота соответствуют 2 полных оборота в отрицательном направлении (против часовой стрелки) и еще один поворот того же направления на — 95 ° .

Видео:Как искать точки на тригонометрической окружности.Скачать

Поворот фигуры вокруг точки на угол

Понятие поворота точки легко распространить на поворот любой фигуры вокруг точки на угол (такой поворот, при котором и точка, относительно которой осуществляется поворот, и сама поворачиваемая фигура лежат в одной плоскости).

Поворот фигуры – это поворот всех ее точек вокруг заданной точки на заданный угол.

Как пример, иллюстрируем следующее действие: поворот отрезка А В на угол α относительно точки О – при повороте заданный отрезок перейдет в отрезок А 1 В 1 .

Видео:Решение задач по теме "Поворот точки вокруг начала координат"Скачать

Алгебра

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Видео:Тригонометрическая окружность. Как выучить?Скачать

Числовая и единичная окружность

В средней школе мы уже познакомились с координатной, или числовой прямой. Так называют абстрактную прямую, на которой выбрана точка отсчета, определен единичный отрезок, а также задано направление, в котором следует откладывать положительные числа. С помощью координатной прямой удается наглядно представлять сложение и вычитание как положительных, так и отрицательных чисел, решать задачи, связанные с перемещением по прямой, и делать многое другое.

Однако порою приходится рассматривать задачи, связанные с движением по окружности, а также складывать и вычитать углы. Здесь математикам помогает другая абстракция – числовая окружность. Пусть два гонщика (Вася и Петя) едут по круговой трассе, чья протяженность составляет 1 км. За минуту Вася проехал 1250 м, а Петя преодолел только 500 м. Попытаемся показать их положение графически.

Построим на координатной плоскости окружность с центром в начале координат длиной 1 км. Будем считать, старт находится в крайней правой точке трассы, на пересечении оси Ох и окружности. Также условимся, что гонщики едут против часовой стрелки. Тогда получим такую картинку:

Петя проедет ровно половину окружности и окажется в крайней левой точке трассы. Вася же за минуту успел сделать полный круг (1 км) и проехать ещё 250 м, а потому оказался в верхней точке.

Теперь предположим, что Петя стоит на месте, а Вася проехал ещё 250 м (четверть круга). В результате оба пилота оказались в одной точке, но проехали они разное расстояние! Получается, что по положению гонщика невозможно однозначно определить, сколько именно метров он проехал.

Заметим, что очень удобно характеризовать положение точки на числовой окружности с помощью угла. Достаточно соединить точку отрезком с началом координат. Полученный отрезок образует с прямой Ох некоторый угол α:

В тригонометрии предпочитают использовать особую числовую прямую, радиус которой равен единице. По ряду причин, которые станут ясны чуть позже, с ней очень удобно работать. Такую фигуру называют единичной окружностью.

Выглядит единичная окружность так:

Видео:§22 Поворот точки вокруг начала координатСкачать

Откладывание углов на единичной окружности

Положение каждой точки на единичной окружности можно указать с помощью угла. Пусть надо найти точку, соответствующую углу 60°. Для этого просто строим угол следующим образом:

Углы, которые откладывают на единичной окружности, называют углами поворота. В данном случае можно утверждать, что точке А соответствует угол поворота, равный 60°.

Отложить можно и угол, больший 90° и даже 180°. Выглядеть они будут примерно так:

Углы можно складывать друг с другом и вычитать. Предположим, нам надо построить угол, равный сумме углов 120° и 110°. Для этого сначала совершить поворот на 120°, а потом от полученного отрезка отложить ещё один угол в 110°:

Ясно, что возможно построить любой угол в диапазоне от 0° до 360°. А можно ли отложить угол, который будет больше 360°? В обычной планиметрии мы не работаем с такими углами, однако в тригонометрии они существуют. Действительно, мы же можем, например, сложить углы 250° и 140°. В итоге получится 250 + 140 = 390°:

В результате мы совершили полный оборот (360°) и вдобавок повернули отрезок ещё на 30°. Получается, что углам в 390° и 30° соответствует одна и та же точка.

Углы можно и вычитать друг из друга. Для этого вычитаемый угол надо отложить в противоположном направлении – не против часовой, а по часовой стрелке. Например, вычитая из 150° угол в 70°, придем в точку, соответствующую 150 – 70 = 80°:

Из арифметики мы помним, что вычитание можно заменить прибавлением противоположного (то есть отрицательного) числа:

Получается, что отложив угол 70° по часовой стрелке, мы прибавили к 150° отрицательный угол (– 70°). То есть на единичной окружности можно откладывать отрицательные углы! Для их получения поворот надо осуществлять по часовой стрелке. Например, угол – 60° будет выглядеть так:

Итак, мы можем откладывать и положительные, и отрицательные углы, а также углы, большие 360°. Вообще в тригонометрии угол может быть равен любому действительному числу. На единичной окружности можно отложить углы величиной 1000°, 1000000° и (– 999999999°) и любые другие, самые большие и самые малые углы. В этом смысле единичная окружность схожа с координатной прямой. Разница лишь в том, что на прямой разным числам всегда соответствуют разные точки, а на окружности разным углам могут соответствовать одни и те же точки.

Ещё раз отметим, что один полный оборот равен 360°. Если отложить на окружности произвольную точку А, которой соответствует угол α, а потом добавить к α ещё 360°, то мы попадем в ту же самую точку:

С точки зрения тригонометрии те углы поворота, которые соответствуют одной точке на единичной окружности, равны друг другу. Поэтому можно записать формулу:

Естественно, при вычитании 360° из угла мы тоже совершим полный поворот, только по часовой стрелке, поэтому верна и другая запись:

Угол, не изменится и в том случае, если мы совершим не один, а два полных оборота, то есть добавим к нему 2•360° = 720°. Можно добавлять к углу два, три, четыре полных поворота, но он не изменится от этого. Обозначим буквой n количество оборотов, которые мы добавляем к углу. Естественно, что n – целое число. Справедливой будет формула:

Например, верны следующие равенства:

15° + 3•360° = 15° + 1080° = 1095°

100° + 10•360° = 100° + 3600° = 3700°

1000° = 1000° – 2•360° = 1000° – 720° = 280°

Очевидно, что любой точке на окружности соответствует какой-то угол α из промежутка 0 ≤ α 1 5

Видео:Алгебра 10 класс Поворот точки вокруг начала координат СеминарСкачать

Угол поворота, угол произвольной величины.

В тригонометрии важным понятием является угол поворота. Ниже мы последовательно будем давать представление о повороте, и вводить все сопутствующие понятия. Начнем с общего представления о повороте, скажем о полном обороте. Далее перейдем к понятию угла поворота и рассмотрим его основные характеристики, такие как направление и величина поворота. Наконец, дадим определение поворота фигуры вокруг точки. Всю теорию по тексту будем снабжать поясняющими примерами и графическими иллюстрациями.

Навигация по странице.

Видео:В какой четверти находится точка единичной окружности, полученная при повороте Ро(1;0) на угол...Скачать

Что называют поворотом точки вокруг точки?

Сразу отметим, что наряду с фразой «поворот вокруг точки» будем также использовать словосочетания «поворот около точки» и «поворот относительно точки», что обозначает одно и то же.

Введем понятие поворота точки вокруг точки.

Сначала дадим определение центра поворота.

Точку, относительно которой осуществляется поворот, называют центром поворота.

Теперь скажем, что получается в результате поворота точки.

В результате поворота некоторой точки A относительно центра поворота O получается точка A₁ (которая в случае некоторого количества полных оборотов может совпадать с A ), причем точка A₁ лежит на окружности с центром в точке O радиуса OA . Иными словами, при повороте относительно точки O точка A переходит в точку A₁ , лежащую на окружности с центром в точке O радиуса OA .

Считают, что точка O при повороте вокруг самой себя переходит в саму себя. То есть, в результате поворота вокруг центра поворота O точка O переходит в саму себя.

Также стоит отметить, что поворот точки А вокруг точки O стоит рассматривать как перемещение в результате движения точки А по окружности с центром в точке O радиуса OA .

Для наглядности приведем иллюстрации поворота точки А вокруг точки O , на рисунках, расположенных ниже, перемещение точки А в точку А₁ покажем при помощи стрелки.

Видео:Изобразить на единичной окружности точку.Скачать

Полный оборот

Можно выполнить такой поворот точки A относительно центра поворота O , что точка А , пройдя все точки окружности, окажется на прежнем месте. При этом говорят, что точка А совершила полный оборот вокруг точки O .

Дадим графическую иллюстрацию полного оборота.

Если же не останавливаться на одном обороте, а продолжать движение точки по окружности, то можно выполнить два, три и так далее полных оборотов. На чертеже ниже справа показано, как могут быть произведены два полных оборота, а слева — три оборота.

Можно также говорить о частях полного оборота, например, о половине оборота, трети, четверти и т.д. оборота (при надобности смотрите статью доли и обыкновенные дроби).

Видео:Как найти координаты точек на тригонометрической окружностиСкачать

Понятие угла поворота

Из введенного в первом пункте понятия поворота точки понятно, что существует бесконечное множество вариантов поворота точки А вокруг точки O . Действительно, любую точку окружности с центром в точке O радиуса OA можно рассматривать как точку A₁ , полученную в результате поворота точки А . Поэтому, чтобы отличать один поворот от другого, вводится понятие угла поворота.

Одной из характеристик угла поворота является направление поворота. По направлению поворота судят о том, как осуществляется поворот точки – по часовой стрелке или против часовой стрелки.

Другой характеристикой угла поворота является его величина. Углы поворота измеряются в тех же единицах, что и углы в геометрии: наиболее распространены градусы и радианы. Здесь стоит заметить, что угол поворота может выражаться в градусах любым действительным числом из промежутка от минус бесконечности до плюс бесконечности, в отличие от угла в геометрии, величина которого в градусах положительна и не превосходит 180 .

Для обозначения углов поворота обычно используются строчные буквы греческого алфавита: и т.д. Для обозначения большого количества углов поворота часто применяют одну букву с нижними индексами, к примеру, .

Теперь поговорим о характеристиках угла поворота подробнее и по порядку.

Направление поворота

Пусть на окружности с центром в точке O отмечены точки A и A₁ . В точку А₁ можно попасть из точки A , выполнив поворот вокруг центра O либо по часовой стрелке, либо — против часовой стрелки. Эти повороты логично считать различными.

Условились считать поворотом в положительном направлении такой поворот, который осуществляется против хода часовой стрелки. Поворот по часовой стрелке называют поворотом в отрицательном направлении.

Проиллюстрируем повороты в положительном и отрицательном направлении. На чертеже ниже слева показан поворот в положительном направлении, а справа – в отрицательном.

Величина угла поворота, угол произвольной величины

Угол поворота точки, отличной от центра поворота, полностью определяется указанием его величины, с другой стороны, по величине угла поворота можно судить о том, как этот поворот был осуществлен.

Как мы уже упоминали выше, величина угла поворота в градусах выражается числом от −∞ до +∞ . При этом знак плюс соответствует повороту по часовой стрелке, а знак минус – повороту против часовой стрелки.

Теперь осталось установить соответствие между величиной угла поворота и тем, какому повороту она соответствует.

Начнем с угла поворота, равного нулю градусам. Этому углу поворота отвечает перемещение точки А в себя. Другими словами, при повороте на 0 градусов вокруг точки O точка А остается на месте.

Переходим к повороту точки А вокруг точки O , при котором поворот происходит в пределах половины оборота. Будем считать, что точка А переходит в точку А₁ . В этом случае абсолютная величина угла AOA₁ в градусах не превосходит 180 . Если поворот происходил в положительном направлении, то величина угла поворота считается равной величине угла AOA₁ , а если поворот происходил в отрицательном направлении, то его величина считается равной величине угла АОА₁ со знаком минус. Для примера приведем рисунок, показывающий углы поворота в 30 , 180 и −150 градусов.

Углы поворота большие 180 градусов и меньшие −180 градусов определяются на основе следующего достаточно очевидного свойства последовательных поворотов: несколько последовательных поворотов точки A вокруг центра O равносильны одному повороту, величина которого равна сумме величин этих поворотов.

Приведем пример, иллюстрирующий данное свойство. Выполним поворот точки А относительно точки O на 45 градусов, а затем еще повернем эту точку на 60 градусов, после чего повернем эту точку на −35 градусов. Обозначим промежуточные точки при этих поворотах как A₁ , A₂ и A₃ . В эту же точку А₃ мы могли попасть, выполнив один поворот точки A на угол 45+60+(−35)=70 градусов.

Итак, углы поворота, большие 180 градусов, мы будем представлять как несколько последовательных поворотов на углы, сумма величин которых дает величину исходного угла поворота. Например, угол поворота 279 градусов соответствует последовательным поворотам на 180 и 99 градусов, или на 90 , 90 , 90 и 9 градусов, или на 180 , 180 и −81 градус, или на 279 последовательных поворотов по 1 градусу.

Аналогично определяются и углы поворота, меньшие −180 градусов. К примеру, угол поворота −520 градусов можно интерпретировать как последовательные повороты точки на −180 , −180 и −160 градусов.

Подведем итог. Мы определили угол поворота, величина которого в градусах выражается некоторым действительным числом из промежутка от −∞ до +∞ . В тригонометрии мы будем работать именно с углами поворота, хотя слово «поворот» часто опускают, и говорят просто «угол». Таким образом, в тригонометрии мы будем работать с углами произвольной величины, под которыми будем понимать углы поворота.

В заключение этого пункта отметим, что полный оборот в положительном направлении соответствует углу поворота в 360 градусов (или 2·π радианов), а в отрицательном – углу поворота в −360 градусов (или −2·π рад). При этом удобно большие углы поворота представлять как некоторое количество полных оборотов и еще один поворот на угол величиной от −180 до 180 градусов. Для примера возьмем угол поворота 1 340 градусов. Несложно 1 340 представить как 360·4+(−100) . То есть, исходному углу поворота отвечают 4 полных оборота в положительном направлении и последующий поворот на −100 градусов. Другой пример: угол поворота −745 градусов можно интерпретировать как два оборота против часовой стрелки и последующий поворот на −25 градусов, так как −745=(−360)·2+(−25) .

Видео:Радианная мера угла. 9 класс.Скачать

Поворот фигуры вокруг точки на угол

Понятие поворота точки легко расширяется на поворот любой фигуры вокруг точки на угол (речь идет о таком повороте, что и точка, относительно которой осуществляется поворот, и фигура, которую поворачивают, лежат в одной плоскости).

Под поворотом фигуры будем понимать поворот всех точек фигуры вокруг заданной точки на данный угол.

В качестве примера приведем иллюстрацию следующему действию: выполним поворот отрезка AB на угол относительно точки O , это отрезок при повороте перейдет в отрезок A₁B₁ .

🔥 Видео

Поворот точки вокруг начала координатСкачать

Точки, полученные поворотом точки Р (1; 0) вокруг начала координат на заданные углыСкачать

Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

поворот точки вокруг начала координат 10 класс алгебра и анализСкачать

Алгебра 10 класс (Урок№29 - Радианная мера угла.)Скачать

Поворот точки вокруг начала координатСкачать