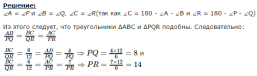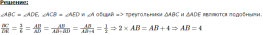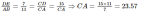Представлены задачи по теме Подобие треугольников:
1) для самостоятельного решения; 2) с решениями; 3) из сборника ОГЭ; 4) тест.
- Просмотр содержимого документа «Решение задач по теме «Подобие треугольников»»
- Задачи с практическим содержанием по теме «Подобие треугольников»
- Задачи наподобие треугольников повышенной сложности
- Урок 36. Решение задач на применение признаков подобия треугольников
- I. Организационный момент.
- II. Актуализация знаний учащихся
- III. Самостоятельная работа
- I уровень сложности
- II уровень сложности
- III уровень сложности
- IV. Рефлексия учебной деятельности
- 🌟 Видео
Просмотр содержимого документа
«Решение задач по теме «Подобие треугольников»»
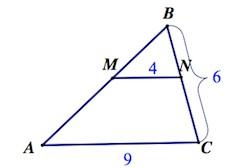
1. Через точки М и N, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая МN, параллельная стороне АС. Найдите длину СN, если ВС = 6, МN = 4, АС = 9.
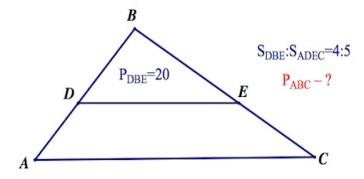
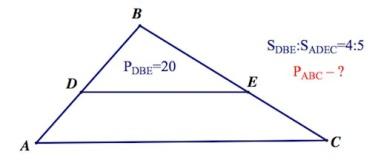
2. Прямая, параллельная основанию треугольника, делит его на треугольник и трапецию, площади которых относятся как 4:5. Периметр образовавшегося треугольника равен 20 см. Найдите периметр данного треугольника.
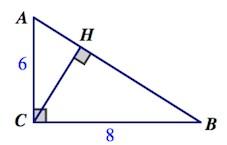
3. Через вершину прямого угла прямоугольного треугольника с катетами 6 и 8 см проведен перпендикуляр к гипотенузе. Вычислите площади образовавшихся треугольников.
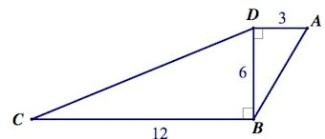
4. В трапеции ABCD меньшая диагональ BD, равная 6, перпендикулярна основаниям AD=3 и DC=12. Найдите сумму тупых углов B и D.
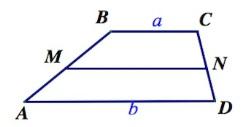
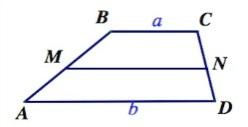
5. Основания трапеции равны a и b. Определите длину отрезка, параллельного основаниям и делящего трапецию на равновеликие части.
1. Через точки М и N, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая МN, параллельная стороне АС. Найдите длину СN, если ВС = 6, МN = 4, АС = 9.
2. Прямая, параллельная основанию треугольника, делит его на треугольник и трапецию, площади которых относятся как 4:5. Периметр образовавшегося треугольника равен 20 см. Найдите периметр данного треугольника.
3. Через вершину прямого угла прямоугольного треугольника с катетами 6 и 8 см проведен перпендикуляр к гипотенузе. Вычислите площади образовавшихся треугольников.
4. В трапеции ABCD меньшая диагональ BD, равная 6, перпендикулярна основаниям AD=3 и DC=12. Найдите сумму тупых углов B и D.
5. Основания трапеции равны a и b. Определите длину отрезка, параллельного основаниям и делящего трапецию на равновеликие части.
Задачи для изучения (с решением):
Пример №1: Покажите, что два треугольника на рисунке внизу являются подобными.
Решение:
Так как длины сторон обоих треугольников известны, то здесь можно применить третий признак подобия треугольников:
Т.к. все отношения равны 3, то треугольники подобны
Третий признак подобия треугольников
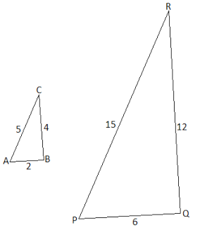
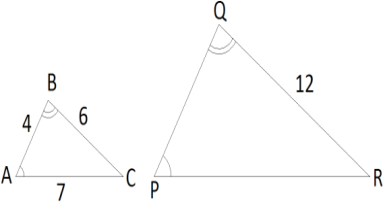
Пример №2: Докажите, что два данных треугольника являются подобными и определите длины сторон PQ и PR.
Первый признак подобия
Пример №3: Определите длину AB в данном треугольнике.
Первый признак подобия
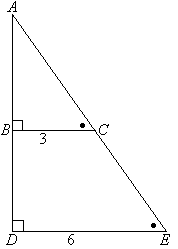
Пример №4:Определить длину AD (x) геометрической фигуры на рисунке.
Треугольники ΔABC и ΔCDE являются подобными так как AB || DE и у них общий верхний угол C.
Мы видим, что один треугольник является масштабированной версией другого. Однако нам нужно это доказать математически.
AB || DE, CD || AC и BC || EC
∠BAC = ∠EDC и ∠ABC = ∠DEC
Исходя из вышеизложенного и учитывая наличие общего угла C, мы можем утверждать, что треугольники ΔABC и ΔCDE подобны.
Следовательно:
x = AC — DC = 23,57 — 15 = 8,57
ТЕСТ
Видео:Решение задач на тему "Подобные треугольники". 8 классСкачать

Задачи с практическим содержанием по теме «Подобие треугольников»
Задачи с практическим содержанием по теме «Подобие треугольников»
Задача №1. Неприятельская вышка
Открытый участок дороги находится на полосе АВ шириной в 50м; неприятельский наблюдательный пункт находится на верху колокольни высотой MN = 22м. Какой высоты следует сделать вертикальную маску КВ на расстоянии 500м от колокольни, чтобы закрыть дорогу от наблюдателя противника?

MN = 22м,
BN = 500м








. Земля как на ладони, когда ты в небе на воздушном шаре
Как далеко видно с воздушного шара, поднявшегося на высоту 4 км над Землей (радиус Земли примерно равен 6370 км)?
1. По теореме о касательной к окружности, касательная перпендикулярна радиусу, проведенному в точку касания, то есть 
2. MO = 6370 + 4 = 6374 км,
3. тогда по теореме Пифагора:
MT 2 + OT 2 = MO 2
MT 2 = MO 2 – OT 2
MT = 112,9 км
На улице Притомская-Набережная стоит 17-тиэтажное здание, высота которого 500 м. Какой высоты следует вырастить дерево КВ, если человек стоит на 2 м. от него, чтобы закрыть дорогу и это здание от наблюдателя? (Расстояние между деревом и зданием 22 м ).

MN = 500м,
BN = 22м .Найти: КВ.





То есть, 


Что увидит человек, стоящий на крыше гостиницы Кристалл, если другой человек, рост которого 1,8 м, стоит на расстоянии 1,83 м от другого здания. Если можете, назовите это здание. (Здание гостиницы Кристалл 500 м.)
МКС (по 2-м углам)
Ответ: искомое здание ТРК «Лапландия».
Гора Эльбрус (на Кавказе) поднимается над уровнем моря на 5600м. Как далеко можно видеть с вершины этой горы?
М – наблюдательный пункт высотой h метров над Землей; радиус Земли R, MT = d есть наибольшее видимое расстояние. Доказать, что 
Вершина горы видна из точки А под углом 38 42’, а при приближении к горе на 200м вершина стала видна под углом 42. Найти высоту горы.
Задача из китайской «Математики в девяти книгах»
«Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды и какова длина камыша?».
Задача из учебника «Арифметика» Леонтия Магницкого.
«Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать».
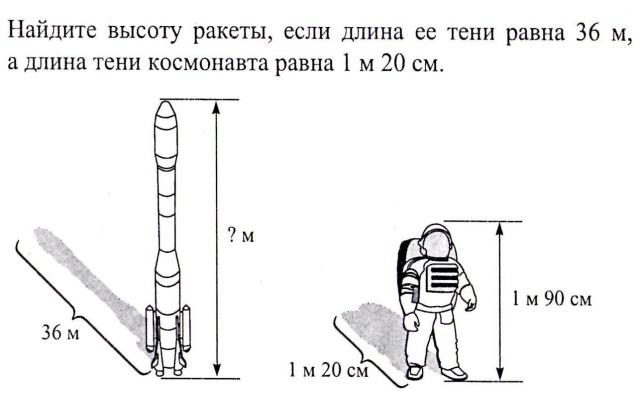
Измерение высоты дерева.
Для того, чтобы измерить высоту дерева BD, приготовили прямоугольный треугольник АВ1C1 с углом А = 45о и, держа его вертикально, отошли на такое расстояние, при котором, глядя вдоль гипотенузы АВ1, увидели верхушку дерева В. Какова высота дерева, если расстояние



АС = 5,6м
h человека = 1,7м.
1) Так как 




2) Тогда 

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Задачи наподобие треугольников повышенной сложности
Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 36. Решение задач на применение признаков подобия треугольников. Вернуться к Списку уроков Тематического планирования.
Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Урок 36. Решение задач на применение
признаков подобия треугольников
Основные дидактические цели урока: сформировать у учащихся навыки применения признаков подобия треугольников при решении задач; совершенствовать навыки доказательств теорем.
Ход урока
I. Организационный момент.
Мотивация к учебной деятельности. (Учитель сообщает тему урока, формулирует цели урока.)
II. Актуализация знаний учащихся
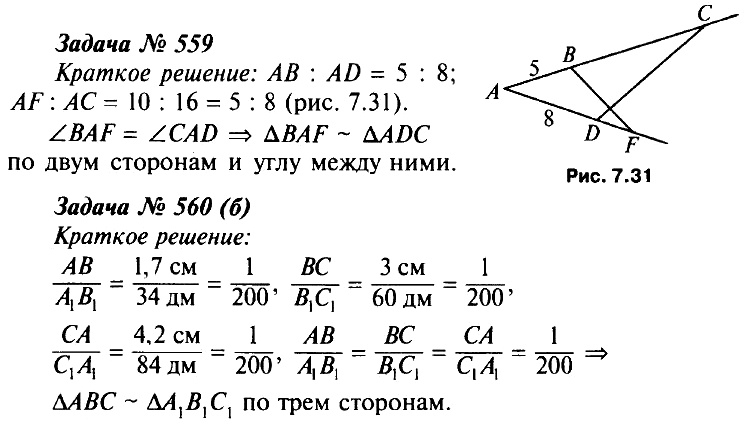
- Проверка домашнего задания. (Учитель проверяет решение задач № 559, 560 (б). Два ученика заранее готовят решение на доске.)
- Теоретический опрос. (Два ученика готовят доказательства теорем у доски.)
- Сформулируйте признаки подобия треугольников.
- Докажите теоремы, выражающие второй и третий признаки подобия треугольников.
- Работа по индивидуальным карточкам. (3—6 учеников работают по карточкам во время теоретического опроса.)
I уровень сложности
Подобны ли треугольники АВС и А1В1С1, если известно, что:
II уровень сложности
- Прямая, параллельная стороне MN треугольника MNK, пересекает стороны КМ и KN в точках Е и F соответственно, КЕ = 6 см, KN = 10 см, KF = 9 см, KN = 15 см. Найдите отношения. a) EF: MN, б) PKMN : РКЕF, в) SKEF : SKMN.
- Точка Е — середина стороны AD параллелограмма ABCD. В каком отношении прямая BE делит диагональ АС параллелограмма? Найдите отношение площади треугольника АВЕ и четырехугольника BCDE.
III уровень сложности
- Основания трапеции равны 9 и 6 см, а высота равна 10 см. Найдите разность расстояний от точки пересечения диагоналей трапеции до ее оснований.
- Докажите признак подобия прямоугольных треугольников по гипотенузе и катету.
- Решение задач по готовым чертежам.
- 1) Рис. 7.32. Найти: ∠C1, В1С1.
- 2) Рис. 7.33. Найти: ∠C, ∠C1
- 3) Рис. 7.34. Найти: ВМ.
- 4) Рис. 7.35. Найти: ВС.
- 5) Рис. 7.36. Найти: ∠DCA.
- 6) Рис. 7.37. Найти АВ, NC.
Ответы к задачам по готовым чертежам:
- 1) ∠C1 = 71°, В1С1 = 15 см.
- 2) ∠C = ∠C1 = 60°.
- 3) ВМ = 6 см.
- 4) BC = 20/3.
- 5)Обратите внимание! Ответ автора задания ∠DCA = 90°. Однако, этот ответ нельзя признать правильным в виду каких-то опечаток в рис.7.36. Единственный вывод из рисунка: треугольники ABC и АCD подобны (по трем сторонам), но в таком случае ответ должен быть 80°, а не 90°. Но самый противоречивый момент связан с тем, что треугольники с заявленными сторонами и углами не существуют. Если считать, что стороны на рисунке указаны правильно, то вместо 80° должно быть указано 92,73°, а вместо 55° должно быть 45,52°. Тогда правильный ответ будет ∠DCA = 92,73°.
- 6) АВ = 8, NC= 8.
(После окончания самостоятельного решения задач и самопроверки по готовым ответам выполняется самооценка.) Критерии оценивания:
- оценка «5» — правильно решены пять-шесть задачи;
- оценка «4» — правильно решены четыре задачи;
- оценка «3» — правильно решены две-три задачи;
- оценка «2» — не ставится.
(Учащиеся, справившиеся со всеми задачами, решают дополнительные задачи.)
Дополнительные задачи
- Диагональ АС трапеции ABCD (АВ||CD) делит ее на два подобных треугольника. Найдите площадь трапеции ABCD, если АВ = 25 см, ВС = 20 см, АС = 15 см.
Ответ : SABCD = 204 см 2 .
- Угол В треугольника AВС в два раза больше угла А. Биссектриса угла В делит сторону АС на части AD = 6 см и CD = 3 см. Найдите стороны треугольника АВС.
Ответ : АС = 9 см, АВ = 6√3 см, ВС = 3√3 см.
III. Самостоятельная работа
I уровень сложности
Вариант 1
- Рис. 7.38. Доказать: ΔАВС
ΔА1В1С1
Вариант 2
- Рис. 7.39. Доказать: ΔАВС
ΔА1B1С1.
II уровень сложности
Вариант 1.
- Рис. 7.40. Доказать: ΔАВС
ΔА1В1С1
Вариант 2
- Рис. 7.41. Доказать: ΔМВН
ΔСВA.
III уровень сложности
Вариант 1
- Дано: ∠1 = ∠2, AD = 4, АС = 9 (рис. 7.42). Найти: АВ, SABD : SABC.
- Диагонали четырехугольника ABCD пересекаются в точке О, АО • ВО = СО • DO. Докажите, что площади треугольников ACD и ABD равны.
Вариант 2
- Дано: ВС ⊥ АС, МН ⊥ ВС, 2МС = ВС, МН = 0,5АС (рис. 7.43). Доказать: АВ||СН. Найти. SАВС : SMCH.
- В трапеции ABCD AD и ВС — основания, О — точка пересечения диагоналей, АО : ОС = 3 : 2. Найдите отношение площадей треугольников АВС и ACD.
( Ответы на самостоятельную работу смотрите в уроке 37)
IV. Рефлексия учебной деятельности
- Сформулируйте признаки подобия треугольников.
- В каком случае подобны равносторонние, равнобедренные, прямоугольные треугольники?
Домашнее задание. Решить задачи № 562, 563, 604, 605.
Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 36. Решение задач на применение признаков подобия треугольников.
🌟 Видео
Сложная задача на подобие треугольников (видео 11)| Подобие. Геометрия | МатематикаСкачать

Задача на подобие треугольников 1частьСкачать

Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Первый признак подобия треугольников. Найти подобные по рисунку. Задачи на подобиеСкачать

Геометрия . Задачи на подобие треугольников. Изи.Скачать

Подобные треугольникиСкачать

Найти высоту дерева Задача на подобие треугольников 2 частьСкачать

Подобные треугольники с нуля до ОГЭ | Математика ОГЭ 2023 | УмскулСкачать

Задача на подобие треугольниковСкачать

Геометрия Задача повышенной трудности 7 класс учебник Атанасян №337/математика и фокусыСкачать

Задача, которой русские школьники мучали американскихСкачать

Задача 15 ОГЭ: подобные треугольники в трапецииСкачать

8 класс, 22 урок, Первый признак подобия треугольниковСкачать

Задача, которую боятсяСкачать

Задача повышенной сложности с подобием треугольниковСкачать