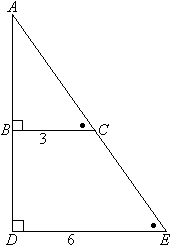Задачи наподобие треугольников из егэ

Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

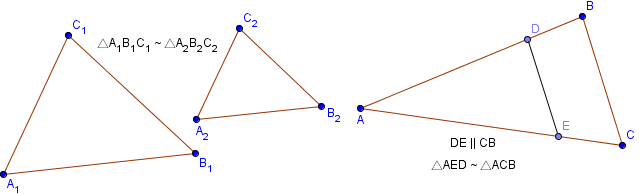
Определение

Как правило, два треугольника считаются подобными если они имеют одинаковую форму, даже если они различаются размерами, повернуты или даже перевернуты.

Математическое представление двух подобных треугольников A₁B₁C₁ и A₂B₂C₂ , показанных на рисунке, записывается следующим образом:

Два треугольника являются подобными если:

1. Каждый угол одного треугольника равен соответствующему углу другого треугольника:
∠A₁ = ∠A₂, ∠B₁ = ∠B₂ и∠C₁ = ∠C₂

2. Отношения сторон одного треугольника к соответствующим сторонам другого треугольника равны между собой:
$frac=frac=frac$

3. Отношения двух сторон одного треугольника к соответствующим сторонам другого треугольника равны между собой и при этом
углы между этими сторонами равны:
$frac=frac$ и $angle A_1 = angle A_2$
или
$frac=frac$ и $angle B_1 = angle B_2$
или
$frac=frac$ и $angle C_1 = angle C_2$

Не нужно путать подобные треугольники с равными треугольниками. У равных треугольников равны соответствующие длины сторон. Поэтому для равных треугольников:

Из этого следует что все равные треугольники являются подобными. Однако не все подобные треугольники являются равными.

Несмотря на то, что вышеприведенная запись показывает, что для выяснения, являются ли два треугольника подобными или нет, нам должны быть известны величины трех углов или длины трех сторон каждого треугольника, для решения задач с подобными треугольниками достаточно знать любые три величины из указанных выше для каждого треугольника. Эти величины могут составлять различные комбинации:

1) три угла каждого треугольника (длины сторон треугольников знать не нужно).

Или хотя бы 2 угла одного треугольника должны быть равны 2-м углам другого треугольника.
Так как если 2 угла равны, то третий угол также будет равным.(Величина третьего угла составляет 180 — угол1 — угол2)

2) длины сторон каждого треугольника (углы знать не нужно);

3) длины двух сторон и угол между ними.

Далее мы рассмотрим решение некоторых задач с подобными треугольниками. Сначала мы рассмотрим задачи, которые можно решить непосредственным использованием вышеуказанных правил, а затем обсудим некоторые практические задачи, которые решаются по методу подобных треугольников.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Практические задачи с подобными треугольниками

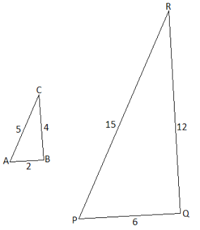
Пример №1: Покажите, что два треугольника на рисунке внизу являются подобными.

Решение:
Так как длины сторон обоих треугольников известны, то здесь можно применить второе правило:

Пример №2: Покажите, что два данных треугольника являются подобными и определите длины сторон PQ и PR.

Решение:
∠A = ∠P и ∠B = ∠Q, ∠C = ∠R(так как ∠C = 180 — ∠A — ∠B и ∠R = 180 — ∠P — ∠Q)

Из этого следует, что треугольники ΔABC и ΔPQR подобны. Следовательно:
$frac=frac=frac$

Пример №3: Определите длину AB в данном треугольнике.

Решение:

∠ABC = ∠ADE, ∠ACB = ∠AED и ∠A общий => треугольники ΔABC и ΔADE являются подобными.

$frac = frac = frac = frac = frac = frac Rightarrow 2times AB = AB + 4 Rightarrow AB = 4$

Пример №4:Определить длину AD (x) геометрической фигуры на рисунке.

Треугольники ΔABC и ΔCDE являются подобными так как AB || DE и у них общий верхний угол C.
Мы видим, что один треугольник является масштабированной версией другого. Однако нам нужно это доказать математически.

AB || DE, CD || AC и BC || EC
∠BAC = ∠EDC и ∠ABC = ∠DEC

Исходя из вышеизложенного и учитывая наличие общего угла C, мы можем утверждать, что треугольники ΔABC и ΔCDE подобны.

Следовательно:
$frac = frac = frac = frac Rightarrow CA = frac = 23.57$
x = AC — DC = 23.57 — 15 = 8.57

Практические примеры

Пример №5: На фабрике используется наклонная конвеерная лента для транспортировки продукции с уровня 1 на уровень 2, который выше уровня 1 на 3 метра, как показано на рисунке. Наклонный конвеер обслуживается с одного конца до уровня 1 и с другого конца до рабочего места, расположенного на расстоянии 8 метров от рабочей точки уровня 1.

Фабрика хочет модернизировать конвеер для доступа к новому уровню, который находится на расстоянии 9 метров над уровнем 1, и при этом сохранить угол наклона конвеера.

Определите расстояние, на котором нужно установить новый рабочий пункт для обеспечения работы конвеера на его новом конце на уровне 2. Также вычислите дополнительное расстояние, которое пройдет продукция при перемещении на новый уровень.

Решение:

Для начала давайте обозначим каждую точку пересечения определенной буквой, как показано на рисунке.

Исходя из рассуждений, приведенных выше в предыдущих примерах, мы можем сделать вывод о том, что треугольники ΔABC и ΔADE являются подобными. Следовательно,

$frac = frac = frac = frac Rightarrow AB = frac = 24 м$
x = AB — 8 = 24 — 8 = 16 м

Таким образом, новый пункт должен быть установлен на расстоянии 16 метров от уже существующего пункта.

А так как конструкция состоит из прямоугольных треугольников, мы можем вычислить расстояние перемещения продукции следующим образом:

Аналогично, $AC = sqrt = sqrt = 25.63 м$
что является расстоянием, которое проходит продукция в данный момент при попадании на существующий уровень.

y = AC — AE = 25.63 — 8.54 = 17.09 м
это дополнительное расстояние, которое должна пройти продукция для достижения нового уровня.

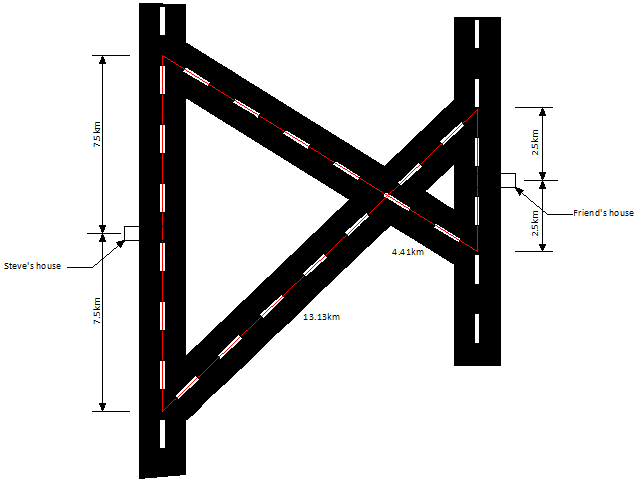
Пример №6: Стив хочет навестить своего приятеля, который недавно переехал в новый дом. Дорожная карта проезда к дому Стива и его приятеля вместе с известными Стиву расстояниями показана на рисунке. Помогите Стиву добраться к дому его приятеля наиболее коротким путем.

Решение:

Дорожную карту можно геометрически представить в следующем виде, как показано на рисунке.

Мы видим, что треугольники ΔABC и ΔCDE подобны, следовательно:
$frac = frac = frac$

В условии задачи сказано, что:

AB = 15 км, AC = 13.13 км, CD = 4.41 км и DE = 5 км

Используя эту информацию, мы можем вычислить следующие расстояния:

Стив может добраться к дому своего друга по следующим маршрутам:

A -> B -> C -> E -> G, суммарное расстояние равно 7.5+13.23+4.38+2.5=27.61 км

F -> B -> C -> D -> G, суммарное расстояние равно 7.5+13.23+4.41+2.5=27.64 км

F -> A -> C -> E -> G, суммарное расстояние равно 7.5+13.13+4.38+2.5=27.51 км

F -> A -> C -> D -> G, суммарное расстояние равно 7.5+13.13+4.41+2.5=27.54 км

Следовательно, маршрут №3 является наиболее коротким и может быть предложен Стиву.

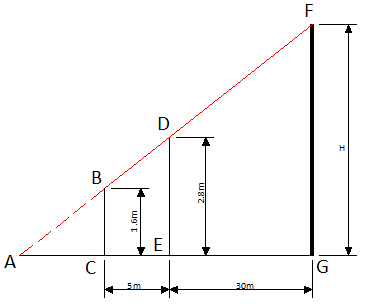
Пример 7:
Триша хочет измерить высоту дома, но у нее нет нужных инструментов. Она заметила, что перед домом растет дерево и решила применить свою находчивость и знания геометрии, полученные в школе, для определения высоты здания. Она измерила расстояние от дерева до дома, результат составил 30 м. Затем она встала перед деревом и начала отходить назад, пока верхний край здания стал виден над верхушкой дерева. Триша отметила это место и измерила расстояние от него до дерева. Это расстояние составило 5 м.

Высота дерева равна 2.8 м, а высота уровня глаз Триши равна 1.6 м. Помогите Трише определить высоту здания.

Решение:

Геометрическое представление задачи показано на рисунке.

Сначала мы используем подобность треугольников ΔABC и ΔADE.

$frac = frac = frac = frac Rightarrow 2.8 times AC = 1.6 times (5 + AC) = 8 + 1.6 times AC$

$(2.8 — 1.6) times AC = 8 Rightarrow AC = frac = 6.67$

Затем мы можем использовать подобность треугольников ΔACB и ΔAFG или ΔADE и ΔAFG. Давайте выберем первый вариант.

Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Готовимся к ОГЭ. Подобие треугольников. Задачи.
материал для подготовки к егэ (гиа) по геометрии (9 класс)

Задачи в формате ОГЭ по теме » Подобие треугольников».

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Скачать:

Видео:Задача на подобие треугольников 1частьСкачать

Предварительный просмотр:

№ 1. Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC . Найдите AB , если AH = 5, AC = 20.

№2 Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M . Найдите MC , если AB = 10, DC = 25, AC = 56 .

№3. Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M . Найдите MC , если AB = 16, DC = 24, AC = 25 .

№4. Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C . Найдите длину отрезка KP , если AP = 18, а сторона BC в 1,2 раза меньше стороны AB .

№5. Прямая, параллельная стороне AC треугольника ABC , пересекает стороны AB и BC в точках M и N соответственно. Найдите BN , если MN = 13, AC = 65, NC = 28.

№6. Высота треугольника разбивает его основание на два отрезка с длинами 8 и 9. Найдите длину этой высоты, если известно, что другая высота треугольника делит ее пополам.

№ 7. Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M . Найдите MC , если AB = 13, DC = 65, AC = 42.

№ 8. Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M . Найдите MC , если AB = 14, DC = 56, AC = 40 .

№9. Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C . Найдите длину отрезка KP , если AP = 7, а сторона BC в 1,4 раза меньше стороны AB .

Видео:Подобные треугольникиСкачать

По теме: методические разработки, презентации и конспекты

Учебное занятие по теме «Подобие треугольников. Решение практических задач»

В этом материале представлен подробный конспект урока по геометрии в 8 классе по теме «Подобие треугольников. Решение практических задач». Урок был составлен с учётом ФГОС.

Презентация по теме «Задачи на подобие треугольников»

презентация содержит задачи на отработку навыков решения задач по теме «Подобие треугольников».

Задачи на готовых чертежах по теме: «Признаки подобия треугольников» 8 класс

30 задач на готовых чертежах по теме «Признаки подобия треугольников&quot.

Готовимся к ОГЭ. Прямоугольный треугольник. Задачи.

Задачи в формате ОГЭ по теме «Прямоугольный треугольник&quot.

Подобие треугольников и применение подобия к решению задач

Конспект урока закрепления темы: Подобие треугольников. Решение задач подобие треугольников.

Решение задач по готовому чертежу ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ (1часть)

Дидактический материал для использования на уроке по теме «Решение задач на применение первого признака подобия треугольников&quot.

Решение задач по готовому чертежу ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ (2часть)

Дидактический материал для использования на уроке по теме «Решение задач на применение признаков подобия треугольников&quot.

Видео:Геометрия . Задачи на подобие треугольников. Изи.Скачать

Задачи на подобие треугольников в ЕГЭ

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Задачи на подобие треугольников в ЕГЭ.

Цель урока: повторить признаки подобия треугольников; детально рассмотреть задачу С4 ЕГЭ; ввести понятие ортотреугольника

Определение подобных треугольников Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия

Признаки подобия треугольников I признак подобия треугольников Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны

Признаки подобия треугольников II признак подобия треугольников Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны

Признаки подобия треугольников III признак подобия треугольников Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны

a c a b b d c d a c d b b d c d

Задача С4 Точки А1, В1, С1 – основания высот треугольника АВС. Углы треугольника А1В1С1 равны 90º, 60º и 30º. Найдите углы треугольника АВС.

Свойства ортотреугольника Ортотреугольник отсекает треугольники, подобные данному. Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника. 3. Высоты треугольника являются биссектрисами ортотреугольника. 4. Ортотреугольник – это треугольник с наименьшим периметром, который можно вписать в этот треугольник . 5. Периметр ортотреугольника равен удвоенному произведению высоты треугольника на синус угла, из которого она исходит. О

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 963 человека из 80 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 309 человек из 70 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 676 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Решение задач на тему "Подобные треугольники". 8 классСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 556 627 материалов в базе

Другие материалы

• 09.03.2018
• 356
• 1

• 09.03.2018
• 991
• 1

• 09.03.2018
• 51719
• 1336

• 09.03.2018
• 724
• 2

• 09.03.2018
• 4751
• 18

• 09.03.2018
• 2570
• 112

• 09.03.2018
• 455
• 4

• 09.03.2018
• 475
• 2

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 09.03.2018 1708
• PPTX 340 кбайт
• 15 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Ситдикова Ирина Масгутовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 3 месяца
• Подписчики: 0
• Всего просмотров: 17761
• Всего материалов: 10

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Найти высоту дерева Задача на подобие треугольников 2 частьСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

Новые курсы: управление детским садом, коучинг, немецкий язык и другие

Время чтения: 18 минут

Власти Бурятии заявили о нехватке школьных учителей и воспитателей

Время чтения: 2 минуты

В России могут объявить Десятилетие науки и технологий

Время чтения: 1 минута

Петербургская учительница уволилась после чтения на уроке Введенского и Хармса

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

💥 Видео

Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

ПОДОБНЫЕ ТРЕУГОЛЬНИКИ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

ЕГЭ задание 16 Шоу подобных треугольниковСкачать

Занятие 10. Подобие треугольников. Планиметрия для ЕГЭ и ОГЭСкачать

Вся геометрия треугольника в одной задаче. Планиметрия. ЕГЭ 2023 математика задача 16Скачать

ПОДОБИЕ НА ЕГЭ ПРОСТЫМ ЯЗЫКОМСкачать

ОГЭ геометрия задача на подобие треугольников про тень от фонаряСкачать

Сложная задача на подобие треугольников (видео 11)| Подобие. Геометрия | МатематикаСкачать

Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Коэффициент подобия отрезков/ площадей/ объемовСкачать

Задача из профильного ЕГЭСкачать