Дайте краткую характеристику новой математической модели тригонометрической окружности

Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Тригонометрия в прямоугольном треугольнике

Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.

sin α = Противолежащий катет гипотенуза

Косинус угла – отношение прилежащего катета к гипотенузе.

cos α = Прилежащий катет гипотенуза

Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).

tg α = Противолежащий катет Прилежащий катет

Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).

ctg α = Прилежащий катет Противолежащий катет

Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:

sin ∠ A = C B A B

cos ∠ A = A C A B

tg ∠ A = sin ∠ A cos ∠ A = C B A C

ctg ∠ A = cos ∠ A sin ∠ A = A C C B

sin ∠ B = A C A B

cos ∠ B = B C A B

tg ∠ B = sin ∠ B cos ∠ B = A C C B

ctg ∠ B = cos ∠ B sin ∠ B = C B A C

Видео:Тригонометрическая окружность. Как выучить?Скачать

Тригонометрия: Тригонометрический круг

Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.

Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.

Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )

На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.

Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .

Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .

Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .

Рассмотрим прямоугольный треугольник A O B :

cos α = O B O A = O B 1 = O B

sin α = A B O A = A B 1 = A B

Поскольку O C A B – прямоугольник, A B = C O .

Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).

Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :

Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .

Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .

Координата по оси x – косинус угла , координата по оси y – синус угла .

Ещё одно замечание.

Синус тупого угла – положительная величина, а косинус – отрицательная.

Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .

Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .

Видео:Математика это не ИсламСкачать

Основное тригонометрическое тождество

sin 2 α + cos 2 α = 1

Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :

A B 2 + O B 2 = O A 2

sin 2 α + cos 2 α = R 2

sin 2 α + cos 2 α = 1

Видео:Как искать точки на тригонометрической окружности.Скачать

Тригонометрия: Таблица значений тригонометрических функций

0 °30 °45 °60 °90 °sin α01 22 23 21cos α13 22 21 20tg α03 313нетctg αнет313 30

Видео:Тригонометрия. 10 класс. Вебинар | МатематикаСкачать

Тригонометрия: градусы и радианы

Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!

Видео:Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать

Тригонометрия: Формулы приведения

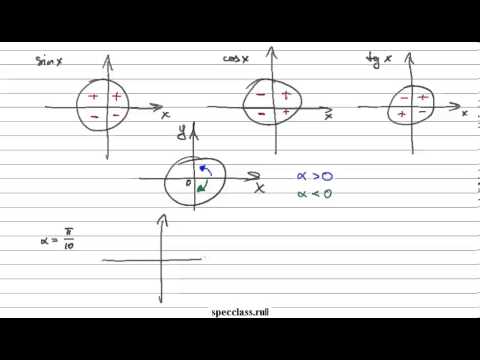
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:

sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °

sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °

sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °

sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °

cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °

cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °

cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °

cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °

Рассмотрим тупой угол β :

Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:

sin ( 180 ° − α ) = sin α

cos ( 180 ° − α ) = − cos α

tg ( 180 ° − α ) = − tg α

ctg ( 180 ° − α ) = − ctg α

Видео:Вся Тригонометрия для Чайников, 10 класс, урок 1Скачать

Тригонометрия: Теорема синусов

В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

a sin ∠ A = b sin ∠ B = c sin ∠ C

Видео:Найти знак тригонометрической функции (bezbotvy)Скачать

Тригонометрия: Расширенная теорема синусов

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R

Видео:Тригонометрическая окружностьСкачать

Тригонометрия: Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A

b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B

c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C

Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с тригонометрией.

Видео:Вся тригонометрия к ЕГЭ за 20 минут | Математика ЕГЭ — Эрик ЛегионСкачать

Тригонометрия: Тригонометрические уравнения

Это тема 10-11 классов.

Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!

Видео:Алгебра 10 класс. 15 сентября. Числовая окружность #1Скачать

творческий проект «Модель тригонометрической окружности»
проект по технологии на тему

творческая работа учащихся по улучшению материально-технической базы школы

Видео:ФОРМУЛЫ ПРИВЕДЕНИЯ (Тригонометрия ЕГЭ 2024 Математика Профиль)Скачать

Скачать:

Видео:Тригонометрическая окружность. Задание 4 | Математика ЕГЭ 2022 | УмскулСкачать

Предварительный просмотр:

МБОУ «СОШ п. Муслюмово ж.д. станции»

«Модель тригонометрической окружности»

Подготовили: Галимов М. Филатов В.

Проверил: Галимов А.З.

п. Муслюмово ж.д. станции.

Обоснование возникшей проблемы и потребности

Данный проект выполнен по просьбе учителя математики для успешного изучения учащимися тригонометрических функций. Не секрет, что подобные модели способствуют лучшему пониманию учебного материала. Но купить подобные изделия довольно затруднительно. Чтобы достигнуть этого, вовсе нет необходимости затрачивать большие средства. Для этого необходимо многое сделать своими руками.

Главное в этом проекте то, что изделие можно сделать самостоятельно. При выборе данного проекта были учтены следующие моменты.

В процессе изготовления этого изделия используются приобретенные знания, умения и навыки в области математики, физики, химии и технологии. Изготовление этого изделия способствует закреплению ранее изученного материала таких тем, как «Разметка», «Пиление», «Сверление», «Ремонт мебели в быту».

Оснащение учебных мастерских позволяет выполнить этот проект, данная работа не опасна. В процессе выполнения можно ознакомиться с технологией выполнения операций электролобзиком, приобрести практические навыки по изготовлению изделий..

Изготовив такой макет, можно внести личный вклад в оформление кабинета, сделав приятный подарок своим учителям.

При изготовлении макета требуется соблюдать точность и аккуратность.

Внешний вид изделия

5 х 30

Болт с 2-мя гайками

Разметить по размеру и выпилить из заготовки – листа многослойной фанеры деталь основания

Линейка, столяр-ный угольник, ножовка

Зачистить и отделать кромки детали основания

Напильник, наж-дачная бумага.

Выполнить разметку окружности. В центре окружности просверлить отверстие диаметром 6 мм.

Циркуль, сверло, шило, электродрель

Разметить по размеру и выпилить из заготовки – листа многослойной фанеры деталь длинной стрелки

Линейка, столяр-ный угольник, электролобзик

Зачистить и отделать кромки детали длинной стрелки

Напильник, наж-дачная бумага.

Разметить по размеру и выпилить из заготовки – листа многослойной фанеры деталь короткой стрелки

Линейка, столяр-ный угольник, электролобзик

Зачистить и отделать кромки детали короткой стрелки,

Напильник, наж-дачная бумага.

Разметить и просверлить на длинной стрелке 2 отверстия диаметром 6 мм.

Сверло, шило, электродрель

Разметить и просверлить на короткой стрелке 1 отверстие диаметром 6 мм.

Сверло, шило, электродрель

С помощью заклепки-оси свободно закрепить на длинной стрелке короткую стрелку

При помощи болта и 2 гаек закрепить длинную стрелку к основанию

Выполнить необходимую зачистку, покрыть олифой, после высыхания покрыть лаком.

Наждачная шкурка, кисть.

1. Расчет стоимости древесных материалов:

Для изготовления модели тригонометрической окружности понадобилось фанеры:

1/ Основание: Sосн. = 70см. х 70см. = 4900 кв.см. = 0,49 кв.м.

2/ Стрелка длинная: Sдл.стр. = 45см. х 5см. = 225 кв.см. = 0,0225 кв.м.

3/ Стрелка короткая:Sкор.стр. = 34см. х 5см. = 170 кв.см. = 0,017 кв.м.

Итого израсходовано фанеры: Sф = 0,49кв.м. + 0,0225 кв.м. + 0,017 кв.м. = 0,5295 кв.м.

Находим стоимость израсходованных древесных материалов (фанеры): Условная цена одного листа фанеры площадью 4,6 кв.м. – 1200 рублей. Стоимость израсходованной фанеры: Сф. = (1200 х 0,5295)/4,6 = 138 рублей.

1. Расчет стоимости электроэнергии:

Для выполнения распиловочных и сверлильных работ были использованы электролобзик и электродрель мощностью 0,3 квт. Для выполнения работ понадобилось 0,5 часа. Находим стоимость израсходованной электроэнергии. Цена 1 квт.ч. = 2,04 рубля. Таким образом стоимость израсходованной электроэнергии:

Сэл. = 0,3 х 0,5 х 2,04 = 0,3 рубля.

1. Расчет стоимости крепежных материалов:

Болты и гайки были куплены в магазине. Скр.мат. = 12 рублей.

Таким образом общая стоимость изделия составляет:

Сизд. = Сф. + Сэл. + Скр.мат. = 138 + 0,3 + 12 = 150,3 рубля.

Правила безопасности во время работы.

При выполнении операций ручной обработки древесины необходимо:

1.Правильно надеть спецодежду, проверить наличие инвентаря, разложить на верстаке инструменты. На верстаке не должно быть ничего лишнего. 2. Надежно закреплять обрабатываемый материал. 3. Пользоваться инструментом только по назначению, инструмент должен быть исправным, хорошо настроенным и заточенным. 4. Технологические операции (пиление, строгание, долбление, соединение деталей) выполнять на верстаке в установленных местах, использовать приспособления, упоры и подкладные доски. 5. Не допускать захламленности верстака отходами, стружками. Своевременно возвращать инструменты общего пользования. 6. Не отвлекаться во время работы, следить за правильными приемами работы. 7. После окончания работы остатки материалов, незаконченные детали изделия сдать дежурному или учителю, положить на место инструменты и приспособления, убрать свое рабочее место. Запрещается сдувать стружку ртом или сметать рукой.

Контроль качества, экологическое обоснование и самооценка.

Готовое изделие отвечает следующим требованиям:

Изделие изготовлено из древесного материала – многослойной фанеры. Все детали изготовлены аккуратно в соответствии с вышеуказанной технологией. Изделие представляет собой законченную конструкцию. Внешний вид изделия производит благоприятное впечатление.

Изделия из многослойной фанеры широко применяются в мебельном производстве. Так как они покрываются олифой, а затем мебельным лаком – они экологически безопасны. Изделие изготовлено собственными силами, удобно в использовании, обошлось намного дешевле.

Видео:Вариант #20 из задач ФИПИ - Уровень Сложности ЕГЭ 2024| Математика Профиль| Оформление на 100 БалловСкачать

По теме: методические разработки, презентации и конспекты

Обобщение метода интервалов на тригонометрической окружности

В данной работе описан метод решения тригонометрических неравенств с помощью числовой окружности. Материал может быть использован при разработке факультативных занятий по алгебре в 10 класс.

Открытый урок по теме «Решение тригонометрических уравнений с помощью единичной окружности»

Тригонометрическая окружность.

Интерактивная презентация в котоорой рассматривается единичная окружность, соответствие между точкой единичной окружности и углом поворота.Новые знания закрепляются в игровой форме.

Зачет №1 по алгебре и начала анализа 10 класса по теме «Числовая окружность, тригонометрические функции»

Материал зачетной работы предназначен для учащихся 10 класса заочной формы обучения и самообразования.

Окружной смотр- конкурс художественно- изобразительного, декоративно-прикладных и технических видов творческих проектов «Огонь друг,огонь враг»

Работы выполнены в технике «коллаж». Декоративная отделка древесины.

Тригонометрический диктант 10 класс. Координаты точек на единичной окружности

Тригонометрический диктант 10 класс. Координаты точек на единичной окружности. Презентация и раздаточный материал для обучающихся.

Видео:Формулы тригонометрии | Профильная математика ЕГЭ 2023 | УмскулСкачать

Тригонометрический круг: вся тригонометрия на одном рисунке

Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.

Вот что мы видим на этом рисунке:

Видео:Профильный ЕГЭ 2024. Задача 6. Формулы тригонометрии. 10 классСкачать

А теперь подробно о тригонометрическом круге:

Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.

Мы отсчитываем углы от положительного направления оси против часовой стрелки.

Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Всё это легко увидеть на нашем рисунке.

Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :

Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).

Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.

Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.

Легко заметить, что

Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:

где — целое число. То же самое можно записать в радианах:

Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,

🎬 Видео

Тригонометрические функции, y=tgx и y=ctgx, их свойства и графики. 10 класс.Скачать

СУТЬ ТРИГОНОМЕТРИИСкачать

Формулы приведения с нуля за 15 минут!Скачать