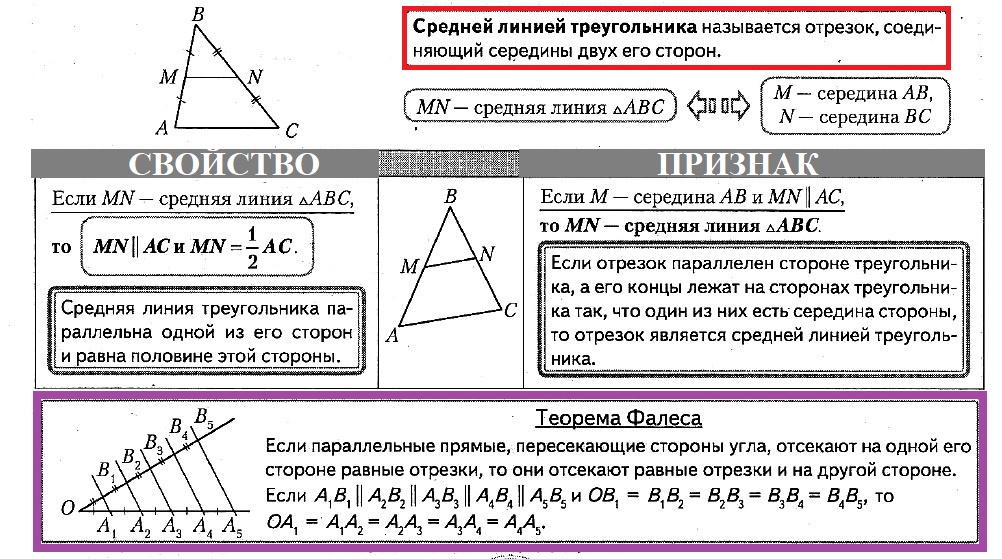
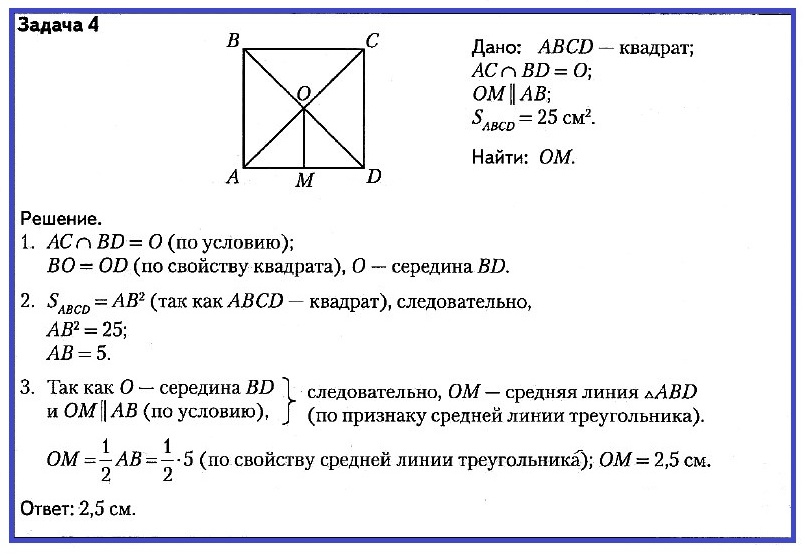
Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
Свойства средней линии треугольника:
1. Средняя линия параллельна третьей стороне и равна ее половине.
2. Средняя линия трeугольника отсекает от него треугольник, подобный данному (с коэффициентом подобия 1/2 ).
3. Три средние линии треугольника делят его на 4 равных треугольника, подобных данному, с коэффициентом подобия 1/2.
Свойство средней линии треугольника является следствием теоремы Фалеса.
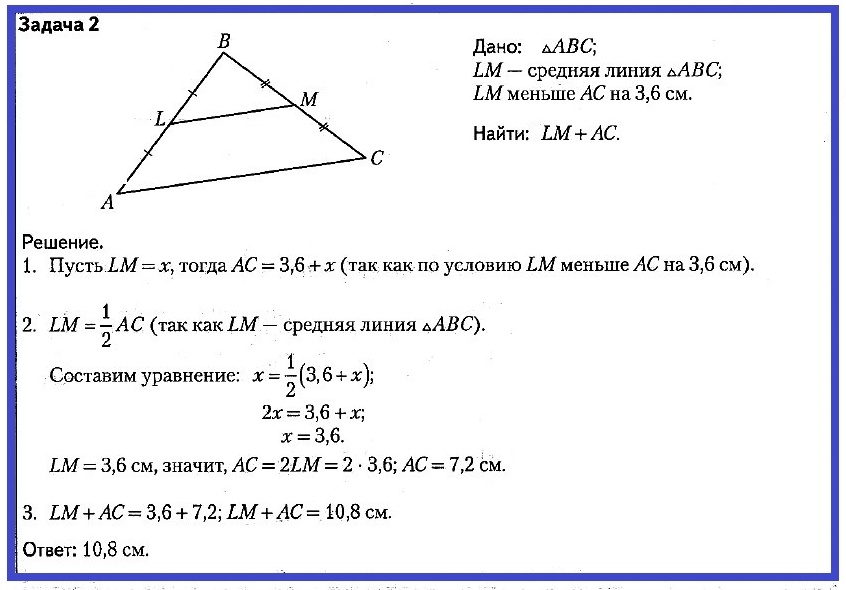
ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ
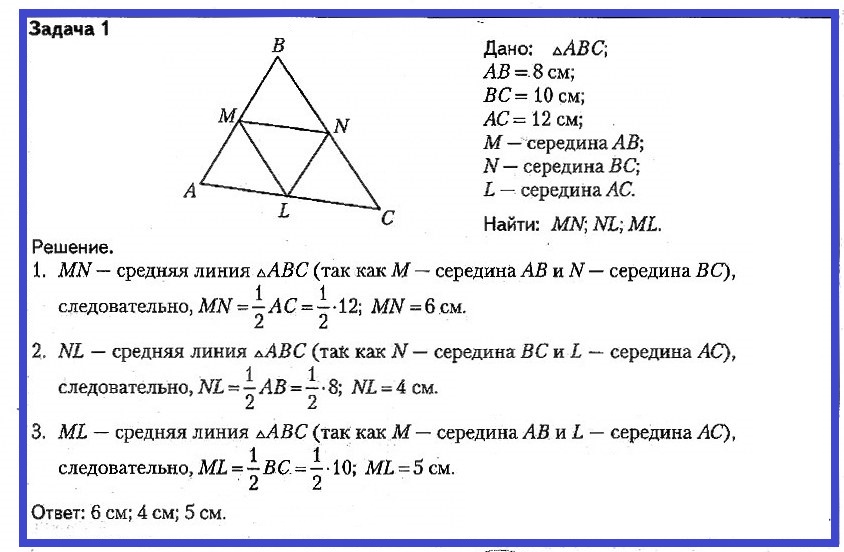
Задача № 1. Дано: ΔABC; AB = 8 см; BC = 10 см; AC = 12 см; M — середина AB; N — середина BC; L — середина AC. Найти: MN, NL, ML.
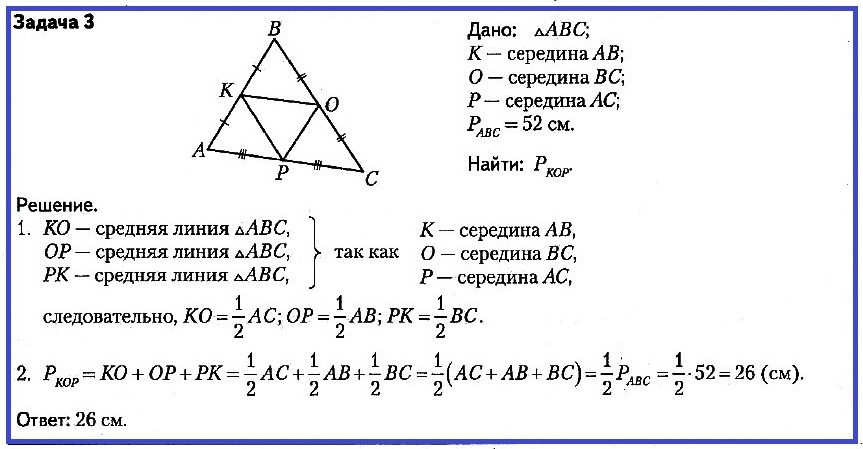
Задача № 3. ΔABC; K — середина AB; O — середина BC; P — середина AC; PABC = 52 см. Найти: PКOР
Это конспект по теме «Средняя линия треугольника + Задачи по теме». Выберите дальнейшие действия:
Видео:8 класс, 25 урок, Средняя линия треугольникаСкачать

Задачи по теме:»Средняя линия треугольника» 8 класс
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
1.Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 20, сторона BC равна 58, сторона AC равна 64. Найдите MN.
2. В треугольнике ABC точки M, N, K – середины сторон AB, BC, AC. Найти периметр треугольника ABC, если MN=12, MK=10, KN=8.
3.В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
4.Периметр равностороннего треугольника АВС равен 24 см. Найдите длину средней линии этого треугольника.
5.Стороны треугольника равны 2 см, 3 см и 4 см. Его вершины являются серединами сторон второго треугольника. Найдите периметр второго треугольника.
6.Периметр треугольника равен 12 см, середины сторон соединены отрезками. Найдите периметр получившегося треугольника.
7.Периметр равностороннего треугольника равен 72 см. Найдите его среднюю линию.
8.Периметр треугольника равен 12 см. Найдите периметр треугольника, отсекаемого от данного какой-нибудь его средней линией.
9.Средняя линия равнобедренного треугольника, параллельная основанию, равна 3 см. Найдите стороны треугольника, если его периметр равен 16 см.
10.Через вершины треугольника проведены прямые, параллельные его противоположным сторонам. Найдите периметр треугольника, ограниченного этими прямыми, если периметр исходного треугольника равен 6 см.
11.В треугольнике ABC DE — средняя линия. Площадь треугольника CDE равна 9. Найдите площадь треугольника ABC.
12.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 45. Найдите площадь треугольника ABC.
13.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 94. Найдите площадь треугольника ABC.
14.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 7. Найдите площадь треугольника ABC.
15.В треугольнике ABC отрезок DE — средняя линия. Площадь треугольника CDE равна 97. Найдите площадь треугольника ABC.
16.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 24. Найдите площадь треугольника ABC.
17.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 97. Найдите площадь треугольника ABC.
18.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 21. Найдите площадь треугольника ABC.
19.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 89. Найдите площадь треугольника ABC.
20.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 8. Найдите площадь треугольника ABC.
21.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 96. Найдите площадь треугольника ABC.
22.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 57. Найдите площадь треугольника ABC.
23.На клетчатой бумаге с размером клетки 1х1 изображён треугольник . Найдите длину его средней линии, параллельной стороне .
Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Что такое средняя линия треугольника
В данной публикации мы рассмотрим определение, свойства и признак средней линии треугольника, а также разберем пример решения задачи для лучшего понимания теоретического материала.
Видео:Геометрия 8. Средняя линия трапеции. Средняя линия треугольника. Задачи.Скачать

Определение средней линии треугольника
Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией.
- KL – средняя линия треугольника ABC
- K – середина стороны AB: AK = KB
- L – середина стороны BC: BL = LC
Видео:Средняя линия треугольника. Задачи по готовым чертежамСкачать

Свойства средней линии треугольника
Свойство 1
Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и в два раза меньше этой стороны.
На рисунке выше:
Свойство 2
Средняя линия треугольника отсекает от него подобный треугольник (в соотношении 1:2), площадь которого в 4 раза меньше исходного.
На рисунке выше:
- △KBL ∼ △ABC (подобие по пропорциональности всех сторон)
- Стороны △KBL в два раза меньше соответствующих сторон △ABC:
AB = 2KB, BC = 2BL, AC = 2KL. - S△ABC = 4 ⋅ S△KBL
Свойство 3
В любом треугольнике можно провести три средние линии.
KL, KM и ML – средние линии треугольника ABC.
Свойство 4
Три средние линии треугольника делят его на 4 равных по площади треугольника.
Видео:СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА 8 класс Атанасян геометрияСкачать

Признак средней линии треугольника
Отрезок, проходящий через середину одной из сторон треугольника, пресекающий вторую и параллельный третьей стороне, является средней линией этого треугольника.
Видео:Средняя линия. Теорема о средней линии треугольникаСкачать

Пример задачи
Дан треугольник, две стороны которого равны 6 и 8 см. Найдите длину средней линии, соединяющей эти стороны.
Треугольник с заданными сторонами является прямоугольным, причем известные значения – это длины катетов. Средняя линия, которая соединяет катеты, параллельна гипотенузе и равна половине ее длины.
Мы можем найти гипотенузу, воспользовавшись теоремой Пифагора.
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
BC = 10.
Таким образом, средняя линия LM = 1 /2 ⋅ BC = 1 /2 ⋅ 10 = 5.
💥 Видео
Геометрия 8. Урок 7 - Средняя линия треугольника и трапецииСкачать

Средняя линия треугольникаСкачать
Геометрия 7. Урок 8 - Признаки равенства треугольников.Скачать

Теорема Фалеса. Практическая часть - решение задачи. 8 класс.Скачать

64. Средняя линия треугольникаСкачать

Средняя линия треугольника. Видеоурок 13. Геометрия 8 класс.Скачать

Средняя линия треугольника – 8 класс геометрияСкачать

Теорема о средней линии треугольникаСкачать

Этой задачей русские дети 10 лет мучили американцев. Американцы не понимали, что делают не такСкачать

МАТЕМАТИКА | Средняя линия треугольникаСкачать

СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА . §7 геометрия 8 классСкачать

Теорема о средней линии треугольника. Доказательство. 8 класс.Скачать

В треугольнике ABC DE – средняя линия ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ #математика #егэ #shorts #профильныйегэСкачать