История возникновения биссектрисы треугольника

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

«Несколько интересных фактов о биссектрисе».

«Крупное научное открытие даёт решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия.» Д. Пойя

Биссектриса это интересная и удивительная фигура. Кроме того, в школьном курсе геометрии мы имеем также дело с таким понятием как треугольник. И к числу основных геометрических фактов следует отнести теорему о том, что биссектриса делит противоположную сторону треугольника в отношении прилежащих сторон. Этот факт остался в тени у более известных теорем и в первую очередь потому, что в большинстве учебников он находится в ряду задач. Но повсеместно встречаются задачи, которые гораздо легче решить, если знать этот и некоторые другие факты о биссектрисе. Так, например, ещё Архимед пользовался теоремой о биссектрисе, которая делит основание на части, пропорциональные боковым сторонам для того, чтобы определить длины полустороны 12-угольника , 24-угольника и т. д. Я заинтересовалась этим объектом и решила более подробно его изучить. Некоторый материал был найден в дополнительной литературе, но ответа на все свои вопросы, касающиеся этой темы, найдено не было. В связи с этим я провела самостоятельное исследование. Данная теорема интересна тем, что ее доказательств существует много. Я решила в своей работе показать некоторые варианты доказательства этой теоремы. И отметить некоторые другие интересные свойства биссектрисы.

Гипотеза: Что можно найти интересного о биссектрисе за страницами школьного учебника?

Цели: Получение новой информации о биссектрисе.

Изучить дополнительную литературу по данной теме.

Найти как можно больше доказательств теоремы о биссектрисе угла треугольника.

Показать значение теоремы в развитие математики.

Разнообразить материал различными дополнительными сведениями.

Сделать выводы и дать рекомендации по использованию данного материала.

Предмет исследования: биссектриса.

Объектом исследования является:

свойства биссектрисы треугольника;

Методы работы: работа с литературой, анализ, сравнение, обобщение полученной информации.

Краткая характеристика источников: Для проведения данного исследования использована энциклопедическая и учебная литература разных годов издания и разных авторов, Internet ресурсы.

Применение: Использовать наши знания и умения на уроках, на занятиях кружка, в методике преподавания геометрии в школе, при решении задач ЕГЭ.

Этапы работы: 1. Сбор информации и изучение литературы.

2.Рассмотрение различных доказательств теоремы о биссектрисе треугольника и некоторых свойств биссектрисы треугольника.

3. Поиск занимательной информации о биссектрисе.

4. Обработка результатов.

Биссектриса треугольника и некоторые её свойства:

а) Определение биссектрисы, биссектрисы треугольника.

б) Основное свойство биссектрисы треугольника – и его 17 доказательств;

в) Точка пересечения биссектрис треугольника;

г) Ещё одно свойство равнобедренного треугольника или теорема Штейнера — Лемуса;

Вычисления длины биссектрисы;

Занимательная информация о биссектрисе.

Заключение и вывод.

Биссектриса треугольника и некоторые её свойства:

а) Определение биссектрисы, биссектриса треугольника

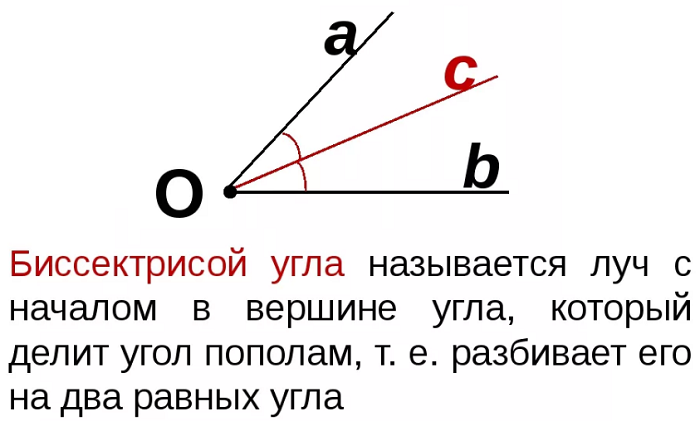
Определение биссектрисы угла:

Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.

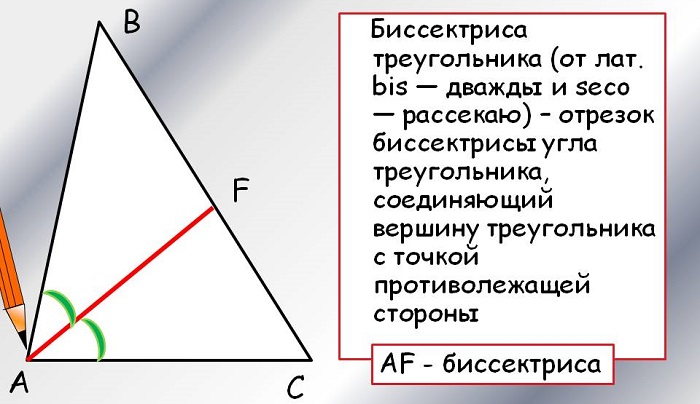
Определение биссектрисы треугольника:

Биссектрисой угла треугольника называется наибольший отрезок биссектрисы угла, лежащий внутри треугольника.

б) Основное свойство биссектрисы треугольника – и его 17 доказательств

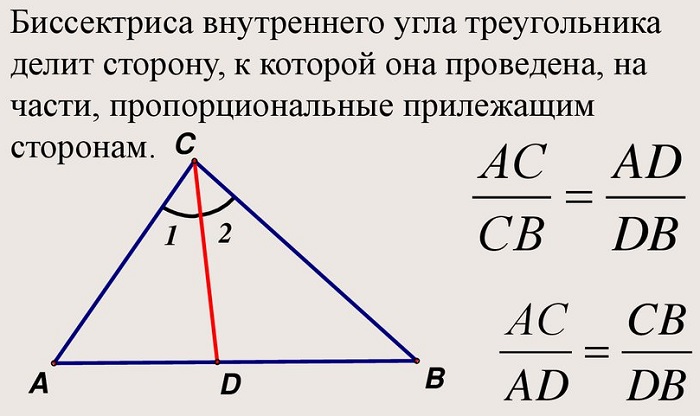
Теорема о биссектрисе треугольника:

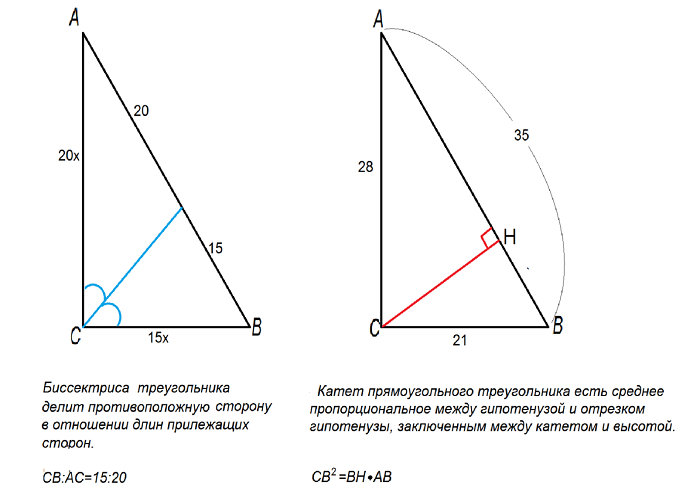
Основание биссектрисы внутреннего угла треугольника делит его сторону на части, пропорциональные прилежащим сторонам, т.е. согласно имеющемуся рисунку .

Удобно теорему формулировать так:

а) существует t такое, что и ;

б) существует k такое, что и .

17 доказательств теоремы о биссектрисе треугольника.

Теорема. Биссектриса BD внутреннего угла треугольника ABC делит противоположную сторону на отрезки, пропорциональные сторонам BC и ВА треугольника.

Первое доказательство теоремы о биссектрисе к рис №1.

Проведем через точку С прямую m , параллельную BD .

Тогда m AB = D ₁ и ∆ ABD ∆ AD ₁ C ; так как ABD = CBD = BCD ₁ = CD ₁ B , получаем BC = BD ₁ и AD ₁ : AB = AC : AD отсюда последовательно получаем

(AB + BC) : AB =(AD + DC): AD, => 1 + BC : AB = 1 + DC : AD.

Откуда следует, что BC : AB = DC : AD , что и требовалось доказать.

Второе доказательство к рис №1.

S _CBD : S _ABD = (0,5 · CB · DB · sinB /2) : (0,5 · AB · DB · sinB /2) = (0,5 · CD · h ) : (0,5 · AD · h ),

где h – длина высоты треугольника ABC , проведенной из вершины B .Отсюда

BC : AB = DC : AD , что и требовалось доказать.

Третье доказательство к рис №1.

По теореме синусов:

sin B/2 : CD = sin C : BD, sin B/2 : AD = sin A : BD, или sin B/2 : (CD · sin C ) = 1: BD и

sin B/2 : (AD · sin A) = 1: BD. Откуда sin B /2 : ( CD · sin C ) = sin B /2 : ( AD · sin A ), или CD : AD = CB : AB , что и требовалось доказать .

Четвертое доказательство к рис №2.

По теореме синусов:

Пусть . По теореме синусов в треугольнике ABL а в треугольнике ACL . Так как то, поделив обе части одного равенства на соответствующие части другого, поучим , что и требовалось доказать.

Пятое доказательство к рис №2.

Применим метод площадей. Вычислим площади треугольников ABL и ACL двумя способами:

Отсюда , что и требовалось доказать.

Шестое доказательство к рис №3.

Площади треугольников, имеющих равные высоты, относятся как соответствующие им основания. Поэтому S _BDA : S _BDC = AD : DC . С другой стороны, по свойству биссектрисы, высоты в треугольниках BDA и BDC , опущенные из вершины D , равны. Следовательно,

S _BDA : S _BDC = AB : CB . Итак, AD : CD = AB : CB = S _BDA : S _BDC . Итак AD : CD = AB : CB , что и требовалось доказать.

Выполнив осевую симметрию S треугольника ABC относительно BD (рис. 4), получим S _BD ( A ) = A ₁, S _BD ( C ) = C ₁ и S _BD = B .

Тогда ∆ CDC ₁ ∆ ADA ₁ и ∆ CC ₁ B ∆ AA ₁ B . Отсюда (учитывая, что AB = A ₁ B ),

CD : AD = CC ₁ : AA ₁ , CC ₁ : AA ₁ = CB : AB. Следовательно CD : AD = CB : AB , что и требовалось доказать.

Построим на луче BD точку Е, такую, что АЕ = AD .( Рис №5 а). Тогда АЕВ = ADE = BDC . Следовательно, треугольники А B Е и CBD подобны (по двум углам). Это значит, что

AE : С D = A В : BC . Приняв во внимание, АЕ = AD , получим AD : CD = AB : CB , что и требовалось доказать.

Построим на луче BD точку Е, такую, что AE = AB . (Рис № 5 б). Тогда AED = ABD , то есть треугольники AED и CBD подобны. Из подобия имеем AD : CD = AE : CB . Поскольку АЕ = AB , то AD : CD = AB : CB и теорема доказана.

Из вершин А и С опустим перпендикуляры АЕ и CF на прямую BD . (рис №6) Из подобия прямоугольных треугольников ADE и CDF получим AD : CD = AE : CF . В то же время из подобия прямоугольных треугольников ABE и CBF будем иметь AB : CB = AE : CF . В полученных пропорциях правые отношения равны, поэтому равны и левые, то есть AD : CD = AB : CB , что и требовалось доказать.

Проведем через точку D прямую, параллельную стороне АВ. (рис №7) Тогда по обобщенной теореме Фалеса AD : CD = BF : FC . Из подобия треугольников ACB и DCF имеем

AB : BC = FD : FC , и так как ∆ BFD – равнобедренный ( BDF = ABD , как накрест лежащие при параллельных прямых DF и AB и секущей BD , а ABD = DBF , отсюда BDF = DBF ) и BF = FD , то AB : CB = BF : FC . Следовательно, AD : CD = AB : CB (оба отношения равны

BF : FC ) что и требовалось доказать.

Опишем вокруг треугольника ABC окружность и продолжим BD до пересечения с окружностью в точке Е. (рис № 8) Из подобия треугольников ABE и DBC получаем AB : AE = BD : DC , то есть AB ∙ DC = AE ∙ BD . Из подобия треугольников CBE и DBA имеем CB : CE = BD : AD , то есть CB ∙ AD = CE ∙ BD . Заметив, что АЕ = СЕ, получим AB ∙ DC = CB ∙ AD , откуда AD : CD = AB : CB , что и требовалось доказать.

Проведем через точку D две прямые, одна из которых параллельна стороне АВ и пересекает сторону ВС в точке М, а другая – параллельна стороне ВС и пересекает сторону АВ в точке К(рис. 9) . Легко доказать, что четырехугольник КВМ D – ромб. Из подобия треугольников АК D и D МС имеем AD : С D = DK : С M . Так как DK = DM , то AD : CD = DM : CM . Заменив в полученной пропорции отношение DM : CM равным ему отношением АВ : СВ (на основании подобия треугольников ABC и DMC ), получим AD : CD = AB : CB , что и требовалось доказать.

Дано AL – биссектриса треугольника ABC . Требуется доказать, что

Пусть F – точка пересечения прямой AL и прямой, проходящей через точку B параллельно стороне AC . Тогда BFA = FAC = BAF . Следовательно, треугольник BAF равнобедренный и BA = BF . Из подобия треугольников ALC и FLB имеем соотношение откуда Что и требовалось доказать.

Пусть F – точка пересечения прямой AL и прямой, проходящей через точку C параллельно стороне AB (рис №11) Тогда можно повторить рассуждения. Теорема доказана.

Пусть К и М – основания перпендикуляров, опущенных на прямую AL из точек B и C соответственно (рис №12). Треугольники AB К и AC М подобны по двум углам. Поэтому . Из подобия треугольников B К L и C М L имеем . Отсюда . Теорема доказана.

А

Пусть А D – биссектриса треугольника ABC . Докажем, что BD : AB = CD : AC (рис №13). Треугольники ABD и ACD имеют общую высоту AH , поэтому S _ABD : S _ACD = BD : CD . С другой стороны, эти же треугольники имеют по равному углу ( 1 = 2), поэтому S _ABD : S _ACD = ( AB · AD ) : ( AC · AD ) = AB : AC . Из двух равенств для отношения площадей получаем

BD : CD = AB : AC , или BD : AB = CD : AC , что и требовалось доказать.

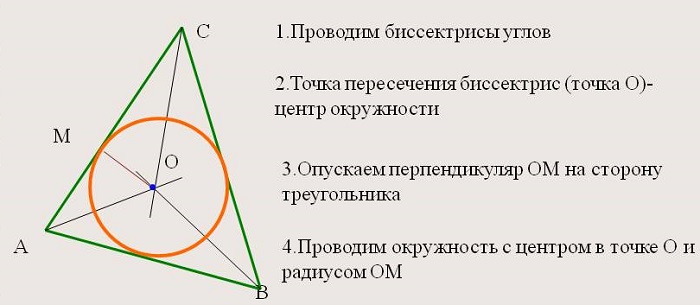
в) Точка пересечения биссектрис треугольника

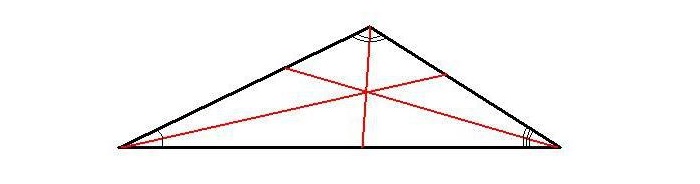
Теорема: Все три биссектрисы треугольника пересекаются в одной точке.

Пусть О – точка пересечения биссектрис АА ₁ и ВВ ₁ ; D , E и F – основания перпендикуляров, опущенныхиз точки P на АВ, В C и А C соответственно. (см рис №14) Треугольник AOE и AOF равны по гипотенузе и острому углу, отсюда OE = OF .

Аналогично, из равенства треугольников BOF и BOD , получим OF = OD . Следовательно, O E = OD , а значит, равны по гипотенузе и катету и треугольники OCD и OCE .Откуда следует, что OCD = OCE , т.е. CO – биссектриса угла DCE , а это означает, что третья биссектриса проходит через точку пересечения двух первых.

Замечание. Из приведенного доказательства следует, что точка пересечения биссектрис одинаково удалена от всех трех сторон треугольника, т. Е. является центром вписанной окружности. Окружность касающаяся стороны треугольника и продолжений двух других сторон называется вневписанной. Точно такими же рассуждениями можно доказать, что точка пересечения биссектрисы внутреннего угла треугольника и биссектрис двух внешних углов – центр вписанной окружности.

Теорема: Каждая биссектриса делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.

Доказательство:

Пусть О – точка пересечения биссектрис. (см рис. №15) AB = c, BC = a, AC = b. Тогда . Откуда Так как АО – биссектриса внутреннего угла треугольника BAC _, то АО : ОА₁ = АВ ₁ : В₁С + АС₁ : С₁В по теореме Ван – Обеля. Отсюда получаем

АО : ОА₁ = (с + в) : а, что и требовалось доказать.

Теорема: Если О – точка пересечения биссектрис треугольника АВС и АВС = β, тогда

Доказательство: Пусть А = α, В = β, С = γ. (см рис. №16) По теореме о сумме углов треугольника имеем α + β + γ = 180 . АОС = 180 — 0,5α — 0,5 γ = 180 — 0,5 (180 — β) = 90 + 0,5β = 90 + β/2, что и требовалось доказать.

г) Ещё одно свойство равнобедренного треугольника или теорема Штейнера — Лемуса

Теорема: Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.

Доказательство 1: Пусть α > β, А L₁ = BL_2. Тогда 2α > α + β. Отложим от луча BL₂ в ту же полуплоскость, в которой лежит луч B С, угол α; N – точка пересечения биссектрисы А L₁ с этим лучом. Тогда А N > А L_1. Вокруг четырехугольника А L₂L₁B можно описать окружность. В ней α + β А N А L_1. Противоречие. Аналогично, получим противоречие, предположив, что α 2α = 2β => ВАС = АВС, что и требовалось доказать.

Теорема: Если две биссектрисы треугольника равны, то этот треугольник – равнобедренный.

Пусть в треугольнике АВС (см. рис. 18) , но а с. Рассмотрим и . Без ограничения общности можно считать, что а > c , тогда >

0,5 > 0,5 cos 0,5 cos 0,5 , так как эти углы – острые. Сравним: . Таким образом, , что противоречит условию. Следовательно, а = c , что и требовалось доказать.

2. Вычисления длины биссектрисы.

Теорема: Длина биссектрисы угла треугольника равна отношению удвоенного произведения сторон, образующих этот угол, помноженного на косинус половины угла, из которого она выходит, к их сумме.

Доказать: k =

Пусть AB = c , BC = a , AC = b , AK = k . ( рис №19) S Δ АВС = S Δ АВ K+ S Δ AK С ,

· sin A = · sin + · sin , так как sin A = 2 · sin · cos _. Отсюда следует

cb · sin · cos = · sin + · sin

2 bc · cos = k ( c + b ) отсюда получаем k = . Теорема доказана

Теорема: Квадрат длины биссектрисы угла треугольника равна разности произведений сторон, образующих этот угол, и отрезков, которые она образует при делении третьей сторону.

Дано: Δ АВС

Доказать: k 2 = bc – xy .

Пусть AB = c , BK = x , KC = y , AC = b , AK = k . По теореме косинусов

cos AKB = _, cos AKC = .

cos AMB = -cos AMC ( т . к . смежные ) => =

k 2 y + x 2 y — c 2 y = -k 2 x — y 2 x + b 2 x => k 2 y + k 2 x = b 2 x + c 2 y — x 2 y — y 2 x

_, (*)

(по теореме о пропорциональных отрезках)

Выполним подстановку в (*). И тогда получаем k 2 = bc – xy . Что и требовалось доказать.

Теорема: Пусть a , b , c – стороны треугольника, l _{a –} биссектриса к стороне a . Тогда

Пусть m = BL , n = LC , k = LM . Тогда m · n = l · k

Из подобия треугольников ABL и AMC имеем , т. е. l 2 _a = b · c — l _a · k . Отсюда

l 2 _a = b · c — m · n , Теорема доказана.

3. Занимательная информация о биссектрисе.

Мнемоническое (Мнемо́ника — греч. τα μνημονιχα — искусство запоминания), правило:

Биссектриса — это крыса, которая бегает по углам и делит угол пополам

В углу у кипариса, фактически, в тени,
влачила Биссектриса безрадостные дни.
— Ах, я иного круга! Я не халам-балам!
На что мне этот угол, деленный пополам?

Сумела исхитриться на дерзкие дела,
сбежала Биссектриса, осталась без угла.
Но долетели сплетни, что, якобы, она
в окружности соседней Диаметру жена.

Живет с улыбкой гордой в нездешней стороне.
Теперь зовется Хордой и счастлива вполне.
А я сижу, не евши, вдали от Биссектрис,
в углу осиротевшем несчастный кипарис.

Пью чай из барбариса, а сердце – просто хлам! —
разбито Биссектрисой, как угол, пополам.
Все будто бы в тумане и тенькает висок.
Схожу-ка к Медиане – развеюсь на часок!

Сказка о двух Углах и Биссектрисе, или Образование Смежного угла.

Было это или не было – не знаю. Однако расскажу вам историю, которую знает каждый малыш Геометрии и которую каждый служащий церквометрии переписывает, придя на службу.

А было всё так. Однажды на одной плоскости повстречались два Угла. Старший, которому было 130° (здесь год заменяется на 1°), и младший, которому от роду было лишь 50°. Встретились и тут же поспорили, кто из них важнее, лучше смелее. Младший утверждал, что сильнее, потому что он моложе, а сил, по его утверждению у него больше. Старший считал себя самым — самым, потому что он старший и много повидал за свои 130°. Спор уже не мог продолжаться, и они решили провести турнир.

О турнире знала Биссектриса, она и задумала победить двух своих врагов, и тем самым встать во главе Геометрии.

Начался турнир в назначенное время. На нём присутствовало два Угла. В самый разгар сражения вдруг появилась Биссектриса, застав бойцов в растерянности. В бой с Биссектрисой вступил старший Угол, затем младший, но к успеху это не привело. Победа, казалось, была на стороне Биссектрисы. Она торжествовала и уже представляла себя в роли правителя. Вдруг к Углам пришла идея. Они решили объединить силы и прогнать злодейку из страны.

Торжествующая Биссектриса не заметила, что вместо двух Углов, двух ярых противников, появился Смежный Угол, который в момент победил её. Биссектриса взмолилась опрощении. С тех самых пор Биссектриса находится на службе у короля, а два Угла, два ярых противника, стали одним целым Смежным Углом и находятся на службе у короля, защищая Геометрию от врагов.

Заспорили Стороны угла, никак между собой не поладят.

— Я, со своей стороны, считаю… — говорит одна Сторона.

— А я считаю, со своей стороны… — возражает ей другая.

Ничего не поделаешь: хоть у них и общий угол зрения, но смотрят-то они на мир с разных сторон!

Проходила как-то между ними Биссектриса. Обрадовались Стороны: вот кто будет их посредником! Спрашивают Биссектрису:

— А вы как думаете?

— А ваше мнение каково?

Стоит посредник посрединке, колеблется.

— Ну, скажите же, скажите! — тормошат Биссектрису со всех сторон.

— Я думаю, вы совершенно правы, — наконец произносит Биссектриса, кивая в правую сторону.

— Ах, какая вы умница! — восхищается правая Сторона. — Как вы сразу все поняли!

А Биссектриса между тем поворачивается к левой Стороне:

— Ваша правда, я тоже всегда так думала.

Левая Сторона в восторге:

— Вот что значит Биссектриса! Сразу сообразила, что к чему!

Стоит Биссектриса и знай, раскланивается: в одну сторону кивнет — мол, правильно, в другую сторону кивнет — мол, совершенно верно. Мнение Биссектрисы ценится очень высоко, поскольку оно устраивает обе стороны.

3. Геометрическая сказка.

Жила-была Биссектриса. Занималась своим прямым делом – делила углы пополам. Как только создадут две прямолинейности угол, она сразу туда – пополам делить и границы устанавливать. Иногда углы были достаточно острые, и Биссектриса натыкалась на них и больно кололась. А бывали углы настолько тупые, что даже делиться не хотели, ни пополам, ни в какой иной пропорции… Биссектрису такая работа очень утомляла, поскольку мало ей было места для творчества. Ничего другого, кроме углов и их разделения, жизнь такая от нее не ожидала. Она и книжки по геометрии читала, пытаясь найти себе другие применения. Она и с другими фигурами советовалась, как свойства свои и качества многогранные в рамках геометрических правил проявлять. Но правила были однозначны и не оставляли места для фантазии. А фигуры только надменно посмеивались над Биссектрисой и цитировали «параграф 2 пункт 4 Конституции Геометрического государства»: «Биссектриса – это такая крыса, которая бегает по углам и делит угол пополам. » А иные надменно выпячивали свои формы и многозначительно заявляли: «Каждая точка и линия имеет свое место и назначение. Функции заранее определены и назначены, и никто не может стать кем-то иным, если это не предусмотрено Генеральными чертежами». Некоторые даже открыто дразнили бедную Биссектрису: «Ты даже не фигура отдельная, а сплошная функция! Тебя же без угла не бывает, потому что тебе в другом месте назначения не придумали!»
Обидно стало Биссектрисе от надменности такой и неблагодарности. И захотела Биссектриса выйти за границы геометрии и стать Волшебной палочкой, которая сама себе и фея-крестная, и рисовалка — превращалка чудотворная. И стала она подпольным образом другие книжки читать: по физике квантовой, психологии трансперсональной да по мастерству волшебному. И стали эти книги к ней сами приходить, и идеи новые стали сами подсовываться. Идеи-то эти давно бродили грустно по Геометрическому государству и искали почвы креативной для роста и реализации. Но государство это было шибко «правильное» да «параграфное». Граждане его были по большей своей части инертны и стереотипны, и всякое такое считали «ересью негеометрической». Было, правда, несколько фигур на руководящих постах, которые в геометрию игрались, да не заигрывались, поскольку просветленные они были и практически сакральные. Они даже учение свое засекреченное имели – «Сакральная геометрия». Да только тайное это было общество, и простым фигурам, а тем более биссектрисам (которые даже и не фигуры, а так – палки-отмерялки) не было туда входу.
Но Биссектриса наша не отчаивалась. Да и в общества тайные посвящаться не стремилась. А стремилась она свойства свои расширить и качества проявить, про которые в учебниках по геометрии и написано-то не было. И однажды пришло ей письмо под грифом «секретно» от Сакрального Круга. Открыла она письмо это таинственное, а там – Указ высокий «об отмене ограничений функций и свойств данной Биссектрисы и наделении ее правом расти и развиваться в любом направлении, а также приобретения любых форм и размеров». И подпись – Круг (имя посвящения – Мандала). И стала она тренироваться и расти творчески. И вскоре прямолинейность ее превратилась в гибкость, она научилась сворачиваться в круг, закручиваться в спираль и складывать суставы в треугольник. А потом она попробовала вдохнуть и обрела объем, превозмогая свою двухмерность. От этого книга, в которой она жила, распахнулась, и бывшая биссектриса выкатилась на стол. Оглянулась она на государство свое и увидела, что это всего лишь книга, которая лежит среди других книг-государств. А кроме книг, есть еще множество других предметов, и все их необходимо изучить. И это ужасно интересно. И она, уже больше не биссектриса, вырастила себе крылья (а почему бы и нет?) и полетела в форточку – изучать огромный мир и себя в нем. Огромный мир был удивлен и обрадован появлению биссектрисы в таком качестве и принял ее в свое волшебное пространство с любовью и заботой. Когда ей хотелось быть Волшебной кистью – мир разворачивался в огромный холст и с удовольствием давал себя разноцветить. Когда она меняла форму и делала поверхность зеркальной – мир с удовольствием заглядывал в нее множеством лиц, мордочек и рожиц. Когда ей хотелось петь, и она превращалась в Голос – мир радостно подхватывал ее песню многократным эхо. А иногда ей даже хотелось на пять минут стать снова биссектрисой и поделить пару-тройку углов. И тогда мир раскрывался перед ней знакомой с рождения книгой, и она весело ползала по страничкам, играя в геометрию. Но теперь она помнила, Кто Она На Самом Деле…

4. Сказка о биссектрисе.

В некотором царстве, Треугольников государстве жил-был царь стороны той государь. Звали его Перпендикуляр, правил страною железной рукою, правильным считал только угол прямой, всех остальных по нему равнял, и никаких отклонений не признавал. Короче был деспот и тиран. Но за три тысячелетия существования планеты Геометрия, демократия и до страны Треугольников дошла, Перпендикуляр тут же перестроился. Вместо обращения “Ваше Перпендикулярное Высочество” позволил своим подданным величать себя, по-простецки, “Высота”.В какой бы треугольник Высота не приезжал, сразу из всех вершин восстанавливал, на прямую содержащую противоположную сторону, перпендикуляр и в точке их пересечения походный трон размещал. Больше всех обижал он треугольники тупоугольные. Вы правы. Кому же понравится, если Ваш почетный гость за тридевять земель от вашего замка в чистом поле расположился. Да и перед соседями стыдно. Прямые углы и тут в фаворе были, еще бы, его высочество в вершине прямого угла всегда останавливался, не зависимо от величины других углов и сторон прямоугольного треугольника. Остроугольные треугольники внимание на место расположения трона не обращали ввиду врожденного чувства юмора. И была у Перпендикуляра жена – Царица Медиана. В отличие от супруга доброй была, всех помирить стремилась, везде с мерною линейкою ходила, все стороны пополам делила. И была у них дочь – прекрасная Принцесса Биссектриса. Принцесса очень юной была, многого о жизни треугольников не знала, но была у нее заветная мечта все углы в их Царстве- государстве помирить, все конфликты разрешить, научиться углы поровну делить. Правда, задачу она себе посложнее матушкиной выбрала. Не всегда у нее градусы нацело делились, а с минутами в силу своего юного возраста Принцесса еще не разобралась. Но упрямства ей у папы занимать не приходилось, везде Биссектриса с транспортиром ходила, и все углы мерила, мерила, мерила…Вся жизнь в Царстве Треугольников была пронизана идеей равенства и братства. Был издан Свод законов, в котором основные определения и теоремы записаны были, и которым все жители страны неукоснительно следовали. Раз в неделю, по четвергам, царская семья собиралась на совет, на котором решала спорные вопросы, возникавшие в их стране. Пока царь с царицей судили да рядили своих подданных, коварная Баба Яга похитила Принцессу Биссектрису и заточила ее в башне в самом дальнем и неприступном углу царства Треугольников. Пыталась бежать из плена юная принцесса, но не смогла. Вокруг топи и болота непроходимые. Подсказал юной Биссектрисе выход ее верный друг Транспортир, что есть в том болоте тропинка неприметная, проходит она на равном расстоянии от сторон угла, только как разыскать ее, никому не ведомо. Биссектриса хоть и юною была, но не глупою, поняла Принцесса, что для своего спасения ей надо разделить угол ровно пополам. Измерила Принцесса угол и ахнула: 137 0 23’. Делила она и так и эдак, ничего не получается. Обиделась Принцесса на своего друга Транспортира и прогнала его. Узнал царь о случившейся беде и велел глашатым собирать народ на площади. Собралось народу видимо-невидимо. И велел им царь в путь дорогу собираться, царевну из плена выручать. А тому, кто Принцессу спасет, обещал пятерку золотом и ползачета в придачу. ( См. Презентация «Сказка о биссектрисе»)

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Биссектриса — свойства, признаки и формулы

Базовым понятием и одним из наиболее интересных и полезных объектов школьной математики является биссектриса. С её помощью доказываются многие положения планиметрии, упрощается решение задач.

Известные свойства позволяют рассматривать геометрические фигуры с разных точек зрения. Появляется вариативность при выборе пути доказательств.

Становится возможным использование инструмента алгебры, например, свойство пропорции, нахождение неизвестных величин, решение алгебраических уравнений при рассмотрении геометрических вопросов.

Видео:Свойство биссектрисы треугольника с доказательствомСкачать

Что такое биссектриса в геометрии

Рассматривают луч, выходящий из вершины угла или его часть (отрезок), который делит угол пополам. Такой луч (или, соответственно, отрезок) называется биссектрисой.

Часто для треугольников определение немного сужают, говоря об отрезке, соединяющем вершину угла, делящем его пополам, с точкой на противолежащей стороне. При этом рассматривается внутренняя область фигуры.

В то же время, часто при решении задач используются прямые, делящие внешние углы на два равных.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Биссектриса прямоугольного треугольника

Для прямоугольного треугольника одна из биссектрис образует равные углы, величины которых хорошо просчитываются (45 градусов).

Это помогает вычислять углы при решении задач, связанных с фигурами, которые можно представить в виде прямоугольных треугольников или прямоугольников.

В тупоугольном треугольнике биссектриса делит больший угол на равные части, величина которых меньше 90 0 .

Видео:3 свойства биссектрисы #shortsСкачать

Свойства биссектрисы треугольника

1. Каждая точка этой линии равноудалена от сторон угла. Часто эту характеристику выбирают в качестве определения, поскольку верно и обратное утверждение для любого произвольного треугольника. Это позволяет находить и радиус вписанной окружности.

2. Все внутренние отрезки, делящие углы пополам, пересекаются в одной точке, которая является центром окружности, вписанной в фигуру, т. е. точка пересечения находится на равных расстояниях от сторон.

Данное свойство позволяет решать целый класс разнообразных задач, выводить формулы для радиусов вписанных окружностей правильных многоугольников.

Благодаря этому утверждению, легко доказывается следующее правило:

Площадь описанного многоугольника равна:

где p – полупериметр, а r – радиус вписанной окружности.

Это позволяет находить решение не только планиметрических, но и стереометрических задач.

Важную роль играют внешние биссектрисы треугольника. Вместе с внутренними они образуют прямые углы;

3. Сумма величин двух прилежащих сторон, делённая на длину противолежащей стороны, задаёт отношение частей биссектрисы (считая от вершины), полученных точкой пересечения всех трёх соответствующих линий.

Некоторые виды геометрических фигур, в силу своих особенностей, порождают особые примечательные характеристики;

4. В равнобедренном треугольнике биссектриса, проведённая к основанию, одновременно является медианой и высотой. Две другие – равны между собой.

В этом случае основание параллельно внешней биссектрисе.

Обратное положение также имеет место. Если прямая проведена параллельно основанию равнобедренного треугольника через некоторую вершину, то внешняя биссектриса при этой вершине является частью этой линии;

5. Для равностороннего многоугольника важной характеристикой считается равенство всех биссектрис;

6. У правильного треугольника все внешние биссектрисы параллельны сторонам;

7. Выделяют несколько особенностей, среди которых есть следующая теорема:

«Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам».

Обратное утверждение («Прямая делит сторону на отрезки, пропорциональные двум другим сторонам») выражает признаки того, что рассматриваемая линия является внутренней биссектрисой;

8. Разносторонний треугольник позволяет определить взаимное расположение его высоты, медианы и биссектрисы, проведённых из одной точки. В частности, медиана и высота располагаются по разные стороны от третьей линии.

Видео:Секретные формулы биссектрисы треугольника!😉❤️‍🔥#математика #егэСкачать

Все формулы биссектрисы в треугольнике

В зависимости от исходных данных, длина биссектрисы, проведённой к стороне C, l_c, равна:

Видео:Формула для биссектрисы треугольникаСкачать

Примеры решения задач

Задача №1

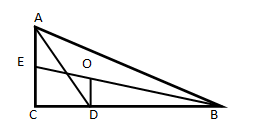
В ΔABC ∠C = 90°, проведена биссектриса острого угла. Отрезок, соединяющий её основание с точкой пересечения медиан, перпендикулярен катету. Найти углы заданной фигуры.

Пусть ∠ACB = 90°, AD – биссектриса, BE – медиана, O – точка пересечения медиан, OD⊥BC.

Тогда OE : OB = 1 : 2по свойству медиан.

Так как OD⊥BC, то ODIIOC, следовательно, ΔBOD ∼ ΔBEC по второму признаку подобия, поэтому, по свойству подобных фигур, CD : DB = 1 : 2.

Это означает, что CA : AB = 1 : 2.

Так как катет равен половине гипотенузы, то ∠ABC = 30°, откуда ∠CAB = 60°.

Задача №2

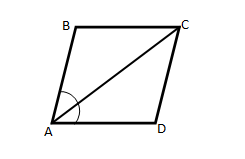
Диагональ параллелограмма делит его острый угол пополам. Доказать, что этот параллелограмм является ромбом.

Так как ABCD – параллелограмм, то ∠DAC = ∠ACB, как накрест лежащие при параллельных прямых AD, BC и секущей AC.

По условию, ∠DAC = ∠ACB = ∠BAC, поэтому ΔACB равнобедренный, то есть AB = BC, следовательно, ABCD – ромб.

Видео:Свойства биссектрисы треугольникаСкачать

Определение и свойства биссектрисы угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Видео:11 класс, 46 урок, Теорема о биссектрисе треугольникаСкачать

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Видео:Самые древние народы земли. Как жили бушмены и готтентоты // Дробышевский. Человек разумныйСкачать

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

• CD – внутренняя биссектриса ∠ACB;
• CE – биссектриса угла, смежного с ∠ACB;
• ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.

Видео:Свойство биссектрисы треугольникаСкачать

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

🔍 Видео

Теорема о биссектрисе угла треугольника | Осторожно, спойлер! | Борис Трушин |Скачать

АНТАРКТИДА - Тайна самого ЗАГАДОЧНОГО материка планетыСкачать

Биссектрисы треугольника.Скачать

ПОСТРОЕНИЕ БИССЕКТРИСЫ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Формула биссектрисы треугольникаСкачать

САМЫЕ Необычные Открытия Археологов, Которые Вас УдивятСкачать

СВОЙСТВО БИССЕКТРИСЫ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Пересечение биссектрис треугольника в одной точке, Геометрия 7 классСкачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

4 свойства биссектрисы треугольника для ЕГЭ! #ЕГЭ #ОГЭ #Математика #Skyeng_ExamsСкачать