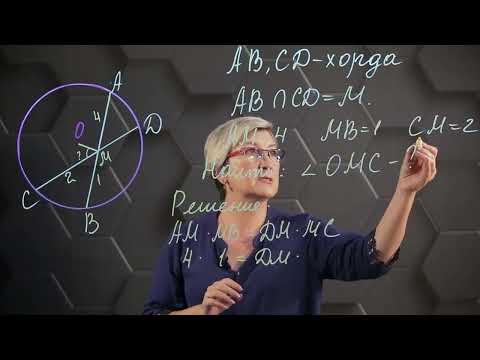Задачи на отрезки связанные с окружностью

Отрезки и прямые, связанные с окружностью. Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Свойства хорд и дуг окружности

Теоремы о длинах хорд, касательных и секущих

Доказательства теорем о длинах хорд, касательных и секущих

Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Фигура	Рисунок	Определение и свойства
Окружность
Круг
Радиус
Хорда
Диаметр
Касательная
Секущая

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды		Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности		Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Фигура	Рисунок	Теорема
Пересекающиеся хорды
Касательные, проведённые к окружности из одной точки
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

Практикум по геометрии на тему «Решение задач на отрезки в окружности». 8 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Геометрия 8 класс. Практикум «Решение задач на отрезки в окружности»

Учитель: Коряковцева Нина Владимировна

Целью проведения практикума является отработка навыков использования пропорциональных отрезков при вычислении длин хорд и касательных окружностей.

Практикум предполагает самостоятельную деятельность учащихся. Листы для практикума содержат основные соотношения и 6 задач для решения: задачи 1-5 базового уровня сложности, №5 – повышенного уровня.

Для оценки можно использовать следующие критерии: при решении 1-5 задач оценка «5», 1-4 – «4», 1-3 – «3». За решение задачи №6 можно поставить дополнительную оценку.

Краткое описание документа:

Целью проведения практикума является отработка навыков использования пропорциональных отрезков в окружности при вычислении длин хорд и касательных к окружности. Практикум предполагает самостоятельную деятельность учащихся. Листы практикума содержат основные соотношения (памятка) и 6 задач для решения.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 934 человека из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 312 человек из 67 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 688 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 490 261 материал в базе

Материал подходит для УМК

«Геометрия. 7-9 класс», Волович М.Б., Атанасян Л.С.

Глава 4. Окружность

Дистанционные курсы для педагогов

Другие материалы

• 01.04.2020
• 514

• 01.04.2020
• 892

• 01.04.2020
• 423

• 01.04.2020
• 403

• 01.04.2020
• 1465

• 01.04.2020
• 339

• 01.04.2020
• 422

• 31.03.2020
• 809

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 01.04.2020 430 —> —> —> —>
• DOCX 237.7 кбайт —> —>
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Коряковцева Нина Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 4 года
• Подписчики: 78
• Всего просмотров: 891606
• Всего материалов: 519

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

Число иностранных студентов в РФ увеличилось за три года

Время чтения: 1 минута

Более 800 вузов проведут прием через суперсервис

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

УрФУ возглавил рейтинг медиаактивности вузов

Время чтения: 1 минута

В Петербурге дали рекомендации по переводу школьников на дистант

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Углы и отрезки, связанные с окружностью

Просмотр содержимого документа
«Углы и отрезки, связанные с окружностью»

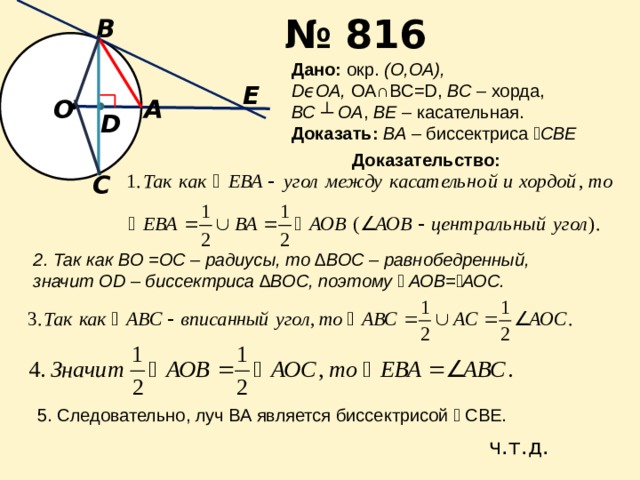
Углы и отрезки, связанные с окружностью

ВС ┴ ОА , ВЕ – касательная.

2. Так как ВО =ОС – радиусы, то ∆ВОС – равнобедренный,

значит OD – биссектриса ∆ВОС, поэтому ے АОВ= ے АОС.

5. Следовательно, луч ВА является биссектрисой ے СВЕ.

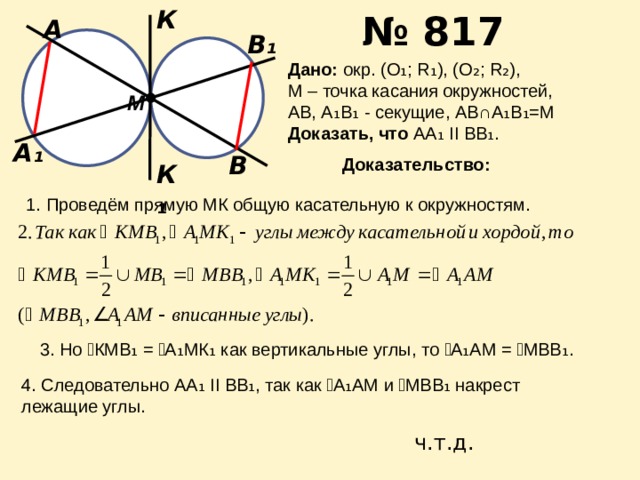
М – точка касания окружностей,

АВ, А₁В₁ — секущие, АВ∩А₁В₁=М

Доказать, что АА₁ II ВВ₁.

1. Проведём прямую МК общую касательную к окружностям.

3. Но ے КМВ₁ = ے А₁МК₁ как вертикальные углы, то ے А₁АМ = ے МВВ₁.

4. Следовательно АА₁ II ВВ₁, так как ے А₁АМ и ے МВВ₁ накрест

Дано: АС – касательная к окр. (О₁; R₁), BD – касательная к окр. (О₂; R₂)

Доказать, что а) AD II BC; б) AB² = AD · BC; в) BD² : AC² = AD : BC.

б) 3) ∆ABD ̴ ∆ABC по I признаку подобия треугольников, то

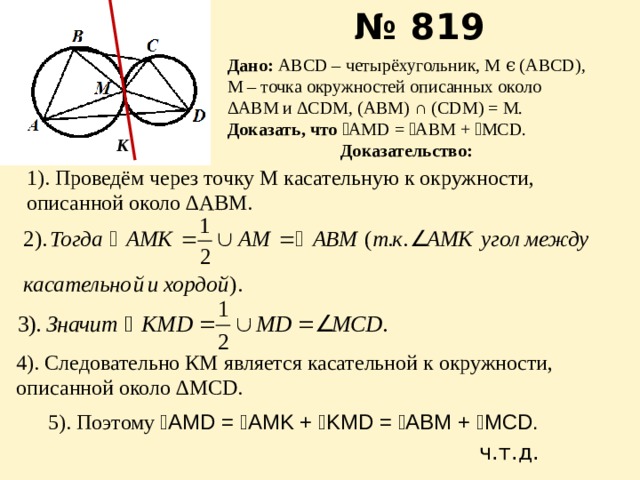
Дано: ABCD – четырёхугольник, М ϵ (ABCD),

М – точка окружностей описанных около

∆ АВМ и ∆CDM, (ABM) ∩ (CDM) = M.

Доказать, что ے AMD = ے ABM + ے MCD.

1). Проведём через точку М касательную к окружности, описанной около ∆АВМ.

4). Следовательно КМ является касательной к окружности, описанной около ∆MCD.

5). Поэтому ے AMD = ے AMK + ے KMD = ے ABM + ے MCD.

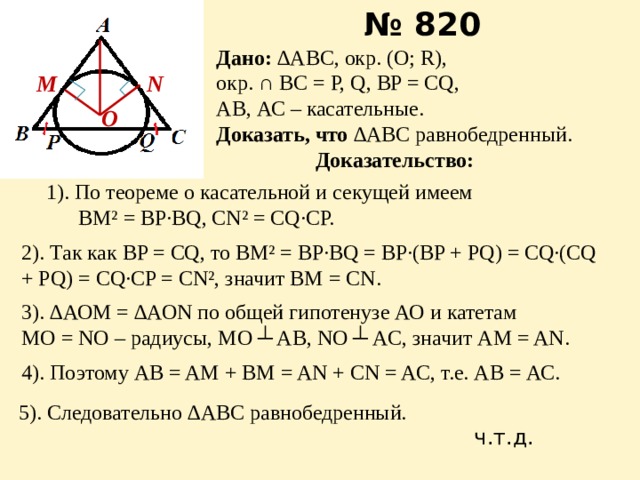
окр. ∩ BC = P, Q, BP = CQ,

АВ, АС – касательные.

Доказать, что ∆АВС равнобедренный.

1). По теореме о касательной и секущей имеем

ВМ² = ВР·BQ, CN² = CQ·CP.

2). Так как BP = CQ, то BM² = BP·BQ = BP·(BP + PQ) = CQ·(CQ + PQ) = CQ·CP = CN², значит ВМ = СN.

3). ∆АОМ = ∆АОN по общей гипотенузе АО и катетам

MO = NO – радиусы, MO ┴ AB, NO ┴ AC, значит AM = AN.

4). Поэтому AB = AM + BM = AN + CN = AC, т.е. АВ = АС.

5). Следовательно ∆АВС равнобедренный.

Дано: окр. (О; R), AB ∩ CD = E,

Доказать, что EC = EB или EC = EA, ED = EB или ED = EA.

1). По теореме о пересечения хорд имеем AE · EB = CE · DE.

2). Так как хорды AB = CD, то выразим DE через AB,

DE = AE + EB – CE, AE · EB = CE · (AE + EB – CE),

AE·EB = CE·AE + CE·EB – CE²,

AE·EB – CE·AE – CE·EB + CE² = 0,

AE·(EB – CE) – CE·(EB – CE) = 0, (EB – CE)·(AE – CE) = 0.

3). Значит либо EB – CE = 0 или либо AE – CE = 0.

4). Следовательно EB = CE или AE = CE, тогда EB = ED или EA = ED.

Дано: окр. (О; R), КА – хорда,

КВ – касательная, ОN ﬩ OA,

ON ∩ KA = M, OM ∩ KB = N.

Доказать, что NK = NM.

1). Так как ОК- радиус, КВ – касательная, то ОК ﬩ КВ и КА ∩ ON = M, значит ے NKM = 90 ° — ے AKO.

2). ∆АОМ – равнобедренный (ОА = ОК – радиусы), то ے ОКА = ے ОАК.

3). ∆АОМ, ے АОМ = 90 °, (ON ﬩ OA) , то ے АМО = 90 ° – ے МАО.

4). Значит ے NKM = ے AMO.

5). Но ے АМО = ے NMK как вертикальные углы, значит ے NKM = ے NMK.

6). Следовательно ∆KMN равнобедренный, а значит NK = NM.

Дано: окр. (О; R), АВ, АС, В ₁ С ₁ — хорды, АВ ∩ В ₁ С ₁ = М,

АС ∩ В ₁ С ₁ = N, ᴗАВ ₁ = ᴗ В ₁ В, ᴗ АС ₁ = ᴗ С ₁ С.

Доказать, что AM =AN.

2). Но ᴗАВ ₁ = ᴗ В ₁ В и ᴗ АС ₁ = ᴗ С ₁ С, значит ے АМС ₁ = ے ANB ₁ .

3). Следовательно ∆AMN равнобедренный, поэтому AM =AN.

Дано: окр. (О; R), А, В, С, D ϵ окр.,

ВМ – биссектриса ∆АВС, ВМ ϵ BD.

Доказать, что ے AMD = ے BAD.

1). Так как ВМ – биссектриса ∆АВС, то ے АВМ = ے МВС.

2). Так как вписанные углы ے DBC и ے DAC опираются на одну и ту же ᴗ СD, то ے DВC = ے DAС.

3). Следовательно ے АВМ = ے МВС = ے DAС.

4). Из теоремы о сумме углов ∆АMD и ∆ABD, имеем ے AMD = 180 ° — ے DAМ – ے МDA, ے BAD = 180 ° –

– ے ABD – ے BDA, т.е. ے BAD = 180 ° – ے DAM – ے MDA.

5). Следовательно ے AMD = ے BAD.

Дано: ∆АВС, АА ₁ , ВВ ₁ – высоты.

Доказать, что А, В, А ₁ , В ₁ ϵ окр. (О; R).

1). Возьмем точку К ϵ АВ, так что АК = КВ.

2). Так как ∆АВВ ₁ , ے В ₁ = 90 ° , то КВ ₁ = КА = КВ.

3). Так как у прямоугольного треугольника центр описанной окружности лежит на середине гипотенузы, т.е. в точке К, то точки А, В, В ₁ ϵ окр. (К; КВ ₁).

4). Так как ∆АВА₁, ے А ₁ = 90 ° , то КА ₁ = КА = КВ.

5). Значит точки А, В, А ₁ ϵ окр. (К; КА ₁).

6). Следовательно точки А, В, А ₁ , В ₁ ϵ окр. (К; КВ ).

Дано: АВСD – вписанный четырёхугольник, АС ﬩ ВD – диагонали.

Доказать, что AB² + CD² = BC² + AD² = d².

1). Обозначим ے CAD = φ, тогда ے ADB = 90° – φ.

3). Выразим и сложим АВ = 2Rcos φ , CD = 2Rsin φ, тогда AB² + CD² = 4R².

4). По теореме Пифагора из треугольников имеем AB² + CD² = (BK² + AK²) + (CK² + DK²) = (BK² + CK²) + (AK² + DK²) = BC² + AD² = 4R² = d².

📹 Видео