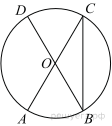- Задачи по геометрии для 7 класса по теме «Окружность» по материалам открытого банка заданий ОГЭ №17 и №25 демоверсии 2020
- Просмотр содержимого документа «Задачи по геометрии для 7 класса по теме «Окружность» по материалам открытого банка заданий ОГЭ №17 и №25 демоверсии 2020»
- Урок геометрии по теме «Окружность», 7 класс методическая разработка по геометрии (7 класс) на тему
- Скачать:
- Предварительный просмотр:
- Предварительный просмотр:
- Подписи к слайдам:
- 📸 Видео
Конспект урока
Окружность. Задачи на построение
Перечень рассматриваемых вопросов:
- Геометрическое место точек, примеры ГМТ.
- Изображение на рисунке окружности и ее элементов.
- Решение задач на построение.
- Выполнение построений прямого угла, отрезка, угла равного данному, биссектрисы угла, перпендикулярных прямых, середины отрезка с помощью циркуля и линейки.
Радиус окружности – отрезок соединяющий центр окружности с какой-либо точкой окружности.
Окружность – это геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Хорда – отрезок, соединяющий две точки окружности.
Диаметр – хорда, проходящая через центр окружности.
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М.А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М.А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Ранее мы узнали некоторые геометрические фигуры, например, угол, отрезок, треугольник, научились их строить и измерять. Сегодня мы введём определение ещё одной фигуры – окружности, рассмотрим её элементы и выполним построения геометрических фигур с помощью циркуля и линейки.
Для начала дадим определение геометрической фигуры, называемой окружностью.
Окружность – это геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Но можно использовать и другое определение окружности.
Окружность ‑ это геометрическое место точек, удалённых на одно и то же расстояние от точки, называемой центром окружности. Это расстояние называют радиусом окружности. В нашем случае точки О.
При этом стоит пояснить, что геометрическое место точек – это фигура речи, употребляемая в математике для определения геометрической фигуры, как множества всех точек, обладающих некоторым свойством.
Вспомним элементы окружности.
Радиус окружности – отрезок соединяющий центр окружности с какой-либо точкой окружности.
По определению окружности все её радиусы имеют одну и ту же длину. OM = OA
Отрезок, соединяющий две точки окружности, называется хордой.
Хорда, проходящая через центр окружности, называется диаметром.
O – середина диаметра.
Любые две точки окружности делят её на две части. Каждая из этих частей называется дугой окружности.
AMB, ALB – дуги окружности.
Построим окружность радиусом 3 см. Для этого поставим точку О. Возьмём циркуль и выставим с помощью линейки расстояние между ножками циркуля, равное 3 см. Поставим иголочку циркуля в точку О и построим окружность, вращая ножку циркуля с грифелем вокруг этой точки. Грифель описывает замкнутую кривую линию, которую называют окружностью.
Часть плоскости, которая лежит внутри окружности, вместе с самой окружностью, называют кругом, т. е. окружность ‑ граница круга.
Итак, мы можем с помощью циркуля строить окружность, но с его помощью можно построить и угол равный данному. Для построения воспользуемся ещё и линейкой.
Построить: EOМ = A.
1. Окр. (A; r), r – произвольный радиус.
2. Окр. (A; r) ∩ AB = B.
3. Окр. (A; r) ∩ AС = С.
4. Окр. (O; r) ∩ OM = D.
5. Окр. (D; BС) ∩ Окр. (O; r) = E
6. OЕ, ЕОD = BAC (из равенства ∆ОЕD и ∆ABC). EOM – искомый.
Теперь выполним построение биссектрисы угла.
Построить: AE – биссектриса CAB.
- Окр. (A; r), r – произвольный радиус.
- Окр. (A; r) ∩ AB = B.
- Окр. (A; r) ∩ AC = C.
- Окр. (C; CB) ∩ Окр. (B; CB) = E.
- AE – искомая биссектриса BAC, т. к. ABE =CBE (из равенства ∆ACE и ∆ABE).
Рассмотрим ещё одно построение с помощью циркуля и линейки. Построим середину отрезка АВ.
Для этого построим две окружности с центрами на концах отрезка , т. е. в точках А и В. Окружности пересекутся в точках Р и Q. Проведём прямую через точки Р и Q. Прямая РQ пересечёт прямую АВ в точке О, которая и будет являться искомой серединой отрезка АВ. Докажем это. Для этого рассмотрим ∆APQ и ∆BPQ. Они равны по трём сторонам, следовательно, ∠1 = ∠2, поэтому РО– биссектриса равнобедренного ∆АВР, а соответственно РО ещё и медиана. Следовательно, точка О – середина отрезка АВ.
Разбор заданий тренировочного модуля.
№ 1. АВ и СК – диаметры окружности, с центром в точке О. По какому признаку равенства треугольников равны треугольники АОС и ОКВ?
Так как О – центр окружности, то точка О делит диаметры пополам, следовательно отрезки АО, ОВ, ОС, ОК равны. ∠СОА = ∠КОВ (как вертикальные). Поэтому треугольники АОС и ОКВ равны по первому признаку равенства треугольников (по двум сторонам и углу между ними).
Ответ: 1 признак равенства треугольников.
№ 2. На рисунке O – центр окружности, АВ – диаметр окружности. Отрезки АD и ВС, перпендикулярны к отрезку АВ. АВ = 8 см, ОС = 5 см, СВ = 3 см. Чему равен периметр ∆AOD?
Периметр треугольника AOD равен сумме сторон АО, AD, DO. Найдём эти стороны.
По условию O – центр окружности, то она делит диаметр пополам, следовательно отрезок АО равен отрезку ОВ, т. е. АО = АВ:2 = 8 см :2 = 4 см.
По условию отрезки АD и ВС, перпендикулярны к отрезку АВ, следовательно ∠СВО = ∠ОАD = 90°, ∠АОD = ∠СОВ (как вертикальные). Поэтому ∆АОD = ∆СОВ (по 2 признаку равенства треугольников). Следовательно, AD = СВ = 3 см, DO = ОС = 5 см.
Р∆AOD = АО + AD + DO = 4 см + 3 см + 5 см = 12 см.
Видео:ОКРУЖНОСТЬ задачи на построение 7 класс АтанасянСкачать

Задачи по геометрии для 7 класса по теме «Окружность» по материалам открытого банка заданий ОГЭ №17 и №25 демоверсии 2020
В разработке представлена подборка задач для 7 класса по геометрии по теме «Окружность». Задания взяты из открытого банка заданий ОГЭ демоверсии 2020 (№17 и№25)
Просмотр содержимого документа
«Задачи по геометрии для 7 класса по теме «Окружность» по материалам открытого банка заданий ОГЭ №17 и №25 демоверсии 2020»
Задачи по теме « Окружность» 7 класс
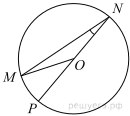
Найдите градусную меру ∠MON, если известно, NP — диаметр, а градусная мера ∠MNP равна 18°.
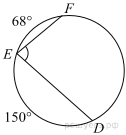
Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.
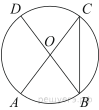
В окружности с центром O AC и BD — диаметры. Угол ACB равен 26°. Найдите угол AOD. Ответ дайте в градусах.
Точки A и B делят окружность на две дуги, длины которых относятся как 9:11. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.
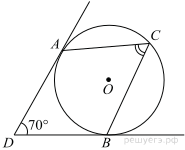
В угол величиной 70° вписана окружность, которая касается его сторон в точках A и B. На одной из дуг этой окружности выбрали точку C так, как показано на рисунке. Найдите величину угла ACB.
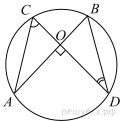
Величина центрального угла AOD равна 110°. Найдите величину вписанного угла ACB. Ответ дайте в градусах.
Точки A, B, C и D лежат на одной окружности так, что хорды AB и СD взаимно перпендикулярны, а ∠BDC = 25°. Найдите величину угла ACD.
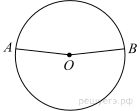
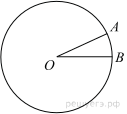
На окружности с центром O отмечены точки A и B так, что 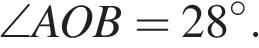
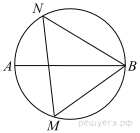
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA = 38°. Найдите угол NMB. Ответ дайте в градусах.
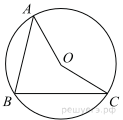
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC = 15° и ∠OAB = 8°. Найдите угол BCO. Ответ дайте в градусах.
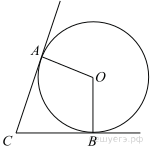
В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
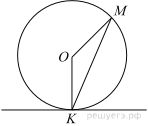
Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.
Касательные в точках A и B к окружности с центром O пересекаются под углом 72°. Найдите угол ABO. Ответ дайте в градусах.
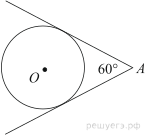
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Урок геометрии по теме «Окружность», 7 класс
методическая разработка по геометрии (7 класс) на тему
В данном материале представлана технологическая карта урока геометрии 7 класса по теме «Окружность», приложения к уроку, а также тест на знание теории в формате ОГЭ «Верно-неверно».
Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Скачать:
| Вложение | Размер |
|---|---|
| Технологическая карта урока «Окружность» | 68.58 КБ |
| Тест «Верно-неверно» | 1.12 МБ |
| Приложение 1 — задачи на урок | 71.9 КБ |
| Приложение 2 — рефлексия | 62.13 КБ |
Видео:№ 144 - Геометрия 7-9 класс АтанасянСкачать

Предварительный просмотр:
Всероссийский фестиваль педагогического творчества
(2015-2016 учебный год)
Номинация: Педагогические идеи и технологии: среднее образование
Автор: Васильева Светлана Алексеевна
Тема урока: ОКРУЖНОСТЬ.
- обучающие: повторить теоретический материал по теме «Окружность», закрепить признаки равенства треугольников; отрабатывать навыки использования признаков равенства треугольников при решении задач;
- развивающие: развивать логическое мышление, познавательный интерес, умение анализировать, наблюдать и делать выводы; развивать умение работать самостоятельно;
- воспитательные: формировать грамотную математическую речь, умение слушать, анализировать, умение чётко формулировать ответ на поставленный вопрос; формировать умение чётко распределять своё рабочее время на каждом этапе урока; формировать математическую культуру (оформление записей на доске и в тетради, использование математической символики и терминологии, использование чертёжных инструментов).
Технологическая карта урока
Тема урока, номер урока в теме
11 урок в теме «Треугольники».
Планируемые результаты урока
- определение окружности и ее элементов.
- определять элементы окружности;
- доказывать равенство треугольников и их элементов.
- полученные знания для решения задач.
1. рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности;
1. целеполагание – постановка учебной задачи
2. планирование – определение последовательности промежуточных целей (план, последовательность действий);
3. оценка – выделение и осознание учащимся того, что уже усвоено и что еще подлежит усвоению, оценивание качества и уровня усвоения;
1. умение предлагать и обосновывать своё мнение.
1. определять личностный смысл деятельности;
Основные понятия темы
Окружность, хорда, диаметр, радиус.
Применяемые современные технологии
Элементы технологии проблемного обучения.
Формы организации учебной деятельности
Этапы организации учебной деятельности
Содержание педагогического взаимодействия
Орг.момент – 1 мин.
Цель: Настроить учащихся на урок.
Устная работа – 9 мин.
Цель: проверить теоретические знания по теме «Треугольник».
Предлагает для устной работы тест «Верно-неверно».
Отвечают устно, комментируют свои ответы.
Мотивационный момент – 5 мин.
Цель: подвести учащихся к изучению темы.
Предлагает для прочтения текст:
«Это одна из древнейших геометрических фигур. В Древней Греции она считалась венцом совершенства. Действительно в каждой своей точке эта фигура “устроена” одинаково, что позволяет ей как бы двигаться “по себе”. На плоскости этим свойством обладает еще лишь прямая.
Представление об этой фигуре даёт линия движения модели самолёта, прикреплённого шнуром к руке человека, также обод колеса.
Для изображения этой фигуры необходим специальный чертежный прибор – циркуль.»
О какой геометрической фигуре идет речь в этом тексте?
Предъявлянет тему урока. Предлагает сформулировать цели урока.
Отвечают на вопрос.
Формулируют цели урока.
Новый материал – 7 мин.
Цель: вспомнить определение окружности и ее элементов.
Чит. П.21 учебника.
Задание 1: Вписать пропущенные слова в формулировки:
1. Геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки, называется ……
2. Отрезок, соединяющий центр окружности с какой-либо точкой окружности, называется …
3. Отрезок, соединяющий две точки окружности, называется…
4. Хорда, проходящая через центр окружности, называется…
5. Часть окружности, ограниченная двумя точками, называется …
Читают учебник, вписывают пропущенные слова в определение.
Решение задач – 20 мин.
Цель: применять признаки равенства треугольников при решении задач на окружность.
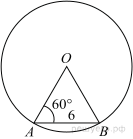
№ 4. Найти угол АОВ.
Решают задачи на листах по готовым чертежам.
Задание на самоподготовку – 1 мин.
Цель: прокомментировать задание на с/п.
Комментирует задание на самоподготовку:
- выучить определение окружности и ее элементов;
- решить задачи №144(в), 146, 147.
Записывают задание на самоподготовку.
Рефлексия – 2 мин.
Цель: Получить обратную связь, подвести итоги.
Задание: Соединить указанный элемент и рисунок, на котором он изображен.
Определяют указанные элементы на рисунке.
Предварительный просмотр:
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Подписи к слайдам:
Тест ВЕРНО — НЕВЕРНО
Определите: верно или неверно данное утверждение 1. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Определите: верно или неверно данное утверждение 2. Треугольник называется равнобедренным, если все его стороны равны.
Определите: верно или неверно данное утверждение 3. Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
Определите: верно или неверно данное утверждение 4. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника и точку противоположной стороны, называется биссектрисой треугольника.
Определите: верно или неверно данное утверждение 5. Если треугольники равны, то равны все их элементы.
Определите: верно или неверно данное утверждение 6. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники называются равными.
Определите: верно или неверно данное утверждение 7. Перпендикуляр, опущенный из вершины треугольника на противоположную сторону, называется высотой треугольника.
Определите: верно или неверно данное утверждение 8. Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Это одна из древнейших геометрических фигур. В Древней Греции она считалась венцом совершенства. Действительно в каждой своей точке эта фигура “устроена” одинаково, что позволяет ей как бы двигаться “по себе”. На плоскости этим свойством обладает еще лишь прямая. Представление об этой фигуре даёт линия движения модели самолёта, прикреплённого шнуром к руке человека, также обод колеса. Для изображения этой фигуры необходим специальный чертежный прибор – циркуль.
1. Геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки, называется … 2 . Отрезок, соединяющий центр окружности с какой-либо точкой окружности, называется … 3. Отрезок, соединяющий две точки окружности, называется… 4 . Хорда, проходящая через центр окружности, называется… 5 . Часть окружности, ограниченная двумя точками, называется … окружностью р адиусом окружности х ордой окружности д иаметром окружности д угой окружности
Доказать: AD = BC .
Доказать: АВ = ВС.
Окружность Центр окружности Хорда Диаметр Радиус Дуга окружности
📸 Видео
Окружность и задачи на построениеСкачать

Окружность. 7 класс.Скачать

7 класс, 21 урок, ОкружностьСкачать

Вся геометрия 7–9 класс с нуля | ОГЭ МАТЕМАТИКА 2023Скачать

ЗАДАЧИ НА ПОСТРОЕНИЕ 7 класс геометрия АтанасянСкачать

№ 150 - Геометрия 7-9 класс АтанасянСкачать

№ 147 - Геометрия 7-9 класс АтанасянСкачать

7 класс, 23 урок, Примеры задач на построениеСкачать

SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

Урок 3 Окружность и круг (7 класс)Скачать

Геометрия 7 класс, Урок 4, Окружности для чайников)Скачать

№ 145 - Геометрия 7-9 класс АтанасянСкачать

Геометрия 7 Примеры задач на построениеСкачать