Две плоскости пересеченные третьей по параллельным прямым параллельны между собой (5 видео)

Параллельность прямых и плоскостей

Содержание

Параллельные прямые
Признак параллельности прямых
Параллельные прямая и плоскость
Признак параллельности прямой и плоскости
Свойство прямой, параллельной данной плоскости
Параллельные плоскости
Признаки параллельности плоскостей
Свойства параллельных плоскостей
Свойства параллельных плоскостей
Параллельные плоскости и их свойства.
«Управление общеобразовательной организацией: новые тенденции и современные технологии»
🌟 Видео

Видео:№60. Две плоскости a и β параллельны плоскости γ. Докажите, что плоскости a и β параллельны.Скачать

Параллельные прямые

Параллельные прямые – прямые, которые лежат в одной плоскости и не пересекаются.

Признак параллельности прямых

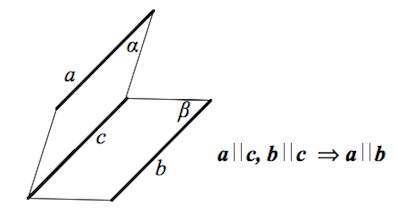
Две прямые, параллельные третьей, параллельны между собой.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Параллельные прямая и плоскость

Прямая и плоскость называются параллельными , если они не имеют общих точек.

Признак параллельности прямой и плоскости

Если прямая, не принадлежащая данной плоскости, параллельна какой-нибудь прямой этой плоскости, то она параллельна этой плоскости.

Свойство прямой, параллельной данной плоскости

Если плоскость β проходит через прямую a , параллельную плоскости α , и пересекает эту плоскость по прямой b , то b || a .

Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Параллельные плоскости

Параллельные плоскости – плоскости, которые не пересекаются.

Признаки параллельности плоскостей

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.

Если каждая из двух данных плоскостей параллельна третьей плоскости, то данные две плоскости параллельны между собой.

Свойства параллельных плоскостей

Если две параллельные плоскости пересекаются третьей плоскостью, то линии пересечения плоскостей параллельны.

Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:10 класс, 5 урок, Параллельность трех прямыхСкачать

Свойства параллельных плоскостей

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы рассмотрим три свойства параллельных плоскостей: о пересечении двух параллельных плоскостей третьей плоскостью; о параллельных отрезках, заключенных между параллельными плоскостями; и о рассечении сторон угла параллельными плоскостями. Далее решим несколько задач с использованием этих свойств.

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Параллельные плоскости и их свойства.

Видео:Параллельность прямых. 10 класс.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

С параллельными плоскостями мы встречаемся в жизни каждый день. Наиболее наглядный пример – это плоскости потолка и пола (если не брать в расчёт дизайнерские фантазии); это полки в шкафу; это плоскости ступеней (на которые мы наступаем), ну и т.д., и т.п.

Определение. Две плоскости в трёхмерном пространстве называются параллельными, если они не имеют общих точек.

На чертежах параллельные плоскости изображаются в виде одинаковых параллелограммов, которые смещены друг относительно друга, причём, если они расположены близко друг к другу, то не забывайте о невидимых линиях!

Определение. Две прямые в трёхмерном пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

ТЕОРЕМА (признак параллельности плоскостей). Если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости, то такие плоскости параллельны.

Доказательство. Предположим, что . Тогда одна из двух пересекающихся прямых или , лежащие в плоскости , пересекает прямую , которая также лежит в плоскости . Но, прямая , в то же время, лежит в плоскости , значит, одна из двух прямых или пересекает плоскость . Однако, по условию теоремы, , значит, (по признаку параллельности прямой и плоскости). Аналогично, , значит, . Мы пришли к противоречию с признаком параллельности прямой и плоскости вследствие того, что сделали изначально неверное предположение. Значит, , ч.т.д.

Свойства параллельных плоскостей.

ТЕОРЕМА 1 (о пересечении двух параллельных плоскостей третьей).

Если две параллельные плоскости пересекаются третьей плоскостью, то прямые пересечения плоскостей параллельны.

Поскольку , тогда прямые и либо пересекаются, либо параллельны. Но, кроме того, они лежат в параллельных плоскостях, т.е. не могут иметь общих точек. Значит, , ч.т.д.

ТЕОРЕМА 2 (о существовании и единственности плоскости, параллельной данной).

Через точку, расположенную вне данной плоскости, можно провести единственную плоскость, параллельную данной.

1. В данной плоскости проведём две пересекающиеся прямые (рисунок слева). Через данную точку проведём прямые и (это возможно сделать по аксиоме планиметрии: «через точку, не лежащую на прямой, можно провести прямую, параллельную данной, и, притом, только одну»). Через две пересекающиеся прямые и проведём плоскость . По признаку параллельности плоскостей, .

2. Докажем единственность существования такой плоскости. Предположим, что через точку проходит ещё одна плоскость , параллельная плоскости (рисунок справа). В плоскости проведём произвольную прямую через точку , а в плоскости отметим произвольную точку . Через прямую и, не лежащую на ней точку , можно провести плоскость , и, притом, только одну. Тогда . Так как (по построению) и (по предположению), то прямые и не пересекают прямую , т.е. и . Мы получили, что через точку в плоскости проходят две прямые и , параллельные одной и той же прямой . Это противоречит аксиоме планиметрии о параллельных прямых. Противоречие возникло вследствие неверного предположения. Значит, через точку вне плоскости можно провести только одну плоскость, параллельную данной, ч.т.д.

ТЕОРЕМА 3 (об отрезках параллельных прямых между параллельными плоскостями).

Отрезки параллельных прямых, отсекаемые параллельными плоскостями, равны между собой.

Так как прямые и параллельны, то через них можно провести плоскость . Тогда . Согласно теореме 1, . Значит, – параллелограмм. Т.к. у параллелограмма противоположные стороны равны, то , ч.т.д.

ТЕОРЕМА 4 (о транзитивности отношения параллельности плоскостей).

Если две различные плоскости параллельны третьей плоскости, то они параллельны между собой.

Предположим, что . Тогда , т.е. эти плоскости имеют общую точку. Значит, через одну точку проходят две плоскости и , параллельные одной и той же плоскости . А это противоречит теореме 2 о существовании и единственности плоскости, параллельной данной. Противоречие возникло вследствие неверного предположения, значит, , ч.т.д.