материал по математике (4 класс) на тему
Дополнение к открытому уроку математики в 4 классе — рабочий лист, самостоятельная работа, эталон.
Видео:Окружность. 7 класс.Скачать

Скачать:
| Вложение | Размер |
|---|---|
| etalon.doc | 27.5 КБ |
| samostoyatelnaya_rabota.docx | 248.45 КБ |
| rabochiy_list.docx | 44.37 КБ |
Видео:Математика. 4 класс. Окружность и круг /15.03.2021/Скачать

Предварительный просмотр:
Окружность – граница круга.
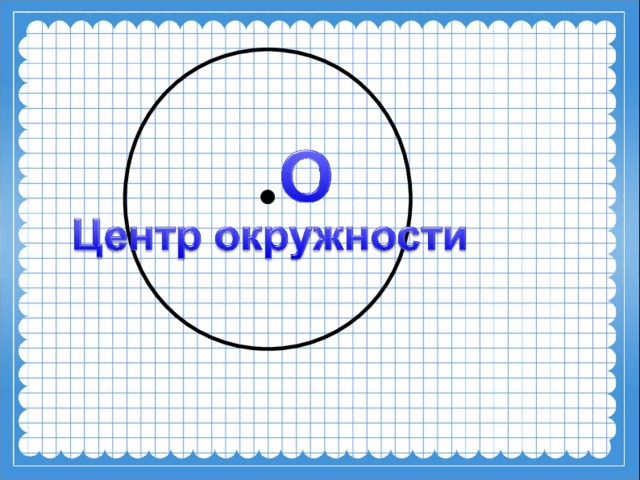
Точка О – центр окружности.
Отрезки ОА , ОВ , ОС – радиусы , отрезок АС – диаметр .
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Предварительный просмотр:
Самостоятельная работа
1)Проведите диаметр окружности МВ, измерьте его длину. Во сколько раз диаметр окружности меньше радиуса?
2) Измерь радиус каждой окружности и начерти окружности с такими же радиусами, но с центром в одной и той же точке О .
Видео:Задача для 4 класса, которую родители объясняют неправильно! | МатематикаСкачать

Предварительный просмотр:
Индивидуальный лист учени______4 А класса____________________________________
210 : 70 =_____ 90 ∙ 10 =________
30 ∙ 8 =_______ 300 : 10 =______
640 : 8 = _____ 49 ·10 =_________
1. Верите ли вы, что самая простая из кривых линий – окружность?
Верите ли вы, что самому старому обнаруженному циркулю более 2 тысяч лет?
3. Верите ли вы, что впервые термин “радиус” встречается лишь в 16 веке?
Верите ли вы, что цирк связан с циркулем?
Задание 3 (пробное действие) Задание 4 (работа по плану)
Постойте окружность и
проведите её радиус.
Задание 5(закрепление полученных знаний)
Начертите окружность радиусом 2 см. Отметьте центр окружности и проведите её радиус. Обозначьте точками. Проведите диаметр этой окружности, измерьте его длину. Во сколько раз диаметр окружности больше ее радиуса ?
Задание 6 (работа в парах)
А) Не нарушая закономерностей, Б) Выберите на рисунке ту окружность, в которой
построй радиусы в последних проведен диаметр.
Задание 7(учебник стр. 51 №8)
Индивидуальный лист учени______4 А класса____________________________________
280 : 40 =_____ 40 ∙ 10 =_____
40 ∙ 7 =_____ 50 ∙ 9 =_____
630 : 7 =_____ 480: 10 =_____
1. Верите ли вы, что самая простая из кривых линий – окружность?
Верите ли вы, что самому старому обнаруженному циркулю более 2 тысяч лет?
3. Верите ли вы, что впервые термин “радиус” встречается лишь в 16 веке?
Верите ли вы, что цирк связан с циркулем?
Задание 3 (пробное действие) Задание 4 (работа по плану)
Постойте окружность и
проведите её радиус.
Задание 5(закрепление полученных знаний)
Начертите окружность радиусом 2 см. Отметьте центр окружности и проведите её радиус. Обозначьте точками. Проведите диаметр этой окружности, измерьте его длину. Во сколько раз диаметр окружности больше ее радиуса ?
Задание 6 (работа в парах)
А) Не нарушая закономерностей, Б) Выберите на рисунке ту окружность, в которой
построй радиусы в последних проведен диаметр.
Задание 7(учебник стр. 51 №8)
Видео:Радиус и диаметрСкачать

По теме: методические разработки, презентации и конспекты
Рабочие листы по математике 1-й класс
Материал для отработки вычислительных навыков в 1 классе.
Рабочий лист ученика
Задания для обучающихся по русскому языку на повторение и обобщение знаний о предложении,связи слов в предложении.
Рабочий лист ученика
Рабочий лист ученика к уроку математики в 3 классе по теме : «Решение задач на движение».
Рабочий лист ученика 4класс Нахождение площади прямоугольного треугольника.
Рабочий лист соответствует требованиям ФГОС.
Рабочий лист по окружающему миру 1 класс
Рабочий лист по окружающему миру для 1 класса на тему: «Помоги птицам змиой".
Рабочий лист по внеклассному чтению 1 класс
Рабочий лист по внеклассному чтению для 1 класса.
Рабочий лист по литературному чтению 3 класс (И.Никитин «Встреча зимы»)
В рабочем листе представлена краткая биография автора, разбор стихотворения средствами художственной выразительности, историческая справка о празднике встречи зимы на Руси.
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Урок математики по теме «Периметр. Длина окружности». 4-й класс
Класс: 4
Тип урока: урок открытия новых знаний.
Цели:
- Дидактические:
- повторить и расширить знания о периметре многоугольников с учётом их свойств;
- дать понятие длины окружности и способов её нахождения;
- Развивающие:
- развивать логическое мышление, умение выделять главное, исследовательские и практические умения учащихся;
- расширять кругозор;
- Воспитательные:
- воспитывать любознательность, интерес к предмету.
Оборудование: индивидуальные листы с заданиями для учащихся; набор геометрических фигур для практической деятельности, нитки, стакан (любой), мультимедийная установка, экран, компьютер
I. Оргначало
– Хотела сказать: «Здравствуйте, дети!»
– Но, думаю: «А ведь нам предстоит решать такие проблемы, какие и не каждому взрослому под силу!»
– Предлагаю серьёзно и плодотворно поработать.
II. Актуализация опорных знаний. Постановка проблемы
Я предлагаю вам игру:
Пред вами ряд фигур
Внимательно на них взгляните
И на группы разделите
Предложения учащихся по способу разбиения:
– Назовите отличительные особенности каждой группы
– Выделим границы каждой фигуры.
– Как по-другому можно назвать границу многоугольника? (Периметр)
– Нужно ли нам знать понятие периметра и способ его нахождения? Обоснуйте своё мнение, приведите примеры. (Плинтус, оконные рамы, рамки картин и портретов, ограды участков, зданий и т.д.)
III. Постановка цели урока
– Решим практическую задачу:
«В парке решили разбить цветочные клумбы в виде различных геометрических фигур и выложить декоративной кирпичной кладкой бордюр. Сколько таких кирпичей понадобится для каждого бордюра, если на 1 м их необходимо 10 штук».
? – Как найти периметр бордюра каждой клумбы?
Закрепление способов нахождения периметра многоугольников с учётом их свойств, соответствующих формул, которые учащиеся записывают на доске:
Pкв. = a * 4 Pпр. = (a + b) * 2 Ррб.тр. = a * 2 + b
Ррв.тр. = a * 3
– Какая возникла проблема?
?! (Длину бордюра прямоугольника, квадрата и треугольников мы нашли, а вот длину бордюра клумбы круглой формы не умеем)
– Что является границей круга? (Окружность).
– Что нам сегодня предстоит выяснить? Какую цель для себя поставим? (Научиться находить длину окружности)
ТЕМА Периметр. Длина окружности.
ЦЕЛЬ Научиться находить длину окружности.
IV. Открытие нового
– Какие есть гипотезы?
– У меня в руках стакан и нитка. Какую форму имеет граница стакана? (Окружность)
– Как же можно использовать нитку, чтобы измерить длину данной границы? (Предложение учащихся: выложить нитку по границе поверхности стакана, отмерить, измерить по линейке)
?! – А как измерить длину окружности на плоскости?
– Давайте проведём исследование.
– Возьмите из набора фигур круг.
– Длину его окружности можно измерить, «прокатив» его по линейке. Но для начала нам необходимо знать, чему равна длина диаметра.
Диаметр – отрезок, соединяющий две точки окружности и проходящий через её центр.
– Как провести диаметр? Ваши предложения? (Перегнуть круг пополам, полученная линия сгиба и есть диаметр)
– Чему равен диаметр данной окружности? (9 см)
Учитель демонстрирует, как можно «прокатить» окружность вдоль линейки. Ребята проводят исследование.
– Что получилось? (Разные результаты. Приблизительно 28 см)
– Какой можно сделать вывод о практическом использовании данного способа? (Он неудобный, неточный)
– Продолжим исследование.
– Какие ещё геометрические фигуры есть у вас в наборе?
– Чем они интересны? (Эти многоугольники – треугольник, квадрат, восьмиугольник, шестнадцатиугольник – равносторонние)
– Подумайте, как можно использовать данные фигуры, чтобы найти длину окружности. (Предложения учащихся)
Если возникнут трудности, учитель подводит ребят наводящими вопросами:
– Какие фигуры можно назвать вписанными в окружность? (Фигуры, вершины которых принадлежат данной окружности)
– Попробуйте, используя модели фигур, «вписать» каждую в окружность. Что заметили? (Вписанные многоугольники тоже могут помочь определить длину окружности, причём, чем больше углов, тем фигура более приближена к границам окружности)
– Как вычисляли? (Сторона многоугольника, который мы выбрали – 2 см. Умножаем на количество сторон)
– Чему же равна длина окружности в этом случае? (32 см)
– Всё ли нас с вами устраивает? (Длина окружности установлена нами не точно, а, значит, расчёт необходимого материала может быть неправильным)
– Давайте рассуждать. Нам необходим более рациональный способ.
– Как вычисляли длину границы прямоугольника, квадрата, треугольника? (По формулам).
– Как думаете, есть ли формула, с помощью которой можно вычислить длину окружности?
(Предположения учащихся)
– Проведём ещё одно исследование.
– Внесём полученные в ходе нашего исследования данные в таблицу, где:
l – длина окружности
d – диаметр данной окружности и установим их соотношение, т.е. Вов сколько раз длина больше диаметра
– Вы видите, что результат во всех трёх случаях приблизительно равен 3.
– Вот так и было открыто волшебное число π ≈ 3,14, с которым более подробно вы познакомитесь в старших классах.
– Мы же с вами будем считать, что:
π ≈ 3
l : d = π,
– Значит, чтобы найти l, что нужно сделать?
| l = πd |
– Радиус – половина диаметра: d = 2r.
– Как эту же формулу можно записать по-другому?
| l = 2 π r |
– Мы сейчас с вами совершили открытие. Сделали это практически так же, как это было сделано ещё тысячи лет назад.
СЛАЙД 1
В древности самым известным государством был Вавилон.
СЛАЙД 2
Около 6 тысяч лет назад в Вавилоне было сделано замечательное открытие: люди изобрели колесо.
СЛАЙД 3
Вавилонские воины на боевых колесницах, запряжённых лошадьми, легко побеждали пеших врагов.
СЛАЙД 4
Вавилонские горшечники стали делать на горшечном круге красивую круглую посуду с тонкими стенками, которую охотно покупал не только в Вавилоне, но и в других странах.
(иллюстрация)
СЛАЙД 5
Водоподъёмное колесо подавало воду в водопровод, откачивало воду из рудников, орошало поля.
СЛАЙД 6
Не удивительно, что вавилонские учёные старательно изучали свойства окружности – колёсного обода. Вот как они измеряли длину окружности.
(фигуры в каждом рисунке «выплывают» последовательно)
СЛАЙД 7
Окружность – это своего рода «колесо геометрии». Одно из свойств колеса – его ось – остаётся всё время на неизменном расстоянии от поверхности, по которой оно катается.
Радиус – отрезок, который соединяет центр с любой точкой на окружности. В переводе с латинского радиус – «спица колеса».
СЛАЙД 8
Для вычисления длины окружности достаточно знать, во сколько раз окружность длиннее диаметра. Отношение этих длин обозначается буквой ? (пи). Вавилонские учёные принимали ? равным 3,14159…
– Мы прикоснулись с вами лишь на миг к великой мировой истории, её замечательным достижениям и открытиям.
V. Закрепление пройденного
– Чтобы ещё раз убедиться в необходимости полученных на уроке знаниях для решения практических задач предлагаю подумать вот над чем:
«На спортивной площадке выделили территорию круглой формы для метания мяча. Её необходимо обнести специальным ограждением. Чему будет равна длина данного ограждения?»
– Перед вами план площадки (работа в паре)
– Есть решение?
– Мы знаем формулу, по которой можно найти длину окружности. Что необходимо знать для решения задачи? (Диаметр)
– Каким образом находили его в прошлый раз? (Перегибанием)
– В данном случае подобный способ возможен? Как же быть?
(Учащиеся должны обратить внимание на то, что даны стороны прямоугольной площадки. Ширина площадки равна диаметру окружности, что видно по плану)
l = ? * d, l ? 3 * 12 = 36 (м)
VI. Домашнее задание (дифференцированное)
– У вас на листах есть задания для индивидуальной работы дома. Я предлагаю вам выбрать любое из них, в зависимости от того, какое вам покажется наиболее интересным. Попробуйте свои силы.
1. Найти длину окружности, используя рисунок:
2. Найти, чему равна длина беговой дорожки стадиона
VII. Итог
– Мы с вами – творцы! По-своему, первооткрыватели!
– Почему нас можно так назвать? (Мы нашли целых 3 способа вычислить длину окружности, вывели формулу)
– Я благодарю всех вас за прекрасную работу на уроке. Особенно хочу отметить смелость решений, творчество, инициативность.
– Но вы и сами можете оценить свою работу на уроке.
– Перед вами табличка:
Умения
Узнавать и называть фигуры
Вычислять периметр фигур с помощью изученных формул
Использовать формулу длины окружности
Решать задачи практического характера
– Изобразите в каждом столбце смайлик, в зависимости от того, насколько хорошо вы владеете данным умением.
– Закончить наш с вами урок я хотела бы так:
– Представьте себе, что мы все взялись за руки и образовали большой дружный круг.
– Чему будет равна длина окружности, которая у нас получилась?
Вытянутые руки – сажень, старинная русская мера длины, равная 2м 13 см (размах обеих рук взрослого человека)
– Значит, берём приблизительно 2 м.
– Что получилось?
– Ещё раз спасибо. Желаю вам удачи и новых открытий!
Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

«Окружность. Круг.»
Математику учить затем надо, что она ум в порядок приводит. М.В. Лормомносов.
Просмотр содержимого документа
«»Окружность. Круг.»»
Урок математики по теме: «Окружность. Радиус. Диаметр. » 4 класс
Составила: учитель начальных классов
МБОУ «Школы № 10 города Благовещенска»
Ивдра Анастасия Сергеевна
«Математику уже затем учить надо, что она ум в порядок приводит». М.В.Ломоносов
Игра «Верю – не верю»
1. Верите ли вы, что самая простая из кривых линий – окружность?
2.Верите ли вы, что самому старому обнаруженному циркулю 2 тысячи лет?
3. Верите ли вы, что впервые термин “радиус” встречается лишь в 16 веке?
4.Верите ли вы, что цирк связан с циркулем?
Циркуль – чертёжный инструмент.
ПРАВИЛА РАБОТЫ С ЦИРКУЛЕМ
1. Не держи циркуль концами вверх. 2. Не оставляй циркуль раскрытым. 3. Передавай циркуль закрытым, тупым концом вперед. 4. Работай аккуратно! Будь внимателен!
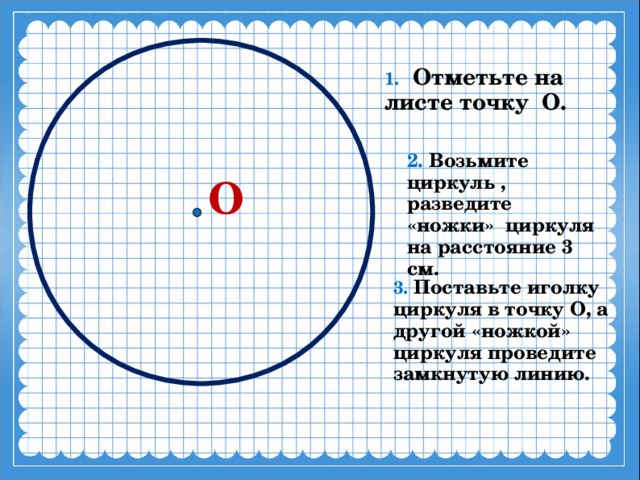
- Отметьте на листе точку О.
- Возьмите циркуль, разведите «ножки» циркуля на заданном расстоянии.
- Поставьте иголку циркуля в точку О, а другой «ножкой» циркуля проведите замкнутую линию.
- Начерти радиус.
1. Отметьте на листе точку О.
2. Возьмите циркуль , разведите «ножки» циркуля на расстояние 3 см.
3. Поставьте иголку циркуля в точку О, а другой «ножкой» циркуля проведите замкнутую линию.
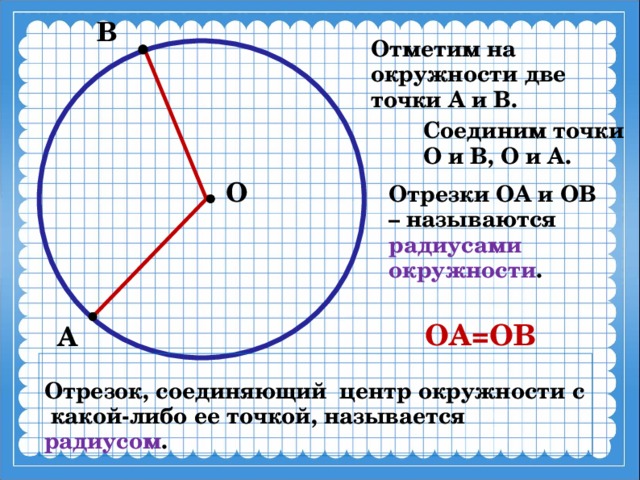
Отметим на окружности две точки А и В.
Соединим точки О и В, О и А.
Отрезки ОА и ОВ – называются радиусами окружности .
Отрезок, соединяющий центр окружности с какой-либо ее точкой, называется радиусом .
Сравните радиус окружности и её диаметр.
Отрезок, который соединяет две точки окружности и проходит через её центр, называется диаметром .
1.Начертите окружность радиусом 2 см.
2.Отметьте центр окружности и проведите её радиус. Обозначьте точками.
3.Проведите диаметр этой окружности, измерьте его длину.
4.Во сколько раз диаметр окружности больше ее радиуса ?
Не нарушая закономерностей, построй радиусы в последних окружностях:
Выберите на рисунке окружность, в которых проведен диаметр .
Проведите диаметр окружности МВ, измерьте его длину. Во сколько раз диаметр окружности меньше радиуса?
1. Верите ли вы, что самая простая из кривых линий – окружность?
2.Верите ли вы, что самому старому обнаруженному циркулю 2 тысячи лет?
3. Верите ли вы, что впервые термин “радиус” встречается лишь в 16 веке?
4.Верите ли вы, что цирк связан с циркулем?
Сегодня на уроке я узнал… Мне понравилось…. Было интересно….
🎥 Видео
Задачи по математике 4 класс. Как научиться решать задачи в 4 классе?Скачать

Математика. 4 класс. Окружность и круг. Обобщение /18.03.2021/Скачать

Окружность. Вебинар | МатематикаСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

Как решать задания на окружность ОГЭ 2021? / Разбор всех видов окружностей на ОГЭ по математикеСкачать

Окружность. Как найти Радиус и ДиаметрСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Математика 4 класс 123 урок. Окружность и кругСкачать

Задача на логику как отмерить 4 литра воды, которую решит не каждыйСкачать

Окружность и круг, 6 классСкачать

ОКРУЖНОСТЬ и КРУГ. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ. Контрольная №4. 7 классСкачать

Задача, которую боятсяСкачать