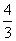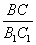Вы будете перенаправлены на Автор24
- Параллельный перенос
- Поворот
- Готовые работы на аналогичную тему
- Примеры задач на параллельный перенос и поворот
- Параллельный перенос, поворот плоскости и подобные треугольники
- Корзина
- Параллельный перенос
- Поворот плоскости вокруг точки на угол
- Подобные треугольники
- Урок по теме «Решение задач по теме «Движение»
- I. Орг.момент
- II. Проверка домашней работы
- III. Устная работа
- IV. Решение задач
- V. Подведение итогов урока
- 🎬 Видео
Видео:9 класс, 32 урок, Параллельный переносСкачать

Параллельный перенос
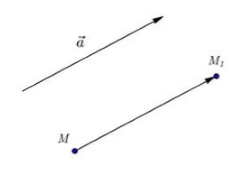
Введем определение параллельного переноса на вектор. Пусть нам дан вектор $overrightarrow$.
Рисунок 1. Параллельный перенос
Введем следующую теорему.
Параллельный перенос является движением.
Доказательство.
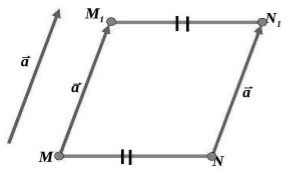
Пусть нам даны точки $M и N$. Пусть при их параллельном переносе на вектор $overrightarrow$ эти точки отображаются в точки $M_1$ и $N_1$, соответственно (рис. 2).
Рисунок 2. Иллюстрация теоремы 1
Значит четырехугольник $_1N_1N$ — параллелограмм и, следовательно, $MN=M_1N_1$. То есть параллельный перенос сохраняет расстояние между точками. Следовательно, параллельный перенос является движением.
Теорема доказана.
Видео:Геометрия 9 класс (Урок№29 - Параллельный перенос.)Скачать

Поворот
Введем определение поворота вокруг точки $O$ на угол $alpha $.
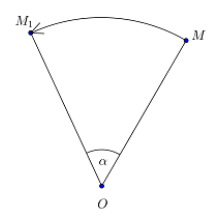
Поворот вокруг точки $O$ на угол $alpha $ — отображение плоскости на себя, при котором любая точка $M$ отображается на точку $M_1$ такую, что $_1=OM, angle M_1=angle alpha $ (Рис. 3).
Рисунок 3. Поворот
Готовые работы на аналогичную тему
Введем следующую теорему.
Поворот является движением.
Доказательство.
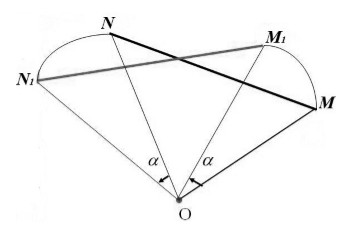
Пусть нам даны точки $M и N$. Пусть при их повороте вокруг точки $O$ на угол $alpha $ они отображаются в точки $M_1$ и $N_1$, соответственно (рис. 4).
Рисунок 4. Иллюстрация теоремы 2
Так как, по определению 2, $_1=OM, _1=ON$ и $overrightarrow<_1>=overrightarrow$, а ,$angle MON=angle M_1ON_1$, то
Следовательно, $MN=M_1N_1$. То есть поворот сохраняет расстояние между точками. Следовательно, поворот является движением.
Теорема доказана.
Видео:ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС И ПОВОРОТ 9 класс геометрия АтанасянСкачать

Примеры задач на параллельный перенос и поворот
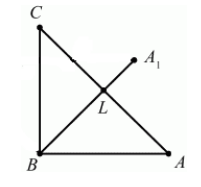
Построить треугольник $A_1B_1C_1$,образованный поворотом вокруг точки $B$ на угол $^0$ равнобедренного прямоугольного (с прямым углом $B)$ треугольника $ABC$.
Решение.
Очевидно, что точка $B$ перейдет сама в себя, то есть $B_1=B$. Так как поворот производится на угол, равный $^0$, а треугольник $ABC$ равнобедренный, то прямая $BA_1$ проходит через точку $L$ — середины стороны $AC$. По определению, отрезок $BA_1=BA$. Построим его (Рис. 5).
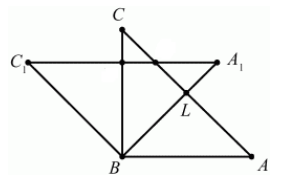
Построим теперь вершину $C_1$ по определению 2:
[angle CBC_1=^0, BC=BC_1]
Соединим все вершины треугольника $A_1B_1C_1$ (Рис. 6).
Решение закончено.
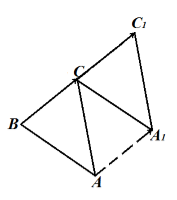
Построить параллельный перенос треугольника $ABC$ на вектор $overrightarrow$.
Решение.
Перенесем каждую вершину треугольника на вектор $overrightarrow$. Получаем треугольник $CA_1C_1$ (рис. 7).
Решение закончено.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 15 04 2021
Видео:Параллельный переносСкачать

Параллельный перенос, поворот плоскости и подобные треугольники
Корзина

Теоретический урок по предмету математики для решения задач по теме «Параллельный перенос, поворот плоскости и подобные треугольники».
Содержание данной онлайн страницы электронного справочника для школьников:
- – тема «Параллельный перенос» представлена на примере решения задач 145 — 148;
- – в контрольных работах с номерами 149 — 154 данной рабочей тетради по математике рассматривается поворот плоскости вокруг точки на угол;
- – повторение курса геометрии 9 класса в решениях приведено на примере заданий 155 — 173: углы треугольника, площадь треугольника через катеты и гипотенузу, вычисление радиуса описанной окружности, стороны ромба, подобные треугольники.
Видео:Параллельный перенос точки, отрезка, треугольника, четырехугольника. Геометрия 8 классСкачать

Параллельный перенос


Параллельным переносом на вектор 


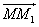

Задача 145.



A → A1 : 


B → B1 : 


Теорема:
При параллельном переносе на вектор 

f – параллельный перенос на вектор 
M 

N 



Точка M переводится движением в точку M1 с условием, что два вектора равны: M 



Точка N переводится движением в точку N1 с условием, что два вектора равны: N 



Следовательно, полученные отрезки параллельны MM1 || NN1 и построенные отрезки равны MM1 = NN1
Значит, четырехугольник MM1N1N – параллелограмм.
Поэтому MN = M1N1, значит f – движение.

Задача 146.
A 




B 




C 


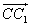


A 




B 




C 


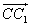



Задача 147.
точка D лежит на AC: D 
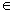
точка C лежит на AD: C 
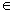
BC 
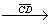
б) Доказать: ABB1D – равнобедренная трапеция
1) От точки B проведем прямую a, параллельную вектору 
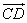

2) Точка B переводится движением в точку B1



3) Проведем прямую B1D, параллельную отрезку BC:
Рассмотрим четырехугольник BB1DC.
Т.к. основания BB1 || CD и боковые стороны BC || BD параллельны, то BB1DC – параллелограмм (по определению)
По свойству параллелограмма:
основания BB1 = CD и боковые стороны BC = BD равны, но AB = BC, тогда AB = B1D
Т.к. BB1 || AD параллельны и AB 
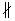
Т.к. AB = B1D, то ABB1D – равнобедренная трапеция.
Задача 148.
Дано: 
вектор 
окр (O;R) 

ΔABC 

EFPQ 

как показано на рисунке.
Видео:11 класс, 12 урок, Параллельный переносСкачать

Поворот плоскости вокруг точки на угол
Определение:




O – центр поворота
α – угол поворота
Задача 149.


α = 75° (против часовой стрелки)
O – центр поворота
1) A 
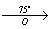


2) B 
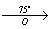


Теорема:
Поворот является движением.


α – угол поворота (против часовой стрелки)
точка O – центр поворота
Тогда треугольники равны ΔOMN = ΔOM1N1 по двум сторонам и углу между ними:




Тогда MN = M1N1, значит, f – движение.
Задача 150.
точка O – центр поворота


1) A 
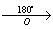


2) B 
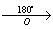


Задача 151.
точка A – центр поворота
α = 160° (против часовой стрелки)
1) B 
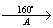


2) C 
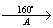


Задача 152.
точка O – центр поворота


1) A 
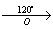


2) B 
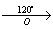


Задача 153.
точка C – центр окружности (C; R)
точка O – центр поворота
угол поворота α = 60° (против часовой стрелки)
а) точка C и точка O не совпадают
б) точка C и точка O совпадают


1) проведем луч CO
2) C 
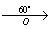



Т.к. точка О – центр поворота и точка С – центр окружности совпадают, то окружности (C;R) и (C1;R) будут тоже совпадать.

Задача 154.
Δ ABC – равнобедренный, равносторонний
D – точка пересечения биссектрис
D – центр поворота
угол поворота α = 120°
ΔABC 

Т.к. Δ ABC – правильный, то все углы в нем равны 60°.
Т.к. точка D – центр описанной и вписанной окружности, то
Δ ABD = Δ BDC = Δ DAC (по трем сторонам).
Следовательно, что 





A 

B 

C 

Таким образом, Δ ABC отображается на себя.
Повторение.
Задача 155.






Найти: наибольший угол треугольника
Пусть x – коэффициент пропорциональности. Зная, что сумма углов в треугольнике равна 180°, составим и решим уравнение:
3x + 7x + 8x = 180
Наибольший угол 

Задача 156.
треугольник ΔABC – равнобедренный,
один угол больше другого:






Найти: угол при основании треугольника
Пусть x° – угол при основании треугольника. Зная, что сумма углов в треугольнике составляет 180°, составим и решим уравнение:
(x + 60°) + x + x = 180°
Значит, 

Задача 157.
треугольник ΔABC – прямоугольный
c = 26 см – гипотенуза
Найти: больший катет b
Пусть x – коэффициент пропорциональности. По теореме Пифагора составим и решим уравнение:
(5x) 2 + (12x) 2 = 26 2
25x 2 + 144x 2 = 676
b = 12 • 2 = 24 (см)
Задача 158.


c = 13 – гипотенуза
По теореме Пифагора получаем:
a = 
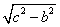

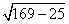

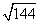
Тогда площадь треугольника
SΔABC = 


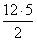
= 30 (квадратных единиц)
Задача 159.
треугольник ΔABC – равнобедренный,


c = 4 
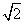
Найти: площадь треугольника SΔABC = ?
SΔABC = 

Т.к. Δ ABC – равнобедренный, то углы при основании по 45° и катеты равны a = b.
По теореме Пифагора получаем:
Тогда (4 
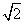
Тогда площадь треугольника
SΔABC = 


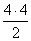
= 8 (квадратных единиц)
Задача 160.




Найти: радиус описанной окружности R = ?
Т.к. AH – медиана, то CH = 

По теореме Пифагора получаем:
Тогда CH = 


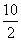
Точка H – центр описанной окружности
Т.к. R = AH, то R = AH = CH = 5 ед.
Задача 161.


соотношение острых углов




AC = 4 
Найти: радиус описанной окружности R = ?


Тогда 



Следовательно, BC = 

По теореме Пифагора получаем:
AC 2 + 
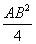
AC 2 = 

AB 2 = 
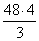
R = AD = BD = 8 : 2 = 4 (ед)
Задача 162.




радиус описанной окружности
Тогда AB = 2,5 • 2 = 5
По теореме Пифагора получаем:
AC = 
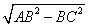

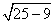

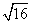




tg 


0,6 = 
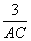

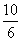
Задача 164.


Найти: 



Т.к. AH = AC, то Δ AHC – равнобедренный.
Точка H – радиус вписанной окружности, поэтому AH = CH, но AH = AC, следовательно, AH = CH = AC.
Тогда Δ AHC – равносторонний.
Значит, 





Задача 165.
треугольник Δ ABC – правильный, равносторонний,
SΔABC = 
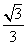
Найти: длину биссектрисы BH = ?


Рассмотрим Δ ABC – равнобедренный, где




Тогда BH – медиана, высота.
Значит, перпендикулярны отрезки BH 
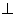
Рассмотрим треугольники Δ ABH и Δ BHC.
AB = BC, по условию.
AH = CH, BH – медиана.
Значит, треугольники равны Δ ABH = Δ BHC.
Т.е. SΔABH = 




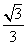

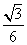
SΔABH = 

Рассмотрим треугольник Δ ABH.
Т.к. BH – биссектриса, то угол 

AH = 

SΔABH = 


AB • BH = 

По теореме Пифагора получаем:
AB 2 = AH 2 + BH 2
AB 2 = 

BH 2 = 

BH = 
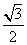
Используя результат (**) в уравнении (*), получаем
AB • 
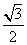

AB 2 = 
AB = 
Тогда AB • BH = 






Задача 166.
треугольник Δ ABC – правильный, равносторонний,


R = 
Найти: площадь треугольника
Рассмотрим Δ ABO (AO = BO = R) 

Проведем из вершины O к AB высоту OH.
Рассмотрим Δ AOH, где 

Т.к. 







OH = 


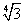

По теореме Пифагора получаем:
OH 2 + AH 2 = OA 2

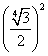

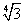



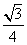
= 
AH 2 = 
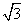

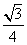

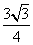



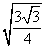

Тогда площадь треугольника
SΔAOH = 




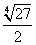

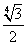

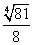

Следовательно, SΔABO = 2 • SΔAOH = 2 • 
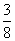


Тогда площадь треугольника
SΔABC = 3 • SΔABO = 3 • 


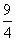




Площадь ромба SABCD = 384
Соотношение диагоналей ромба:
Найти: сторону ромба AB = ?
SABCD = 

Пусть x – коэффициент пропорциональности. Тогда
SABCD = 

Следовательно, диагональ BD = 4x = 4 • 8 = 32
AC = 3x = 3 • 8 = 24
Поэтому половина диагонали AO = 



BO = 



По теореме Пифагора получаем:
AO 2 + BO 2 = AB 2
Сторона ромба AB = 
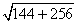

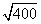
Задача 168.
треугольник Δ ABD – равнобедренный,


Найти: площадь треугольника
SΔABD = 

Проведем высоту BH к основанию AD.
По свойству равнобедренного треугольника:
BH – медиана, биссектриса, высота.
Т.к. BH – медиана, то AH = DH = 16 : 2 = 8 (ед.)
Рассмотрим треугольник Δ ABH, где угол 

По теореме Пифагора получаем:
AB 2 = AH 2 + BH 2
BH = 
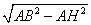

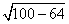

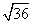
Тогда площадь треугольника
SΔABD = 



Ответ: площадь треугольника SΔABD = 48 кв.ед.

Задача 169.
треугольник Δ ABC –равнобедренный,
основание AC больше высоты BH на 15: AC > BH на 15
Найти: основание AC = ?
Т.к. треугольник Δ ABC –равнобедренный, то BH – высота, медиана, биссектриса.
Тогда AC = AH + CH = AH + AH = 2 AH
Рассмотрим Δ ABH – прямоугольный.
Пусть AC = (x) ед. 


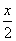
Тогда AB = (x – 15) ед. (по условию).
По теореме Пифагора решим уравнение:
(x – 15) 2 = ( 
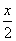



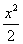
4 (x 2 – 30x) = x 2
4x 2 – 120x = x 2
3x 2 – 120x = 0 | : x
Таким образом, 40 ед. – длина основания.
Ответ: AC = 40 ед.
Видео:Параллельный перенос. Симметрия. Поворот | МатематикаСкачать

Подобные треугольники
Задача 170.






CH – биссектриса угла 

Доказать: подобие треугольников
Δ BHC 









Т.к. CH – биссектриса угла 





Рассмотрим Δ BHC








Тогда 



Поэтому треугольники подобны Δ BHC 



верхнее основание BC = 4 см
нижнее основание AD = 10 см
диагональ BD = 8 см
часть диагонали BO = ?
соотношение периметров треугольников


Углы равны 



Углы равны 



Тогда треугольники подобны Δ BCO 




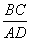

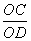







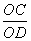













Пусть BO = x, AO = 8 – x. Тогда 10x = 4 • (8 – x)
x = 2 

Следовательно, BO = 2 



Ответ: BO = 2 



Задача 172.
ΔABC 



P (ΔABC) = 12 +16 + 20 = 48 (дм)
Т.к. треугольники подобны, то

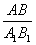

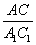




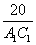


Тогда соотношение периметров треугольников

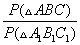
Из равенств (*) и (**) следует



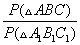




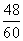

B1C1 = 
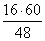
Тогда 





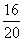



A1B1 = 
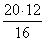
Задача 173.


стороны трапеции пересекаются в точке M:
Рассмотрим треугольники ΔAMD и ΔBMC:








Тогда, по первому признаку подобия треугольников:
треугольники подобны Δ AMD 


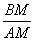

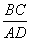

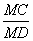


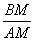

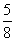
но AM = AB + BM = 3,9 + BM
8 • BM = 5 (3,9 + BM)

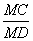

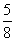
Видео:Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

Урок по теме «Решение задач по теме «Движение»
Разделы: Математика
Образовательная: совершенствовать знания учащихся по теме “Движение”, Показать применение преобразования “Движения” при решении геометрических и практических задач.
Развивающая: развитие умения обобщать, развитие интереса к изучаемому предмету.
Воспитательная: выработать внимание, самостоятельность при работе на уроке.
I. Орг.момент
II. Проверка домашней работы
III. Устная работа
1) Вспомнить определение преобразования движения.
2) Виды движений. К доске вызываются 4 ученика, каждый из них формулирует определение конкретного вида преобразования Движения. На доске чертится следующий кластер:
3) Повторить свойства движений.
IV. Решение задач
Задача № 1. По одну сторону от отрезка АЕ построены равносторонние треугольники АВС и СДЕ; Р – середина ВЕ, М – середина АД. Докажите, что треугольник СМР – равносторонний.
Выполним преобразование поворот вокруг точки С на угол 60 0 против часовой стрелки. Точка Е переходит в точку D, точка В – в точку А.Отрезок ВЕ переходит в отрезок DА. По свойству поворота середина ВЕ переходит в середину DА, т.е. точка Р переходит в точку М. Значит СР=СМ, и угол РСМ=60 0 . Следовательно, треугольник СМР равносторонний.
Задача № 2 Построить равносторонний треугольник АВС с вершинами на трех данных параллельных прямых.
Допустим, что треугольник построен. Тогда, при повороте вокруг точки А против часовой стрелки на угол 60 0 точка С переходит в точку В, а прямая m3 в прямую m.
Построение:
- На прямой m1 взять точку А.
- Повернуть прямую m3 вокруг точки А против часовой стрелке на угол 60 0 . Прямая m3 переходит в прямую m . Точка пересечения этих прямых есть точка В.
- Выполнить поворот вокруг точки А на угол 60 0 по часовой стрелке точку В. Полученная точка и есть точка С.
- Построить треугольник АВС.
Задача № 3 Два прямоугольных треугольника расположены так, что их медианы проведенные к гипотенузе параллельны и равны. Докажите, что угол между некоторыми катетами вдвое меньше угла между гипотенузами.
Выполним параллельный перенос на вектор 
Построим окружность с центром в точке М1 и радиуса М1А. М1 – середина гипотенузы прямоугольных треугольников® точки А, А1, С1, В1, В – лежат на этой окружности. Угол между гипотенузами АМ1А1 – центральный угол, опирающийся на дугу АА1, угол между катетами АС1А1 – также опирается на эту дугу и он вписанный. По теореме о вписанном угле 2? АС1А1=? АМ1А1
Задача № 4 (Задача на применение движения (параллельного переноса, неравенство треугольника) В каком месте следует построить мост MN через реку, разделяющую две данные деревни А и В, чтобы путь АМNВ из деревни А в деревню В был кратчайшим? (берега реки считаются параллельными прямыми, мост строиться перпендикулярно реке).
Предположим, что некоторое положение моста найдено. При параллельном переносе, переводящем точку М в точку N, точка А перейдет в некоторую точку А1. Тогда АМ+МN+NВ=АА1+А1N+NB
Отсюда вытекает следующий способ построения . Выполним параллельный перенос точки А на вектор 
V. Подведение итогов урока
1. Вопросы на стр. 281.
2. №1176, Дополнительная задача.
Дополнительная задача: На сторонах треугольника АВС построены из вне равносторонние треугольники АВС1, ВСА1, АСВ1. Докажите, что АА1, ВВ1, СС1 равны и угол между любыми двумя отрезками равен 60 0 .
Выполним преобразование поворот вокруг точки А по часовой стрелке на угол равный 60 0 . При этом АС1® АВ, а АС® АВ1. Следовательно СС1® В1В. Следовательно, отрезки СС1 и В1В равны и угол между ними 60 0 , т.к. поворот сохраняет равенство углов.
Аналогично для сторон АА1 и СС1.
Литература
- Геометрия: Учеб для 7-9 кл. образовательных . учреждений/ Л.С.Атанасян, В.Ф.Бутузов, и др.
- Геометрия 7-9, Гордин Р.К. Сборник задач
🎬 Видео
Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Параллельные прямые | Математика | TutorOnlineСкачать

Геометрия 9 класс (Урок№30 - Поворот.)Скачать

Геометрия 9 класс : Параллельный перенос и поворотСкачать

6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

#192 ПОВОРОТ И ПЕРЕНОС // ТРЕУГОЛЬНИКСкачать

Перенос треугольника по векторуСкачать
Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

ЕГЭ: задача 14. Параллельный перенос.Скачать
Нахождение истинной формы плоской фигуры методом плоско параллельного перемещенияСкачать