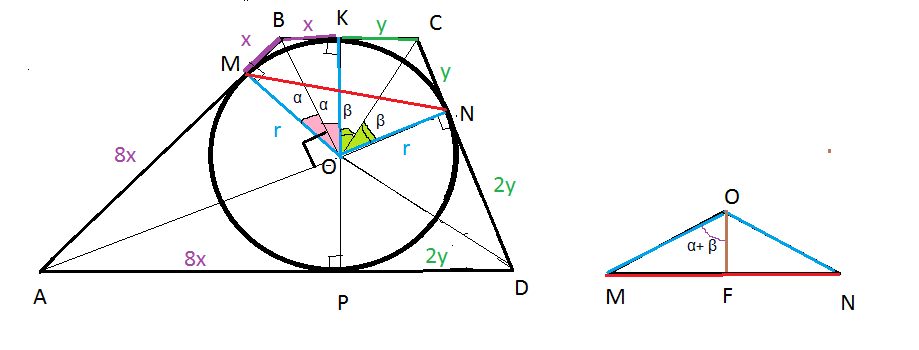
Окружность, вписанная в трапецию ABCD, касается ее боковых сторон AB и CD в точках M и N соответственно. Известно, что AM = 8MB и DN = 2CN.
а) Докажите, что AD = 4BC.
б) Найдите длину отрезка MN, если радиус окружности равен
а) Пусть окружность касается оснований BC и AD в точках K и L соответственно, а ее центр находится в точке O.
Лучи AO и BO являются биссектрисами углов BAD и ABC соответственно, поэтому
то есть треугольник AOB прямоугольный. Аналогично, треугольник COD тоже прямоугольный. Пусть BM = x, CN = y, тогда AM = 8x, DN = 2y.
б) Заметим, что поэтому
Пусть прямые AB и CD пересекаются в точке P, а прямые MN и PO пересекаются в точке Q. Тогда треугольники BPC и APD подобны, поэтому AP = 4BP, AB = 3BP, BP = 3x, PN = PM = 4x. Прямая PO является серединным перпендикуляром к MN. В прямоугольном треугольнике OMP получаем:
Значит,
Приведем другое решение пункта а)
Пусть окружность касается оснований BC и AD в точках K и L соответственно, ее центр находится в точке O, а BM = x, CN = y, тогда AM = 8x, DN = 2y. Поскольку точки M, K, N и L — точки касания,
и
Опустим высоты BH и CQ:
тогда по теореме Пифагора
Поскольку
имеем
откуда
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Содержание
Видео:Трапеция и вписанная окружностьСкачать  Задача 16865 Окружность, вписанная в трапецию ABCD.УсловиеОкружность, вписанная в трапецию ABCD, касается ее боковых сторон АВ и CD в точках М и N соответственно. Известно, что АМ=8МВ и DN=2CN. а) Докажите, что AD=4BC. б) Найдите длину отрезка MN, если радиус окружности равен sqrt(6) Решениеа) Сумма углов трапеции, прилежащих к боковой стороне, равна 180 градусов. AD=AP+DP=8x+2y=8x+2*2x=12x б) sin( альфа + бета )= Треугольник MON — равнобедренный, О т в е т. MN=4 Видео:Окружность, вписанная в трапециюСкачать  Окружность, вписанная в трапецию ABCD, касается ее боковых сторон AB и CD в точках M и N соответственно?Геометрия | 5 — 9 классы Окружность, вписанная в трапецию ABCD, касается ее боковых сторон AB и CD в точках M и N соответственно. Известно, что AM = 8MB и DN = 2CN. Докажите, что AD = 4BC. А) Пусть окружность касается основанийBCиADв точкахKиLсоответственно, а ее центр находится в точкеO. ЛучиAOиBOявляются биссектрисами угловBADиABCсоответственно, поэтому. Так как касательные к окружности из одной точки равны, то : BC + AD = 9MB + 3CN. AD = 6MB + 3BC — BC или AD = 8MB + 2CN = 6MB + 2BC. Треугольники АВО и СОD — прямоугольные (так как боковая сторона трапеции видна из центра вписанной в нее окружности под углом 90° — свойство). Высоты ОМ и ОN (равные радиусу) равны. По свойству высоты из прямого угла имеем : ОМ = (2√2) * МВ ; ОN = √2 * CN. Тогда 6МВ = 2МВ + 4МВ = 2МВ + 2CN = 2ВС. AD = 6MB + 2BC (доказано выше). AD = 2BC + 2BC = = 4ВС, что и требовалось доказать. Видео:В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. окружность проходит через точки C,DСкачать  В трапецию вписана окружность?В трапецию вписана окружность. Найти периметр трапеции если ее боковые стороны равны 7см и 9см. Видео:Геометрия В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит черезСкачать  Точка E середина боковой стороны CDMA трапеции ABCD?Точка E середина боковой стороны CDMA трапеции ABCD. Докажите что площадь треугольника ABE равна половине площади трапеции. Видео:Все виды №25 из банка ФИПИ ОГЭ по математикеСкачать  45 баллов?Основания AD и BC трапеции ABCD и боковая сторона AB равны соответственно 21, 7 и 12. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если сумма углов при основании трапеции равна 90 градусов. Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать  В трапеции АВСД углы при вершинах А и В прямые, а боковая сторона СД ровно вдвое длинее меньшего основания ВС?В трапеции АВСД углы при вершинах А и В прямые, а боковая сторона СД ровно вдвое длинее меньшего основания ВС. Известно, что в эту трапецию можно вписать окружность. Построена окружность, которая касается большего основания АД, боковой стороны СД и вписанной окружности трапеции. А) Прямая, проходящая через центр построенной окружности и центр окружности, вписанной в трапецию, пересекает сторону АВ в точке Р. Докажите, что АР / ВР = АД / ВС. Б) Найти радиус плстроенной окружности, если радиус вписанрой в трапецию окружности равен 1. Видео:Задача про трапецию, описанную около окружностиСкачать  Боковая сторона равнобедренного треугольника равна 18, основание равно 12?Боковая сторона равнобедренного треугольника равна 18, основание равно 12. Вписанная окружность касается боковых сторон в точках С и Е. Видео:ОГЭ по математике, задание 26, тренировочный вариант 1Скачать  Боковая сторона равнобедренного треугольника равна 18, основание равно 12?Боковая сторона равнобедренного треугольника равна 18, основание равно 12. Вписанная окружность касается боковых сторон в точках С и Е. Видео:№692. В треугольник ABC вписана окружность, которая касается сторон АВ, ВС и СА в точках Р, Q и RСкачать  В трапеции ABCD основания AD и BC равны соответственно 5 и 2?В трапеции ABCD основания AD и BC равны соответственно 5 и 2. Окружность, описанная около треугольника ABC, касается основания AD и боковой стороны CD. Найти радиус окружности. Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать  Большая боковая сторона прямоугольной трапеции равна 12корень из 2см, а острый угол — 45°?Большая боковая сторона прямоугольной трапеции равна 12корень из 2см, а острый угол — 45°. Найдите площадь трапеции, если известно, что в нее можно вписать окружность. Видео:✓ Как решить трапецию | ЕГЭ-2020. Задание 16. Профильный уровень. Основная волна | Борис ТрушинСкачать  Большая боковая сторона прямоугольной трапеции равна 12√2см, а острый угол — 45°?Большая боковая сторона прямоугольной трапеции равна 12√2см, а острый угол — 45°. Найдите площадь трапеции, если известно, что в нее можно ВПИСАТЬ окружность. Видео:Трапеция и окружность. 9 классСкачать  В трапецию абсд вписана окружность с центром и?В трапецию абсд вписана окружность с центром и. Найдите периметр трапеции если сумма растояний от точки и до середин боковых сторон равна 30. Видео:14.43.1. Планиметрия. Гордин Р.К.Скачать  В трапецию вписана окружность, точка касания окружности с боковой стороной делит эту сторону на два отрезка — 8 и 2?В трапецию вписана окружность, точка касания окружности с боковой стороной делит эту сторону на два отрезка — 8 и 2. Найти высоту трапеции. Вы зашли на страницу вопроса Окружность, вписанная в трапецию ABCD, касается ее боковых сторон AB и CD в точках M и N соответственно?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке. 1) 30, 30, 150, 150 градусов 2) 77, 77, 123, 123 градусов. 1)угол B : 180 — (90 + 60) = 30 градусов. 2) катет АСлежит против угла в 30 градусов, значит равен половине гипотенузы АВ — — — > значит АВ = 6 3) катет СВ (по пифагору). 1. Секущая — это прямая, которая пересекает кривую в двух точках или прямая, которая пересекает две другие прямые. 2. Нет, не всегда. Чтобы треугольник существовал, сумма двух каждых сторон должна быть больше третьей стороны. 2) рассмотрим труг — к BCD, BM = MC, CN = ND поэтому MNсредняя линия труг — ка BCD, поэтому MN II BD, т. Е. колинеарны, я канеш не математик, но эт решить могу. Ответ : Объяснение : 1. Провести линию и построить к ней два перпендикуляра на расстоянии длины, отложить на них ширину и соединить . (перпендикуляр строится циркулем : от точки на прямой отложить два равных отрезка из ник построить окруж радиус вз.. Я позволю себе выложить здесь оформленное решение задачи, которое дано в комментариях. Данное решение, на мой взгляд, заслуживает большего предпочтения. По свойству биссектрисы треугольника CD : CE = DF : FE = 2 : 1 ⇒ CE = 2CD CG — биссектриса ΔCHE и по тому же свойству CH : CE = HG : GE = 4 : 5 Получаем систему CH : CE = HG : GE = 4 : 5 CE = 2CD (CD + 3 / 2) : CE = 4 : 5 CE = 2CD 4CE = 5CD + 15 / 2 .. 2 + 4 = 6 сумма всех величин 90÷6 = 15 градусы на одну величину 2×15 = 30° первый угол 4×15 = 60° второй угол. А вот насчёт второй задачи есть вопросы? Там найти углов или сравнить т. К накрестлежащие , соответственные и вертикальные. Х + х + 5 = 50 2х + 5 = 50 2х = 50 — 5 = 45 х = 45 : 2. 💥 ВидеоОГЭ. Математика. Задание 26 | Прямоугольная трапеция и окружность | Борис Трушин |Скачать  Планиметрия с окружностями | Задачи из ЕГЭ прошлых лет | №17 ЕГЭ по математикеСкачать  Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать  Вписанные и описанные окружности. Вебинар | МатематикаСкачать  ОГЭ Задание 25 Демонстрационный вариант 2022, математикаСкачать  Радиус описанной окружности трапецииСкачать  Окружность, вписанная в трапецию.A circle inscribed in a trapezoid.Скачать  |