Задача 302 тип треугольника (6 видео) | Курс школьной геометрии

Задача «Треугольник»

Заданы длины трех отрезков a, b, c. Необходимо определить, можно ли из них составить треугольник. В случае утвердительного ответа определить его тип: остроугольный, прямоугольный или тупоугольный.

Вход. Три целых числа a, b, c – длины трех отрезков.

Выход. Строка, содержащая информацию о треугольнике: “ACUTE”, если он остроугольный, “RIGHT” если прямоугольный и “OBTUSE” если тупоугольный. Если из трех отрезков составить треугольник нельзя, то вывести “NONE”.

Из трех отрезков a, b, c можно составить треугольник, если выполняется неравенство треугольника: сумма длин двух любых сторон треугольника строго больше длины третьей.

Из теоремы Пифагора следует, что треугольник со сторонами a, b, c является прямоугольным, если выполняется одно из следующих равенств:

a 2 = b 2 + c 2 или b 2 = a 2 + c 2 или c 2 = a 2 + b 2

Треугольник будет остроугольным, если квадрат каждой стороны строго меньше суммы квадратов двух других сторон. То есть одновременно выполняется три неравенства:

a 2 b 2 + c 2 , b 2 a 2 + c 2 , c 2 a 2 + b 2

Треугольник является тупоугольным, если существует такая сторона, квадрат которой строго больше суммы квадратов двух других сторон. То есть выполняется одно из трех неравенств:

a 2 > b 2 + c 2 или b 2 > a 2 + c 2 или c 2 > a 2 + b 2

Условие тупоугольности можно не проверять: если треугольник не является ни остроугольным, ни прямоугольным, то он является тупоугольным. Для вывода результата воспользуемся типом string .

if ((a >= b + c) or (b >= a + c) or (c >= a + b))

then res := ‘NONE’ else

if ((a*a = b*b + c*c) or (b*b = a*a + c*c) or (c*c = a*a + b*b))

then res := ‘RIGHT’ else

then res := ‘ACUTE’ else

Задача решена, но имеет один недостаток. При проверке типа треугольника приходится каждый раз проверять три условия: в каждом из условных операторов if стоит три выражения. Можно сделать так, что в каждом условном операторе будет стоять лишь одно условие. Подумайте, как это сделать?

Ответ на вопрос дает сортировка. Отсортируем по возрастанию длины исходных отрезков. Пусть у нас далее имеют место неравенства: a £ b £ c. Тогда для проверки неравенства треугольника достаточно проверить лишь a + b > c, так как оба других неравенства b + c > a и a + c > b выполняются. Для проверки прямоугольности достаточно проверить только равенство c 2 = a 2 + b 2 , так как при a £ b £ c гипотенузой может быть только сторона c. В случае тупоугольности наибольшей стороной может быть только c, поэтому для существования тупого угла в треугольнике достаточно выполнение условия c 2 > a 2 + b 2 . Треугольник будет остроугольным, если c 2 a 2 + b 2 .

Например, в языке Си, отсортировать три числа можно так:

Язык Паскаль вообще не имеет функций сортировки. Здесь, уже на элементарной задаче, мы столкнулись с бедностью языка Паскаль. Реализовать сортировку непосредственно операциями сравнения в этой задаче можно, так как число переменных не велико. Если бы их было больше – требовалось бы заводить массив и уже писать один из классических алгоритмов сортировки.

Если мы сможем эффективно отсортировать числа a, b, c, то программа примет вид:

if c >= a + b then res := ‘NONE’ else

if c*c = a*a + b*b then res := ‘RIGHT’ else

Содержание

Часть 2: Тестирование простого приложения (Тестирование ПО)
Записная книжка рассеянного [в пространстве и времени] программиста
Часть 2: Тестирование простого приложения (Тестирование ПО)
Оглавление
Первое приложение
Тестируем
Литература
Исходные тексты программ
Оглавление
Как определить вид треугольника
🎥 Видео

Видео:ПРОБЛЕМНЫЕ ЗАДАЧИ #1 ЕГЭ 2024 с Высотой в Прямоугольном ТреугольникеСкачать

Часть 2: Тестирование простого приложения (Тестирование ПО)

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Записная книжка рассеянного [в пространстве и времени] программиста

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Часть 2: Тестирование простого приложения (Тестирование ПО)

Видео:Теорема Пифагора. 8 КЛАСС | Математика | TutorOnlineСкачать

Первое приложение

Программа считывает три целочисленных значения из консоли. Эти значения интерпретируются как длины сторон треугольника. Программа выводит сообщение о том, каким является данный треугольник — разносторонним, равнобедренным или равносторонним.

Напишем, функцию, которая принимает на вход три стороны треугольника, которые заданы целыми числами и возвращает тип треугольника. Сохраним написанный код в файле triangle.php.

Функция достаточно тривиальна, поэтому мы не будем останавливаться на ее реализации. Нас будет интересовать, как найти в ней ошибки.

Для начала потребуется реализовать механизм, который позволит вводить данные с консоли и получать результат. Сохраним следующий код в файле main.php. Чуть позже вы поймете, почему мы используем разные файлы для самой функции и для кода, который обрабатывает пользовательский ввод.

Код также достаточно тривиален. Теперь мы можем запустить полученное приложение (да, это именно приложение — последовательность инструкций, определяющих процедуру решения конкретной задачи компьютером).

Откроем терминал, перейдем в каталог, с проектом и выполним следующую команду (для того, чтобы все сработало у вас должен быть установлен интерпретатор php в системе).

Программа будет ожидать ввод трех чисел, разделенных пробелами.

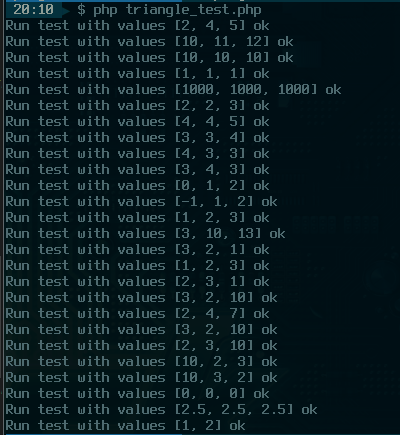
И вот что мы можем увидеть на экране.

Поэкспериментируйте немного с программой вводя разные наборы чисел.

А теперь рассмотрим эту программу с точки зрения разработчика, которому досталось ее тестировать. Какие наборы тестов он должен разработать, чтобы отыскать все возможные баги? Прежде чем читать дальше подумайте и попробуйте посчитать то количество, которое придумали вы.

Итак. Ниже приведен набор тестовых сценариев, которые должны быть написаны для нашей функции.

тест для проверки действительно неравностороннего треугольника (наборы [1, 2, 3], [2, 5, 10] треугольниками не являются).
проверка на действительно равносторонний треугольник
проверка на равнобедренный треугольник (наборы вида [2, 2, 4] треугольником не являются)
как минимум три теста для проверки равнобедренного треугольника, которые представляют собой перестановки одного и того же набора чисел ([3, 3, 4], [3, 4, 3], [4, 3, 3])
тест на нулевую длину одной из сторон
тест на сторону, имеющую длину меньше нуля
проверка набора чисел, в котором сумма длин двух сторон равна третьей
тест перестановок для троек чисел из теста 7
проверка набора чисел, в котором сумма длин двух сторон меньше третьей ([12, 15, 30])
тест перестановок для троек чисел из теста 9
проверка на нулевую длину всех трех сторон
проверка на передачу нецелочисленных значений
проверка на передачу неполного набора значений
проверка не только входных данных, но и ожидаемого выходного значения в каждом из тестов 1-13

Если вы не смогли назвать все кейсы, то не пугайтесь. Среднее число тестов, которые называли в разное время опытные разработчики составило 7,8.

Конечно нет никаких гарантий того, что набор тестов, удовлетворяющих перечисленным условиям, обнаружит все возможные ошибки. Но поскольку случаи 1-13 представляют ошибки, реально встречающиеся в различных версиях данной программы, адекватное тестирование должно обнаружить хотя бы их.

Это упражнение должно было продемонстрировать вам, что тестирование простых программ наподобие вышеприведенной является отнюдь не тривиальной задачей. А теперь попытайтесь представить себе, насколько трудоемким окажется тестирование, скажем, бухгалтерской программы крупного предприятия, компилятора или же системы управления воздушным движением, объем кода которых может достигать сотен тысяч строк. Еще большие трудности возникают с приложениями, которые написаны с использованием объектно-ориентированных языков (куда входит и php) и подходов. В частности, тесты для подобных приложений должны выявлять ошибки с созданием экземпляров объектов и взаимодействия между ними.

Однако, какой бы устрашающей ни казалась задача, адекватное (достаточно полное) тестирование программ является ключевой и, как вы убедитесь далее, вполне реализуемой частью процесса разработки программного обеспечения.

Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Тестируем

Конечно же самым простым решением будет просто закодировать все тестовые случаи для нашего проекта и написать нечто вроде следующего кода (файл triangle_test_simple.php).

И такое часто практикуется. Особенно в среде разработчиков на CC++. На каждый логически связанный набор тестовых случаев создается свой файл. Который содержит множество функций обрабатывающих по одному сценарию каждая.

В этом нет ничего плохого. Единственный минус такого подхода — отсутствие готового инструментария, который реализует все необходимые операции по обслуживанию и запуску тестов. Весь инструментарий приходится для каждого проекта реализовывать заново. Либо изготавливать свою собственную обвязку, которая будет кочевать из проекта в проект.

Один из вариантов создания инструмента для работы с подобными тестами вы можете увидеть в файле triangle_test.php. Запустите его и увидите на экране подробный лог тестирования проекта.

Видео:Геометрическое решение задачи из видео Бориса Трушина. Изогональное сопряжение.Педальный треугольникСкачать

Литература

Видео:Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

Исходные тексты программ

Видео:Треугольники. 7 класс.Скачать

Как определить вид треугольника

Онлайн калькулятор поможет узнать по сторонам, является ли треугольник прямоугольным, равнобедренным, равносторонним или разносторонним.

Как определить, что треугольник прямоугольный: по Теорема Пифагора — сумма квадратов длин катетов равна квадрату длины гипотенузы c 2 = a 2 + b 2
Как определить, что треугольник равнобедренный: один из признаков равнобедренного треугольника — две стороны равны.
Как определить, что треугольник равносторонний: все стороны равны.

Принято выделять три типа треугольников:
тупоугольные — один из углов более 90 градусов,
прямоугольные — один из угол равен 90 градусов,
остроугольные — все углы менее 90 градусов.
Это классификация по типу углов.