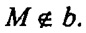B параллельна bc прямая a не принадлежит плоскости abc доказать прямые a и b скрещивающиеся (6 видео)

Докажите, что b и с — скрещивающиеся прямые. Вопросы и задачи 36, Геометрия, 10-11 класс, Атанасян Л.С.

Здарово. Поможете решить?

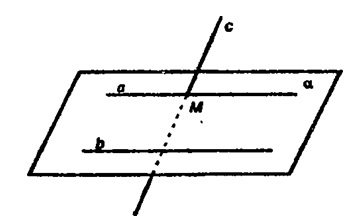
Прямая с пересекает прямую а и не пересекает прямую b, параллельную прямой а. Докажите, что b и с — скрещивающиеся прямые.

Могу помочь, если актуально еще

Т.к. а || b, то существует пл. α, что
Пусть с пересекает а в т. М. а || b, значит,
По признаку скрещивающихся прямых, с и b скрещиваются.

Содержание

скрещивающиеся прямые план-конспект
Скачать:
Предварительный просмотр:
Скрещивающиеся прямые. Проведение через одну из скрещивающихся прямых плоскости, параллельной другой прямой
🔍 Видео

Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

скрещивающиеся прямые
план-конспект

Для учащихся старшего звена (программа «Геометрия вокруг нас») предлагается вспомнить основные теоремы по теме «Скрещивающиеся прямые». Даны задачи как для самостоятельного решения, так и разобранные, которые послужат пощниками в самостоятельной работе.

Видео:№39. Докажите, что если АВ и CD скрещивающиеся прямые, то AD и ВС также скрещивающиеся прямые.Скачать

Скачать:

Вложение	Размер
skreshchivayushchiesya_pryamye.docx	399.91 КБ

Бесплатный марафон подготовки к ЕГЭ на зимних каникулах

Учи.Дома запускает бесплатный марафон в котором каждый день. В течении 5 дней утром ты будешь получать одно задание по выбранному предмету, а вечером его решение. Твоя задача, успеть выполнение задание до того как получишь ответ.

Бесплатно, онлайн, подготовка к ЕГЭ

Видео:№36. Прямая с пересекает прямую а и не пересекает прямую b, параллельную прямой а.Скачать

Предварительный просмотр:

Две прямые в пространстве называются скрещивающимися , если они не пересекаются и не параллельны.

Теорема ( признак скрещивающихся прямых ). Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

Доказательство . Пусть прямая а лежит в плоскости α, а прямая b пересекает эту плоскость в точке В, не лежащей на прямой а.

Докажем, что прямые а и b скрещивающиеся, т.е. не существует плоскости, в которой они обе лежат. Предположим, что прямые а и b лежат в некоторой плоскости β. Тогда плоскость β проходит через прямую а и точку В, а следовательно, совпадает с плоскостью α (так как через прямую и не лежащую на ней точку проходит единственная плоскость).

Получили, что прямая b лежит в плоскости α, а это противоречит условию теоремы. Таким образом, наше предположение неверно, а значит, прямые а и b – скрещивающиеся.

Теорема . Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная второй прямой, и притом только одна.

Доказательство . Пусть а и b – скрещивающиеся прямые. Докажем, что через прямую b проходит плоскость, параллельная прямой а.

Через какую-либо точку B прямой b проведем прямую с, параллельную прямой а.

Пусть α – плоскость, проходящая через прямые b и с. Так как прямая а не лежит в плоскости α и параллельная прямой с, лежащей в этой плоскости, то прямая параллельная плоскости α.

Плоскость α – единственная плоскость, проходящая через прямую b и параллельная прямой а.

Действительно, любая другая плоскость, проходящая через прямую b, пересекается с прямой с, а, следовательно, пересекается и с параллельной ей прямой.

Пример 1 . Используя рисунок, укажите прямую, скрещивающуюся с прямой АВ и принадлежащую плоскости АВВ 1 .

Решение . Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

Прямая АВ лежит в плоскости АВВ 1 . Эту плоскость пересекает прямая А 1 С 1 , следовательно, прямые АВ и А 1 С 1 скрещиваются.

Ответ : АВ и А 1 С 1

Задание 1 . Используя рисунок, укажите прямую, скрещивающуюся с…

прямой В 1 D 1 и принадлежащую плоскости АВС

прямой СD 1 и принадлежащую плоскости АВВ 1

прямой А 1 D и принадлежащую плоскости ВСС 1

прямой СВ и принадлежащую плоскости АDD 1

Пример 2 . Сколько прямых, содержащих ребра треугольной призмы ABCA 1 B 1 C 1 скрещиваются с прямой ВС ?

Решение . Прямая ВС лежит в плоскостях АВС и ВСС 1 В 1 .

Эти плоскости пересекают прямые АА 1 , А 1 В 1 и А 1 С 1 . Следовательно, с прямой ВС скрещивается три прямых, содержащих ребра треугольной призмы.

Задание 2 . Сколько прямых, содержащих ребра…

куба ABCDA 1 B 1 C 1 D 1 скрещиваются с прямой АВ ?

правильной треугольной призмы АВСА 1 В 1 С 1 , скрещиваются с прямой АВ ?

треугольной пирамиды ТАВС ( Т – вершина пирамиды), скрещиваются с прямой АС ?

куба ABCDA 1 B 1 C 1 D 1 скрещиваются с прямой ВD 1 ?

правильной треугольной призмы ABCA 1 B 1 C 1 скрещиваются с прямой ВВ 1 ?

четырехугольной пирамиды ТАВСD ( Т – вершина пирамиды), скрещиваются с прямой ВС ?

правильной треугольной призмы ABCA 1 B 1 C 1 скрещиваются с прямой АВ 1 ?

четырехугольной пирамиды ТАВСD ( Т – вершина пирамиды), скрещиваются с прямой АС ?

прямоугольного параллелепипеда ABCDA 1 B 1 C 1 D 1 скрещиваются с прямой ВС ?

четырехугольной пирамиды ТАВСD ( Т – вершина пирамиды), скрещиваются с прямой ТС ?

Пример 3. DABC – треугольная пирамида. Точка Р лежит на ребре АС , а точка О – на медиане DF грани CDB . Верно ли, что прямые AD и РО параллельны?

Дано: DABC – пирамида.

Доказать: AD ║ PO

Предположим, что прямые AD и РО параллельны между собой, тогда они лежат в одной плоскости, т.е. точки А , Р , D и О лежат в одной плоскости.

Прямая DO пересекает плоскость АВС в точке F , не лежащей на прямой АР .

Следовательно, прямые DO и АР являются скрещивающимися, т.е. не существует плоскости, в которой лежат точки А , Р , D и О .

Это противоречит предположению параллельности прямых AD и РО , следовательно, прямые AD и РО не являются параллельными.

Задание 3 . Дан куб ABCDA 1 B 1 C 1 D 1 . Докажите, что данные прямые скрещиваются…

Задание 4 . Отметьте верные утверждения…

Через точку, не принадлежащую данной прямой, можно провести только одну прямую, параллельную этой прямой.

Через точку, не принадлежащую данной прямой, можно провести только одну прямую, перпендикулярную этой прямой.

Прямые, перпендикулярные одной и той же прямой параллельны.

Прямая, пересекающая одну из двух данных параллельных прямых, пересекает и другую.

Угол между скрещивающимися прямыми

Углом между скрещивающимися прямыми называется угол между пересекающимися параллельными им прямыми. Этот угол не зависит от того, какие взяты пересекающиеся прямые.

Для нахождения угла между двумя данными скрещивающимися прямыми а и b можно взять на одной из них, например на прямой а , некоторую точку О и провести через нее прямую b 1 , параллельную прямой b .

Тогда угол между прямыми а и b 1 будет равен углу между скрещивающимися прямыми a и b .

Пример 4 . Дана правильная треугольная призма АВСА 1 В 1 С 1 . Чему равен угол между прямыми АВ и А 1 С 1 ?

Дано: АВСА 1 В 1 С 1 – призма.

Найти: ∠ ( АВ;А 1 С 1 )

Прямые АВ и А 1 С 1 скрещиваются.

Углом между скрещивающимися прямыми называется угол между пересекающимися параллельными им прямыми.

Прямая А 1 С 1 || АС , АС пересекается с прямой АВ .

Поскольку призма АВСА 1 В 1 С 1 правильная, то в ее основании лежит равносторонний треугольник с углами в 60 О . Следовательно, прямыми АВ и А 1 С 1 равен 60 О .

Задание 3 . Чему равен угол между прямыми…

АВ и В 1 С 1 в кубе ABCDA 1 B 1 C 1 D 1 ?

СС 1 и АА 1 в прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 ?

АВ и В 1 С 1 в правильной треугольной призме ABCA 1 B 1 C 1 ?

АС и В 1 С 1 в кубе ABCDA 1 B 1 C 1 D 1 ?

АС и B 1 D 1 в прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 , если диагонали основания пересекаются под углом в 60 о ?

АВ и CС 1 в правильной треугольной призме ABCA 1 B 1 C 1 ?

АС и В 1 D 1 в кубе ABCDA 1 B 1 C 1 D 1 ?

АС и B 1 D 1 в прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 , если диагонали основания пересекаются под углом в 60 о ?

ВС и АА 1 в прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 ?

АА 1 и CС 1 в правильной треугольной призме ABCA 1 B 1 C 1 ?

Задание 4 . Решите задачу…

Прямые ОВ и CD параллельные, а ОА и CD – скрещивающиеся. Найдите угол между прямыми ОА и СD , если ∠ АОВ =40 О .

Прямые ОВ и CD параллельные, а ОА и CD – скрещивающиеся. Найдите угол между прямыми ОА и СD , если ∠ АОВ =135 О .

Найдите угол между скрещивающимися прямыми АВ и PQ , если точки Р и Q равноудалены от концов отрезка АВ .

Пример 6 . Длина ребра правильного тетраэдра равна 1. Найдите угол между прямыми и , где — середина ребра , — середина ребра .

Решение . Пусть прямая параллельная прямой и точка ее пересечения с . Тогда искомый угол между прямыми и равен углу . — средняя линия треугольника .

По теореме косинусов:

Поскольку и , получим , откуда .

Пример 7 . Сторона правильной треугольной призмы равна 8. Высота этой призмы равна 6. Найти угол между прямыми и .

Решение . Достроим треугольную прямую призму до четырехугольной прямой призмы, в основании которой ромб , составленный из двух равносторонних треугольников.

Полученная призма является прямым параллелепипедом. Поэтому . Значит, искомый угол . Площадь ромба равна произведению квадрата его стороны на синус угла: .

С другой стороны, площадь ромба можно найти как половину произведения длин его диагоналей: , следовательно, .

Из прямоугольного треугольника по теореме Пифагора находим . Аналогично, .

Из равнобедренного треугольника получаем .

Пример 8 . Точка — середина ребра куба . Найдите угол между прямыми и .

Решение . Примем ребро куба за единицу. Тогда .

Прямая , значит, искомый угол равен углу . Из прямоугольного треугольника с прямым углом имеем , тогда .

Пример 9 . На ребре куба отмечена точка так, что . Найдите угол между прямыми и .

Решение . Примем ребро куба за . Тогда .

Поскольку , получаем и .

Проведем через точку прямую, параллельную . Она пересекает ребро в точке , причем треугольники и равны. Искомый угол равен углу (или смежному с ним).

В прямоугольном треугольнике с прямым углом .

В треугольнике . Откуда . Тогда .

Пример 10 . Боковое ребро правильной треугольной пирамиды равно 10, а косинус угла при вершине боковой грани равен . Точка — середина ребра . Найдите косинус угла между прямыми и .

Решение . Пусть — середина .

Поскольку по теореме о средней линии треугольника, угол искомый. Найдём стороны треугольника .

По теореме о средней линии треугольника .

По теореме косинусов из треугольника получаем .

Чтобы найти , найдём сначала сторону основания по теореме косинусов из треугольника : . как высота в равностороннем треугольнике со стороной 8. Отсюда .

Пример 11 . – правильная треугольная призма, боковое ребро которой в два раза больше стороны основания. Точки и – середины ребер и . Вычислите косинус угла между прямыми и .

Решение . В плоскости грани строим прямую . Тогда угол между скрещивающимися прямыми и есть угол между пересекающимися прямыми и .

Пусть φ . В треугольнике по теореме косинусов , откуда .

В треугольнике ( , , ) . Отсюда .

Пример 12 . Все боковые грани призмы — квадраты. На ребрах , , и взяты соответственно точки , , и — середины этих ребер. Найдите угол между прямыми и .

Решение . Через прямую и точку , взятую на прямой , проведем плоскость, в результате чего получим сечение призмы — четырехугольник .

В плоскости через точку проведем прямую . Угол между прямыми и равен искомому углу.

На прямой возьмем точку , а на прямой — точку и найдем .

Пусть ребро призмы равно .

В прямоугольном треугольнике , . Тогда .

По теореме косинусов , откуда .

Таким образом, угол тупой, поэтому искомый угол , значит, , т.е. .

Пример 13 . В правильной шестиугольной пирамиде стороны основания равны 1, а боковые ребра равны 2, найдите косинус угла между прямыми и .

Решение . Прямая параллельна прямой . Следовательно, искомый угол — .

В равнобедренном треугольнике проведём медиану и высоту .

. Из прямоугольного треугольника получаем .

Пример 14 . В правильном тетраэдре найдите угол между высотой тетраэдра и медианой боковой грани .

Решение . Пусть и — средняя линия треугольника . Тогда , значит, и, следовательно, .

Кроме того, . Пусть длина ребра тетраэдра равна , тогда ; ; ; ; .

Пример 15 . Длины всех ребер правильной четырехугольной пирамиды равны между собой. Найдите угол между прямыми и , если отрезок — высота данной пирамиды, точка — середина ее бокового ребра .

Решение . Пусть отрезок — средняя линия треугольника ,параллельная его стороне .

Поскольку — правильная пирамида, точка — центр квадрата . Так как и , то , значит, . Прямые и параллельны, следовательно, угол между прямыми и равен углу между прямыми и , то есть острому углу прямоугольного треугольника .

Пусть длина ребра пирамиды равна , тогда ; ; и, следовательно, .

Пример 16 . В правильной треугольной призме все рёбра равны 1. Найдите косинус угла между прямыми и .

Решение . Поскольку , необходимо найти угол .

По теореме Пифагора . Тогда . Высота правильного треугольника равна . По теореме косинусов , откуда .

Пример 17 . В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 АВ=1 см, AD=2 см, АА 1 =1 см. Найдите угол между прямыми А 1 F и D 1 К, где точки F и К – середины ребер В 1 С 1 и AD соответственно.

Дано: ABCDA 1 B 1 C 1 D 1 – параллелепипед, АВ=1 см, AD=2 см, АА 1 =1 см.

Найти: ∠ (А 1 F, D 1 К)

Рассмотрим плоскость, проходящую через прямую A 1 F и точку К.

Плоскость проходит через прямую А 1 К, параллельную плоскости грани ВВ 1 С 1 С (так как А 1 К║В 1 О, где точка О – середина ребра ВС), а следовательно, пересекает эту грань по отрезку, параллельному прямой В 1 О, т.е. по отрезку FC.

Сечение параллелепипеда плоскостью есть четырехугольник КА 1 FC, который является параллелограммом (так как А 1 К=FC, А 1 К║FC). Следовательно, КС║A 1 F. Отсюда следует, что угол D 1 KC – искомый.

Градусную меру угла D 1 KC найдем из треугольника D 1 КС.

ΔKDD 1 =ΔCDD 1 , (DK=DC, ∠ KDD 1 = ∠ CDD 1 =90 o , DD 1 – общая сторона).

ΔKDC=ΔCDD 1 (DK=DD 1 , DC – общая сторона, ∠ KDC= ∠ CDD 1 =90 o ).

Отсюда следует, что треугольник D 1 KC – равносторонний. Значит, ∠ D 1 KC=60 о .

Пример 18 . SABC – тетраэдр. Точки F и К – середины его ребер АВ и АС соответственно. Найдите косинус угла между прямыми SF и ВК.

Дано: SABC – тетраэдр, AF=FB, AK=KC.

В плоскости SCF через точку О=ВК ∩ FC проведем прямую OD, параллельную прямой SF. Тогда угол DOK – искомый. Соединим точку D с точкой К и найдем косинус угла DOK треугольника DOK.

Для нахождения косинуса угла вычислим длины сторон треугольника DOK и воспользуемся теоремой косинусов.

Пусть длина ребра тетраэдра равна а, ∠ DOK=х.

В треугольнике DKC (CD= CS= a, CK= , ∠ KDC=60 o ) DK 2 =CK 2 +CD 2 -2CK ⋅ CDcos60 o , DK 2 = a 2 .

В треугольнике SFC OD║SF, OC= FC, следовательно, OD= SF= = . В треугольнике DOK (OD= , OK= BK= ) DK 2 =OD 2 +OK 2 -2OD ⋅ OKcosx, a 2 = a 2 + a2-2 cosx. Отсюда cosх=

Задание 5 . Решите задачу…

На ребрах AA 1 и CD куба ABCDA 1 B 1 C 1 D 1 взяты соответственно точки Р и Q — середины этих ребер. Найдите угол между прямой PQ и A 1 D.

На ребрах В 1 С 1 , АС и А 1 В 1 прямой призмы АВСА 1 В 1 С 1 , у которой АС=ВС=АА 1 и ∠ АСВ=90 о , взяты соответственно точки D и E – середины ребер В 1 С 1 и АС. Найти угол между прямой DE и АС 1 .

На ребрах B 1 C 1 , АС и А 1 В 1 прямой призмы АВСА 1 В 1 С 1 , у которой АС=ВС=АА 1 и ∠ АСВ=90°, взяты точки Р и Q — середины ребер АС и ВС. Найдите угол, который образует прямая АС 1 с прямой PQ.

В правильной призме ABCDA 1 B 1 C 1 D 1 угол между диагоналями BD 1 и B 1 D равен 90 о . Найти угол, который образует прямая B 1 D с прямой АА 1 .

Сторона основания правильной треугольной призмы равна 2 cм. Найдите косинус угла между прямыми, на которых лежат непересекающиеся диагонали двух смежных боковых граней призмы, если расстояния между этими прямыми равно 2 см.

В основании пирамиды SABCD лежит квадрат, а ее боковое ребро SA равно стороне основания и перпендикулярно плоскости основания. На ребре SD взяты точки М 1 , М 2 и М 3 – такие, что DM 1 =M 1 M 2 =M 2 M 3 =M 3 S. Найти угол, который образует прямая SD с прямой СМ 2 .

Основанием призмы АВСА 1 В 1 С 1 является прямоугольный треугольник АВС, у которого АС=ВС. Грань ВСС 1 В 1 перпендикулярна плоскости основания и угол С 1 СВ=45 о , а ВС 1 =ВС. Найти угол между прямой АС и А 1 В.

На ребрах В 1 С 1 , АС и А 1 В 1 прямой призмы АВСА 1 В 1 С 1 , у которой АС=ВС=АА 1 и угол АСВ=90 о , взяты соответственно точки D, E и F – середины ребер В 1 С 1 , АС и А 1 В. Найти угол между прямой DE и AF.

Основанием призмы АВСА 1 В 1 С 1 является прямоугольный треугольник, у которого АС=ВС. Грань ВСС 1 В 1 перпендикулярна плоскости основания, и ∠ С 1 CB=45°, а ВС 1 =ВС. Найдите угол, которые образует прямая АС 1 с прямой А 1 В.

На диагонали АС квадрата ABCD взяты точки К 1 , К 2 и К 3 – такие, что АК 1 =К 1 К 2 =К 2 К 3 =К 3 С. Квадрат ABCD согнут по диагонали АС так, что треугольник BK 2 D равносторонний. Найдите угол, который образует прямая CD с прямой ВК 1 .

Основанием призмы АВСА 1 В 1 С 1 является прямоугольный треугольник, у которого АС=ВС. Грань ВСС 1 В 1 перпендикулярна плоскости основания, и ∠ C 1 CB=45°, а ВС 1 =ВС. Найдите угол, который образует прямая АС 1 с прямой А 1 В.

В основании пирамиды SABCD лежит квадрат ABCD. Ребро SB перпендикулярно плоскости основания и SB:AB=1:1. На ребре SC взята точка Р – середина этого ребра. Найти угол, который образует прямая DP с прямой SA.

В основании пирамиды SABC лежит прямоугольный треугольник АВС ( ∠ С=90 о ). Ребро SС перпендикулярно плоскости основания и SC=АС=ВС. На ребрах SB и SС взяты соответственно точки E и F – середины этих ребер. Найти угол между прямыми СЕ и AF.

На ребрах А 1 В 1 и АС прямой призмы АВСА 1 В 1 С 1 , у которой АС=ВС=АА 1 и угол АСВ=90 о , взяты соответственно точки D и Е – середины ребер АВ и ВС. Найти угол между прямыми А 1 С и BD.

В правильной призме ABCDA 1 B 1 C 1 D 1 угол между диагоналями BD 1 и B 1 D равен 90 о . Найти угол, который образует прямая B 1 D с прямой А 1 С 1 .

Пример 19 . SАBCD – четырехугольная пирамида, основание которой – параллелограмм ABCD. Точка О – середина ребра SC. Постройте угол между прямыми DO и ВС.

Дано: SАBCD – четырехугольная пирамида, SO=OC.

Построить: ∠ (DО, ВC)

Рассмотрим плоскость α, которая проходит через точку О ∈ DC и прямую DF.

Эта плоскость пересекает ребро SB в точке К (FK║AB).

В этой плоскости через точку О проведем прямую, параллельную прямой DF (прямая ОК).

Таким образом, угол между скрещивающимися прямыми SO и DF есть угол между пересекающимися прямыми SO и ОК.

Пример 20 . ABCDA 1 B 1 C 1 D 1 – куб. Постройте угол между прямыми B 1 D и D 1 C.

Дано: ABCDA 1 B 1 C 1 D 1 – куб

Построить: ∠ (B 1 D, D 1 C)

В плоскости α, проходящей через точку D ∈ B 1 D и прямую D 1 C (плоскость грани DD 1 C 1 C), проведем прямую DK, параллельную прямой D 1 С. Тогда угол между скрещивающимися прямыми В 1 D и D 1 С есть угол между пересекающимися прямыми В 1 D и DК.

Расстояние между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми определяется как кратчайшее расстояние между точками этих прямых – оно равно длине их общего перпендикуляра.

Это расстояние равно расстоянию от одной из скрещивающихся прямых до плоскости, которая проходит через другую прямую параллельно первой.

Пример 21 . Дан куб ABCDA 1 B 1 C 1 D 1 . Найдите расстояние между прямыми АВ 1 и CD 1 , если длина ребра куба 4 см.

Дано: ABCDA 1 B 1 C 1 D 1 – куб,

Найти: ( АВ 1 ; CD 1 )

Расстояние между прямыми CD 1 и АВ 1 есть расстояние от любой точки прямой CD 1 до плоскости АВВ 1 .

Отрезок D 1 A 1 – перпендикуляр, проведенный из точки D 1 к плоскости АВВ 1 : D 1 A 1 ⊥ A 1 B 1 , D 1 A 1 ⊥ AA 1 , значит, D 1 A 1 ⊥ ( АВВ 1 ).

Следовательно, его длина равна расстоянию между прямыми АВ 1 и CD 1 , т.е. 4 см.

Пример 22 . В основании пирамиды МАВС лежит равнобедренный треугольник с прямым углом при вершине С . Высота пирамиды проектируется в точку О — середину ребра АВ , и ∠ АМВ =90°. На ребре МА взята точка Р — середина этого ребра, а в грани МВС взята точка Q , в которой пересекаются медианы грани МВС . Найдите расстояние между прямыми АВ и PQ , если ВС = а .

Дано: МАВС – пирамида, ∠ АМВ =90°, МР = РА .

В плоскости МАВ через точку Р проведем прямую РК || АВ.

Построим плоскость β , определяемую прямыми PQ и РК. Так как точка Q — точка пересечения медиан треугольника МВС, то прямая KQ пройдет через вершину С.

Таким образом, в сечении пирамиды плоскостью β мы получаем треугольник СКР. Так как прямая АВ || РК, то прямая АВ параллельна плоскости СКР.

Найдем расстояние от точки О до плоскости СКР. Для этого через точку О проведем плоскость γ, перпендикулярную прямой РК, лежащей в плоскости СКР.

Так как прямая РК || АВ, то плоскость γ перпендикулярна и прямой АВ.

Итак, в плоскости МАВ прямая ОМ перпендикулярна прямой АВ и в плоскости ABC прямая ОС перпендикулярна прямой АВ. Тогда плоскость, определяемая пересекающимися прямыми ОМ и ОС — это и есть плоскость γ перпендикулярная прямой АВ, т.е. и прямой РК.

Находим линию пересечения плоскостей СКР и γ — прямую CL. Расстояние от точки О до прямой CL равно расстоянию между скрещивающимися прямыми АВ и PQ. Найдем его как высоту прямоугольного треугольника LCO.

Если ОН — высота этого треугольника, то OH ⋅ CL=OC ⋅ OL, где из прямоугольного треугольника ABC находим ОС=АВ/2=а /2, из прямоугольного треугольника МАВ OL=ОМ/2=а /4, и из прямоугольного треугольника LCO CL= =a /4.

Таким образом, ОН=ОС ⋅ OL/CL=a /10.

Пример 23. В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 АВ =3, АА 1 =4. Найдите расстояние между BD 1 и AD .

Дано: АВ =3; АА 1 =4

BD 1 и AD скрещиваются. Спроецируем эти прямые на плоскость грани АА 1 В 1 В . Получим точку А – проекцию прямой AD и прямую А 1 В – проекцию прямой BD 1 .

Расстояние между BD 1 и AD равно расстоянию от точки А до А 1 В , т.е. высоте АК прямоугольного треугольника АА 1 В :

Задание 6 . Решите задачу…

Ребро куба ABCDA l B l C l D l равно 5 см. Найдите расстояния между прямой B l D и прямой D 1 C.

На ребре СС 1 правильной призмы ABCDA 1 B 1 C 1 D 1 взяты соответственно точки Р 1 и Р 2 , такие, что СР 1 =Р 1 Р 2 =Р 2 С 1 . Считая АВ= см, а АА 1 =3АВ, найдите расстояние между прямыми В 1 С и DP 1 .

В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 AB=АА 1 =10 см, AD=20 см. На ребре СС 1 взята точка Р такая, что CP:CC 1 =1:3, а на ребре А 1 В 1 взята точка V — середина этого ребра. Найдите расстояния между прямой В 1 С 1 и прямой PV.

На ребрах AB и В l С l куба ABCDA l B l C l D l взяты соответственно точки R и Q — середины этих ребер. Считая ребро куба равным 6 см, найдите расстояния между прямой B l D и прямой QR.

Все ребра прямой призмы АВСА 1 В 1 С 1 равны 2 см. На ребре АА 1 взята точка Р — середина этого ребра. Найдите расстояния между прямой АВ 1 и прямой СР.

На ребре СС 1 правильной призмы ABCDA 1 B 1 C 1 D 1 взяты соответственно точки Р 1 и Р 2 , такие, что СР 1 =Р 1 Р 2 =Р 2 С 1 . Считая АВ= см, а АА 1 =3АВ. Найдите расстояние между прямыми DC 1 и В 1 Р 1 .

В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 AB=АА 1 = см, AD=2 см. На ребрах СС 1 и AD взяты соответственно точки Р и Q, такие, что CP:CC 1 =AQ:AD=1:3. Найдите расстояния между прямой В 1 С 1 и прямой PQ.

Высота МО правильной пирамиды MABCD равна стороне ее основания и равна 3 см. На ребре МС взяты точки Р 1 , Р 2 и Р 3 , такие, что СР 1 =Р 1 Р 2 =Р 2 Р 3 =Р 3 М. Найдите расстояние между прямой АС и прямой DP 2 .

На ребре C 1 D 1 куба ABCDA 1 B 1 C 1 D 1 взята точка R — середина этого ребра. Ребро куба равно 6 см. Найдите расстояние между прямой B 1 D 1 и прямой DR.

На ребрах CD и В l С l куба ABCDA l B l C l D l взяты соответственно точки Р и Q — середины этих ребер. Считая ребро куба равным 2 см, найдите расстояния между прямой B l D и прямой PQ.

Сторона основания правильной треугольной призмы равна 3 cм, а косинус угла между прямыми, на которых лежат непересекающиеся диагонали двух смежных боковых граней призмы, равен 1/2. Найдите расстояния между этими прямыми.

На ребре DD 1 куба ABCDA 1 B 1 C 1 D 1 взята точка Q, такая, что DQ:DD 1 =2:3, а на диагонали А 1 В грани АВВ 1 А 1 взята точка P —середина А 1 В. Считая ребро куба равным 2 см, найдите расстояния между прямой DP и прямой C 1 Q .

На ребре СС 1 правильной призмы ABCDA 1 B 1 C 1 D 1 взяты соответственно точки Р 1 и Р 2 , такие, что СР 1 =Р 1 Р 2 =Р 2 С 1 . Считая АВ= см, а АА 1 =3АВ, найдите расстояние между прямыми В 1 С и DP 2 .

На ребре DD 1 куба ABCDA 1 B 1 C 1 D 1 взята точка Q, такая, что DQ:DD 1 =2:3, а на диагонали А 1 В грани АВВ 1 А 1 взята точка P —середина А 1 В. Считая ребро куба равным 3 см, найдите расстояния между прямой DP и прямой С 1 A 1.

Высота МО правильной пирамиды MABCD равна стороне ее основания и равна 6 см. На ребре МС взяты точки Р 1 , Р 2 и Р 3 , такие, что СР 1 =Р 1 Р 2 =Р 2 Р 3 =Р 3 М. Найдите расстояние между прямой АС и прямой DP 1 .

Все ребра прямой призмы АВСА 1 В 1 С 1 равны 2 см. На ребре СС 1 взята точка Q — середина этого ребра. Найдите расстояния между прямой АВ 1 и прямой BQ.

На ребре АВ куба ABCDA 1 B 1 C 1 D 1 взята точка Р — середина этого ребра. Ребро куба равно 4 см. Найдите расстояние между прямой B 1 D 1 и прямой DP.

Все ребра прямой призмы АВСА 1 В 1 С 1 равны см. Найдите расстояния между прямой АВ 1 и прямой ВС.

В основании пирамиды SABC лежит треугольник с прямым углом при вершине С и АС= см, ВС=2 см, а боковое ребро SC перпендикулярно плоскости и SC=BC. На ребрах АВ, SB и SC взяты соответственно точки Р, М и D –середины этих ребер. Найдите расстояние между прямыми АМ и РD.

На ребре DD 1 куба ABCDA 1 B 1 C 1 D 1 взята точка Q, такая, что DQ:DD 1 =2:3, а на диагонали А 1 В грани АВВ 1 А 1 взята точка P —середина А 1 В. Считая ребро куба равным см, найдите расстояния между прямой DP и прямой C 1 D 1 .

Сторона основания правильной треугольной призмы равна 18 cм, а косинус угла между прямыми, на которых лежат непересекающиеся диагонали двух смежных боковых граней призмы, равен -5/13. Найдите расстояния между этими прямыми.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Скрещивающиеся прямые. Проведение через одну из скрещивающихся прямых плоскости, параллельной другой прямой

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы рассмотрим определение скрещивающихся прямых и докажем теорему – признак скрещивающихся прямых. Далее рассмотрим три случая взаимного расположения двух прямых в пространстве. Докажем теорему о том, что через каждую из скрещивающихся прямых можно провести плоскость, параллельную другой прямой.
В конце урока решим несколько задач в тетраэдре на скрещиваемость прямых.