Взаимное расположение прямых параллельные и перпендикулярные прямые свойства (8 видео)

Геометрия. 7 класс

Содержание

Прямая. Параллельные и перпендикулярные прямые.
теория по математике 📈 планиметрия
Обозначения прямой
Признаки параллельности прямых
Аксиома параллельных прямых
Следствия из аксиом параллельных прямых
Перпендикулярные прямые
Взаимное расположение прямых параллельные и перпендикулярные прямые свойства
💥 Видео

Конспект урока

Параллельные и перпендикулярные прямые

Перечень рассматриваемых вопросов:

Взаимное расположение прямых на плоскости.
Параллельные прямые.
Аксиома параллельных прямых.
Перпендикулярные прямые.
Расстояние от точки до прямой, между параллельными прямыми.

Параллельные прямые – две прямые на плоскости называются параллельными, если они не пересекаются.

Перпендикулярные прямые – две прямые называются перпендикулярными, если при пересечении они образуют четыре прямых угла.

Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Взаимное расположение двух прямых на плоскости.

Вспомните, как могут располагаться на плоскости две прямые.

Две прямые на плоскости называются параллельными, если они не пересекаются.

Аксиома параллельных прямых: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Углы, изображенные на рисунке:

Накрест лежащие: 3 и 5; 4 и 6.

Соответственные: 1 и 5; 2 и 6; 3 и 8; 4 и 7.

Односторонние: 3 и 6; 4 и 5.

Признаки и свойства параллельных прямых.

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

Это признаки параллельности прямых. Обратные теоремы верны и представляют свойства параллельных прямых.

Способ построения параллельных прямых:

Аксиома параллельных прямых.

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

Если две прямые параллельны третьей, то они параллельны.

Если две прямые, пересекаясь, образуют четыре прямых угла, они называются перпендикулярными.

Прямые а и b на рисунке перпендикулярны: а ⏊ b.

Через каждую точку можно провести прямую, перпендикулярную данной и притом только одну.

Это можно сделать, пользуясь угольником или транспортиром.

Перпендикулярность и параллельность прямых.

Две прямые, перпендикулярные к третьей не пересекаются т. е параллельны между собой.

Отрезок АВ, перпендикулярный к прямой а, называют перпендикуляром. Точка В – основание перпендикуляра.

Из любой точки, не лежащей на данной прямой, можно опустить перпендикуляр на эту прямую и притом только один.

Длину перпендикуляра АВ называют расстоянием от точки А до прямой а.

Расстоянием между параллельными прямыми называют расстояние АВ от любой точки одной прямой до другой прямой.

Разбор заданий тренировочного модуля.

Решение: ∠1 и ∠2 соответственные, по свойству параллельных прямых: ∠1 = ∠2 = 220°: 2 = 110°.
∠2 и ∠3 смежные, по свойству смежных углов: ∠2 + ∠3 = 180° значит, ∠3 = 180° – 110° = 70°.

№ 2. Докажите, что биссектрисы смежных углов перпендикулярны.

Пусть ∠АОВ и ∠ВОС – смежные углы. ОК и ОР – их биссектрисы.
∠KOP = ∠КОВ + ∠ВОР. Поскольку ОК и ОВ – биссектрисы, то ∠КОВ = 1/2∠АОВ, ∠ВОР = 1/2∠ВОС по определению биссектрисы.
Тогда ∠КОР = 1/2∠АОВ + 1/2∠ВОС = 1/2(∠АОВ + ∠ВОС) = 180° : 2 = 90°.
Итак, ОК ⏊ ОР т. е. прямые перпендикулярны.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Прямая. Параллельные и перпендикулярные прямые.

теория по математике 📈 планиметрия

Линия, которую изображают на плоскости при помощи линейки, причем, эта линия не должна быть ограничена точкой ни с одной стороны, называют прямой. Другими словами, прямая не имеет ни начала, ни конца.

Обозначения прямой

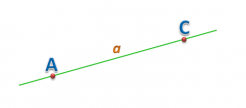
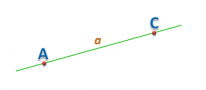
Обычно прямые обозначают прописной латинской буквой или двумя заглавными (если на прямой лежат точки). Рассмотрим это на рисунке. Данную прямую мы можем назвать двумя способами: прямая а; прямая АС.

Рассмотрим теперь две прямые на плоскости. Для них существует два случая расположения: пересекаются и не пересекаются.

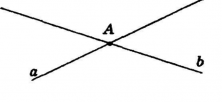
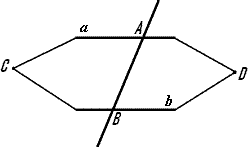
Если две прямые пересекаются, то есть имеют общую точку, то их называют пересекающимися. На рисунке показаны прямые а и b, которые пересекаются в точке A. Запись с помощью символов для данного рисунка выполняют следующим образом: а ∩ b=А, где ∩ — это знак «пересечение».

Если две прямые на плоскости не пересекаются, то их называют параллельными прямыми. На рисунке изображены параллельные прямые. Запись осуществляется следующим образом: a | | b, где | | — знак параллельности.

Признаки параллельности прямых

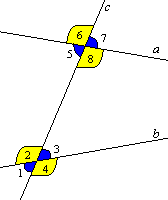
Рассмотрим прямую с, которая пересекает две прямые а и b и образует с ними восемь углов. Такую прямую с называют — секущая. Пары углов, которые образует секущая, также имеют названия. Итак, на данном рисунке изображены эти все прямые и восемь углов.

Необходимо запомнить названия следующих углов:

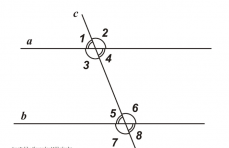
накрест лежащие углы: 4 и 5; 3 и 6;
односторонние углы: 4 и 6; 3 и 5;
соответственные углы: 1 и 5; 3 и 7; 2 и 6; 4 и 8.

С данными углами связаны следующие признаки параллельности прямых:

если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны;
если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны;
если при пересечении двух прямых секущей сумма внутренних односторонних углов равна 180 0 , то прямые параллельны.

Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

Аксиома параллельных прямых

Вспомним, что аксиомой принято называть утверждения, не требующие доказательств.

Через любые две точки на плоскости проходит прямая и притом только одна.

Аксиома №2 Через точку, не лежащую на данной прямой, можно провести только одну прямую параллельную данной.

Видео:Перпендикулярные прямые. 6 класс.Скачать

Следствия из аксиом параллельных прямых

Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

На данном рисунке видно, что а и b параллельные прямые, с – секущая, она пересекает прямую а в точке А, значит и будет пересекать прямую b в некоторой точке С.

Если две прямые параллельны третьей, то они параллельны.

По данному рисунку видно, что если прямая CD параллельна АВ и прямая MN параллельна АВ, то CD и MN тоже будут параллельны.

Видео:Математика 6 класс: Параллельные и перпендикулярные прямыеСкачать

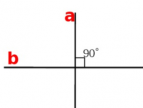
Перпендикулярные прямые

Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.

На рисунке показаны такие прямые а и b. Запись с помощью символов можно сделать следующим образом: а ⊥ b, где « ⊥ » — знак перпендикулярности. Заметим, что две прямые, перпендикулярные к третьей, не пересекаются. На данном рисунке а ⟂ с, b ⟂ c. Видно, что прямые а и b не пересекаются, то есть они – параллельны.

Видео:Геометрия 7 класс (Урок№33 - Повторение. Параллельные и перпендикулярные прямые.)Скачать

Взаимное расположение прямых параллельные и перпендикулярные прямые свойства

Определение.1. Параллельные прямое
Определение.2. Перпендикулярные прямые
Теорема.1. I свойство параллельных прямых
Теорема.2. II свойство параллельных прямых
Теорема.3. III свойство параллельных прямых
Теорема.4. IV свойство параллельных прямых
Теорема.5. V свойство параллельных прямых
Теорема.6. I признак параллельных прямых
Теорема.7. II признак параллельных прямых
Теорема.8. III признак параллельных прямых
Теорема.9. IV признак параллельных прямых
Теорема 10. V признак параллельных прямых
Теорема 11. Две прямые, параллельные третей
Теорема 11.1 Следствие
Теорема 12. Прямая, пересекающая одну из параллельных прямых
Теорема 13. Отрезки параллельных прямых
Теорема 14. Теорема Фалеса
Теорема 14.1. Параллельные прямые, пересекающие стороны угла
Теорема 15. Прямая, перпендикулярна одной из параллельных прямых
Теорема 16. Две (и более) прямые, перпендикулярные третей прямой

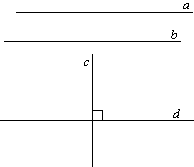
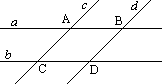
Определение 1. Параллельными называются прямые, которые не пересекаются, сколько бы мы их не продолжали.
На рисунке a и b.

Определение 2. Перпендикулярными называются прямые, которые пересекаются под прямым углом.
На рисунке c и d.
При пересечении пары прямых (параллельных в данном случае) некой прямой (такая прямая называется секущей прямой) образуются (акромя пройденных нами в теме углы смежных и вертикальных) следующие углы:
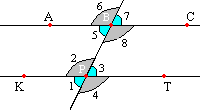
Внутренние накрестлежащие углы — 2 и 8; 3 и 5
Внешние накрестлежащие углы — 1 и 7; 4 и 6
Внутренние односторонние углы — 2 и 5; 3 и 8
Внешние односторонние углы — 1 и 6; 4 и 7
Соответственные углы — 1 и 5; 2 и 6; 3 и 7; 4 и 8
Между этими углами можно вывести закономерности. Свойства параллельных прямых:
Теорема 1. Внутренние накрестлежащие углы равны

Доказательство: Пусть a и b — две параллельные прямые, c — секущая, A и B — точки пересечения секущей с этими прямыми. Пусть утверждение теоремы ложно. Проведем тогда через точку A прямую d, такую что внутренние накрест лежащие углы при прямых b и d и секущей c равны. Тогда по первому признаку параллельности прямых, прямые b и d параллельны. Но прямые b и a параллельны. Значит, через точку A проходят две прямые — a и d, параллельные прямой b. Это противоречит IX аксиоме. Значит, утверждение теоремы верно. Теорема доказана.
Теорема 2. Внешние накрестлежащие углы равны

Доказательство: Очевидно из первого свойства параллельных прямых.
Теорема 3. Сумма внутренних односторонних углов равна 180 градусам

Доказательство: Очевидно из первого свойства параллельных прямых.
Теорема 4. Сумма внешних односторонних углов равна 180 градусам

Доказательство: Очевидно из первого свойства параллельных прямых.
Теорема 5. Соответственные углы равны

Доказательство: Очевидно из первого свойства параллельных прямых.

Теорема 6. Если при пересечении двух прямых а и b третей прямой с внутренние накрестлежащие углы равны (одна пара), то такие прямые а и b являются параллельными

Доказательство: Пусть прямые a и b пересекаются секущей в точках A и B, но прямые a и b пересекаются в точке C (рис. 15). Секущая c разбивает плоскость на две полуплоскости. В одной из них лежит точка C. Построим треугольник ABD, равный треугольнику ABC, с вершиной D в другой полуплоскости. Угол DAB равен углу ABC, а значит, точка D лежит на прямой a по условию. Аналогично точка D лежит на прямой b. Следовательно, точка D принадлежит прямым a и b. Значит, прямые a и b пересекаются в двух точках — C и D. Противоречие. Значит, исходное предположение не верно. Теорема доказана.
Теорема 7. Если при пересечении двух прямых а и b третей прямой с внешние накрестлежащие углы равны (одна пара), то такие прямые а и b являются параллельными

Доказательство: Очевидно из первого признака параллельности прямых.
Теорема 8. Если при пересечении двух прямых а и b третей прямой с сумма внутренних односторонних углов равна 180 градусам (одна пара), то такие прямые а и b являются параллельными

Доказательство: Очевидно из первого признака параллельности прямых.
Теорема 9. Если при пересечении двух прямых а и b третей прямой с сумма внешних односторонних углов равна 180 градусам (одна пара), то такие прямые а и b являются параллельными

Доказательство: Очевидно из первого признака параллельности прямых.
Теорема 10. Если при пересечении двух прямых а и b третей прямой с соответственные углы равны (одна пара), то такие прямые а и b являются параллельными

Доказательство: Очевидно из первого признака параллельности прямых.
Теорема 11. Две прямые, параллельные третей, параллельны.

Доказательство: Пусть прямые a и b параллельны прямой c. Допустим, что прямые a и b не па-раллельны. Тогда либо прямые a и b совпадают, что противоречит условию, либо пересекаются в не-которой точке S. Тогда через точку S проходит две прямые — a и b, параллельные прямой c, что противоречит IX аксиоме. Значит, исходное предположение не верно. Теорема доказана.
Теорема 11.1. Если параллельно одной из двух параллельных прямых провести третью прямую, вторая из этих прямых либо параллельна третьей, либо совпадает с ней.

Доказательство: Очевидно из теоремы 11 параллельности прямых.
Теорема 12. Если прямая пересекает одну из параллельных прямых, то она пересекает и вторую.
Теорема 13. Отрезки параллельных прямых, заключенные между некой (иной) парой параллельных прямых, равны.
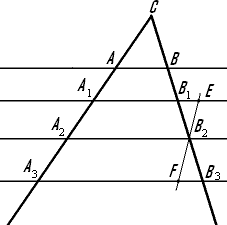
Теорема 14. (Теорема Фалеса) Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Доказательство: Пусть A₁, A₂, A₃ — точки пересечения параллельных прямых с одной из сторон угла, и точка A₂ лежит между точками A₁ и A₃. Пусть B₁, B₂, B₃ — соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если A₁A₂ = A₂A₃, то B₁B₂ = B₂B₃. Проведем через точку B₂ прямую EF, параллельную прямой A₁A₃. Треугольники EB₂B₁ и FB₂B₃ равны по второму признаку равенства треугольников. У них стороны EB₂ и FA₂ равны по условию, углы B₁B₂E и B₃B₂F равны как вертикальные, а углы B₁EB₂ и B₂FB₃ равны как внутренние накрест лежащие при секущей EF. Значит, B₁B₂ = B₂B₃. Что и требовалось доказать.
Теорема 14.1.. Параллельные прямые, пересекая стороны угла, отсекают пропорциональные отрезки.

Теорема 15. Две (и более) прямые, перпендикулярные третей прямой, параллельны.

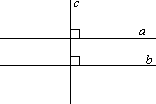
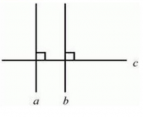
Доказательство: Действительно, внутренние накрест лежащие углы равны 90°. Следовательно, по первому признаку параллельных прямых, эти прямые параллельны.
Теорема 16. Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй.

Доказательство: Очевидно из теоремы 15.