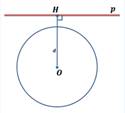
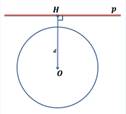
Взаимное расположение прямой и окружности ответы (3 видео)

Взаимное расположение прямой и окружности

Выясним количество общих точек прямой и окружности в зависимости от их взаимного расположения. Если прямая l проходит через центр O окружности (Рис.1), то она пересекает окружность в двух точках, которые являются концами диаметра окружности.

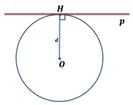
Пусть прямая не проходит через центр окружности. Проведем перпендикуляр OH к прямой l (Рис.2, Рис.3, Рис.4). Обозначим расстояние от центра окружности до прямой l буквой d. Рассмотрим сколько общих точек будут иметь прямая и окружность в зависимости от соотношения d и r.

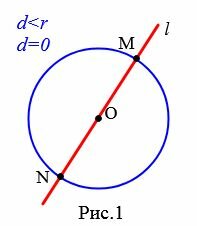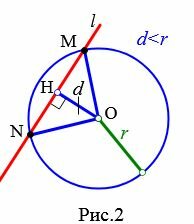Взаимное расположение прямой и окружности ответы

Теорема 1. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.

В этом случае прямая называется секущей по отношению к окружности.

Доказательство. Пусть расстояние от центра окружности до прямой меньше радиуса окружности: d Теорема 2. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.

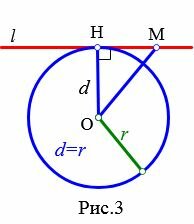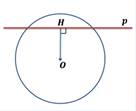
Доказательство. Пусть расстояние от центра окружности до прямой равно радиусу окружности: d=r (Рис.3). В этом случае OH=r, т.е. точка H лежит на окружности и является общей точкой прямой l и окружности. Возьмем на прямой l любую точку M отличной от H. Тогда расстояние от OM больше расстояния OH=r, поскольку наклонная OM больше перпендикуляра OH к прямой l. Следовательно точка M не лежит на окружности. Получили, что точка H единственная общая точка прямой l и окружности.

Теорема 3. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.

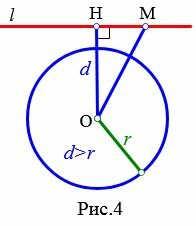Доказательство. Пусть расстояние от центра окружности до прямой больше радиуса окружности:d>r (Рис.4). Тогда ( small OH > r). Возьмем на прямой l любую точку M отличной от H. Тогда ( small OM > OH>r). Следовательно точка M не лежит на окружности. Таким образом, если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.

Видео:Геометрия 8 класс (Урок№25 - Взаимное расположение прямой и окружности.)Скачать

Тест: Взаимное расположение прямой и окружности

Взаимное расположение прямой и окружности

Сколько точек пересечения имеет окружность и секущая?

Сколько точек пересечения имеет окружность и касательная?

Укажите рисунок, на котором изображена секущая к окружности.

Выберите один из 3 вариантов ответа:

1) 2) 3)

Укажите рисунок, на котором изображена касательная к окружности.

Выберите один из 3 вариантов ответа:

1) 2) 3)

Составьте верные соответствия между соотношением расстояния от центра окружности до прямой ( d ) и радиусам окружности ( r ):

Укажите соответствие для всех 3 вариантов ответа:

1) прямая и окружность имеют две общие точки

2) прямая и окружность не имеют общих точек

3) прямая и окружность имеют одну общую точку

Определить взаимное расположение прямой и окружности, если:

Выберите один из 3 вариантов ответа:

1) прямаяи окружность не пересекаются

2) прямая является касательной к окружности

3) прямая является секущей к окружности

Определить взаимное расположение прямой и окружности, если:

Выберите один из 3 вариантов ответа:

1) прямаяи окружность не пересекаются

2) прямая является касательной к окружности

3) прямая является секущей к окружности

Определить взаимное расположение прямой и окружности, если:

Выберите один из 3 вариантов ответа:

1) прямаяи окружность не пересекаются

2) прямая является касательной к окружности

3) прямая является секущей к окружности

Определить взаимное расположение прямой и окружности, если:

d = 2015, r = 2014

Выберите один из 3 вариантов ответа:

1) прямаяи окружность не пересекаются

2) прямая является касательной к окружности

3) прямая является секущей к окружности

Определить взаимное расположение прямой и окружности, если:

d = 2014, r = 2015

Выберите один из 3 вариантов ответа:

1) прямаяи окружность не пересекаются

2) прямая является касательной к окружности

Видео:Взаимное расположение окружности и прямой. 7 класс.Скачать

Геометрия. 8 класс

Конспект
Рассмотрим окружность с центром в точке О и прямую a, её не пересекающую.
Расстояние от центра окружности до прямой равно длине перпендикуляра ОВ.

Это расстояние больше радиуса окружности.
Будем перемещать прямую, параллельно самой себе в сторону центра окружности. В определённый момент, прямая коснется окружности.

Расстояние от центра окружности до прямой равно радиусу окружности.
Прямая, имеющая с окружностью только одну общую точку называется касательной к окружности.
Общая точка прямой и окружности называется точкой касания.
Будем передвигать прямую далее к центру. Прямая пересечет окружность в двух точках.
Расстояние от центра окружности до прямой меньше радиуса.

Продолжая движение дальше, мы получим еще одну касательную к окружности.

Продолжим движение прямой дальше, она опять не будет иметь с окружностью общих точек.
Расстояние от центра окружности опять больше её радиуса.

Рассмотрим случай, когда прямая имеет с окружностью одну общую точку.

Сформулируем свойство касательной.
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Дано: Окружность с центром О, a – касательная, B – точка касания.
Доказать: a ⊥ OB
Доказательство:
Пусть утверждение неверно, т.е. прямая a не перпендикулярна радиусу OB. Тогда OB – наклонная к прямой a. Перпендикуляр меньше наклонной, тогда расстояние от центра O до прямой a меньше радиуса. Следовательно, прямая a и окружность имеют 2 общие точки. Но это противоречит условию, т.к. прямая a – касательная. Значит наше предположение неверно и a ⊥ OB.
Верно и обратное утверждение:
Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Проведем к окружности две касательные из одной точки, не принадлежащей окружности.

Выполняется утверждение:
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Докажите его самостоятельно, используя равенство треугольников AOВ и AOС.
Дано: окружность с центром O, касательные AB и AC
Доказать: AB = AC, ∠OAB = ∠OAC
Геометрия, 7-9: учеб. для общеобразоват. учреждений/ [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. – М.: Просвещение, 2017.