- Python Basic — 1: Упражнение 45 с решением
- Вычислительная геометрия
- Русско-английский тематический словарик
- Упражнения на векторные и скалярные произведения
- 01: Расстояние между двумя точками
- 02: Полярный угол точки
- 03: Угол между векторами
- 04: Площадь треугольника
- 05: Классификация векторов
- 06: Три точки
- 07: Принадлежность точки лучу
- 08: Принадлежность точки отрезку
- 09: Расстояние от точки до луча
- 10: Расстояние от точки до отрезка
- 11: Принадлежит ли точка углу
- 12: Пересекаются ли два луча
- 13: Пересекаются ли два отрезка
- Упражнения на уравнение прямой
- 14: Уравнение прямой
- 15: Перпендикулярная прямая
- 16: Принадлежность точки прямой
- 17: Взаимное расположение двух точек
- 18: Классификация прямых
- 19: Расстояние от точки до прямой
- 20: Параллельная прямая
- 21: Основание перпендикуляра
- 22: Пересечение двух прямых — 1
- 23: Пересечение двух прямых — 2
- Упражнения на треугольники
- 24: Биссектриса угла
- 25: Точка пересечения медиан
- 26: Точка пересечения биссектрис
- 27: Точка пересечения высот
- 28: Точка пересечения срединных перпендикуляров
- 29: Вписанная окружность
- 30: Описанная окружность
- 31: Принадлежность точки треугольнику
- 32: Минимальная окружность
- 33: Расстояние от прямой до окружности
- 34: Пересечение прямой и окружности
- 35: Угол обзора
- 36: Поворот точки
- 37: Поворот прямой
- 38: Точки касания
- 39: Длина дуги
- 40: Пересечение окружностей
- Задачи на многоугольники
- 41: Площадь многоугольника
- 42: Выпуклость многоугольника
- 43: Принадлежность точки многоугольнику
- 44: Принадлежность точки выпуклому многоугольнику
- Разные задачи
- 45: Ловушка для Слонопотама
- 46: Воздушный шарик
- 47: Космический кегельбан
- 48: Кольцевая автодорога
- Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2
- Вступление
- 🎬 Видео
Видео:Взаимное расположение окружностей. 7 класс.Скачать

Python Basic — 1: Упражнение 45 с решением
Есть две окружности C1 с радиусом r1, центральной координатой (x1, y1) и C2 с радиусом r2 и центральной координатой (x2, y2)
Напишите программу на Python, чтобы проверить следующее:
- «C2 находится в C1», если C2 находится в C1
- «C1 находится в C2», если C1 находится в C2
- «Окружность С1 и С2 пересекаются», если пересекаются С1 и С2, и
- «C1 и C2 не перекрываются», если C1 и C2 не перекрываются.
Входные данные :
Входные числа (действительные числа) разделяются пробелом.
Иллюстрированная презентация:
Пример решения :
Код Python:
Блок — схема:
Редактор кода Python:
Есть другой способ решить это решение? Внесите свой код (и комментарии) через Disqus.
Каков уровень сложности этого упражнения?
Видео:Геометрия 9 класс (Урок№10 - Взаимное расположение двух окружностей.)Скачать

Вычислительная геометрия
Для тех, кто допускает, что его жизнь будет так или иначе связана с программированием, рекомендуется создавать классы для базовых примитивов (точка, вектор, прямая, луч, окружность и т.п.) и определять соответствующие операции с ними. Например, разность двух точек может давать вектор, вектора можно скалярно и векторно перемножать. Сами вектора можно умножать на числа, складывать и вычитать. Прямую можно собрать по двум точкам, по точке и вектору, которому прямая должна быть параллельна или перпендикулярна. Функция «Пересечение» может выдавать список точек (возможно, пустой) И т.п. Здесь хороший простор для продумывания удобной архитектуры решения.
Видео:Взаимное расположение двух окружностей. Урок 8. Геометрия 9 классСкачать

Русско-английский тематический словарик
| точка | point |
| вектор | vector |
| прямая | line |
| луч | ray |
| отрезок | segment |
| угол | angle |
| окружность | circle |
| треугольник | triangle |
| прямоугольник | rectangle |
| квадрат | square |
| многоугольник | polygon |
| окружность | circle |
| медиана | median |
| биссектриса | bissector |
| высота | altitude |
| пересечение | intersection |
| длина | length |
| периметр | perimeter |
| площадь | area |
| касательная | tangent |
| скалярное произведение | dot product |
| векторное произведение | cross product |
| вектор нормали | normal vector |
Видео:Геометрия 16-09. Взаимное расположение двух и более окружностей. Задача 9Скачать

Упражнения на векторные и скалярные произведения
01: Расстояние между двумя точками
Даны координаты двух точек. Найдите расстояние между ними.
| Ввод | Вывод |
|---|
02: Полярный угол точки
Даны два числа – координаты точки, не совпадающей с началом координат. Выведите ее полярный угол (величину от 0 до $2pi$).
| Ввод | Вывод |
|---|
03: Угол между векторами
Даны четыре числа: координаты двух невырожденных векторов.
Выведите величину неориентированного угла между ними.
| Ввод | Вывод |
|---|
04: Площадь треугольника
Даны шесть чисел: координаты трех вершин треугольника.
Выведите значение площади треугольника.
| Ввод | Вывод |
|---|
05: Классификация векторов
Даны четыре числа: координаты двух ненулевых векторов. Если эти вектора коллинеарны, выведите 1. Если эти вектора перпендикулярны, выведите 2. Иначе выведите 0.
В этой задаче нельзя использовать обратные тригонометрические функции.
| Ввод | Вывод |
|---|
06: Три точки
Программа получает на вход шесть чисел: координаты трех точек.
Программа должна вывести YES , если эти точки лежат на одной прямой, или NO в противном случае.
| Ввод | Вывод |
|---|
07: Принадлежность точки лучу
Программа получает на вход шесть чисел: координаты точки и координаты начала и конца вектора. Проверьте, принадлежит ли данная точка лучу, задаваемому данным вектором.
Программа должна вывести YES , если точка принадлежит лучу, или NO в противном случае.
| Ввод | Вывод |
|---|
08: Принадлежность точки отрезку
Программа получает на вход шесть чисел: координаты точки и координаты концов отрезка. Проверьте, принадлежит ли данная точка данному отрезку.
Программа должна вывести YES , если точка принадлежит отрезку, или NO в противном случае.
| Ввод | Вывод |
|---|
09: Расстояние от точки до луча
Дано шесть чисел: координаты точки, координаты начала и конца вектора.
Программа должна вывести единственное число: расстояние от точки до луча, заданного вектором.
| Ввод | Вывод |
|---|
10: Расстояние от точки до отрезка
Дано шесть чисел: координаты точки и координаты двух концов отрезка.
Программа должна вывести единственное число: расстояние от данной точки до данного отрезка.
| Ввод | Вывод |
|---|
11: Принадлежит ли точка углу
Дан угол AOB (O — вершина угла, A и B — точки на сторонах) и точка P. Определите, принадлежит ли точка P углу AOB (включая его стороны: лучи OA и OB).
Программа получает на вход координаты точек A, O, B, P. Все координаты — целые, не превосходят 100 по модулю. Точки A, O, B не лежат на одной прямой.
Программа должна вывести слово YES или NO.
| Ввод | Вывод |
|---|
12: Пересекаются ли два луча
Даны два луча: AB и CD (A и C — вершины лучей, B и D лежат на лучах). Проверьте, пересекаются ли они.
Программа получает на вход координаты точек A, B, C, D. Все координаты — целые, не превосходят 100 по модулю.
Программа должна вывести слово YES или NO.
| Ввод | Вывод |
|---|
13: Пересекаются ли два отрезка
Даны два отрезка AB и CD. Проверьте, пересекаются ли они.
Программа получает на вход координаты точек A, B, C, D. Все координаты — целые, не превосходят 100 по модулю.
Программа должна вывести слово YES или NO.
| Ввод | Вывод |
|---|
Видео:Алгоритмы. Пересечение окружностейСкачать

Упражнения на уравнение прямой
14: Уравнение прямой
Прямая задана двумя точками. Выведите коэффициенты A, B, C нормального уравнения прямой.
| Ввод | Вывод |
|---|
15: Перпендикулярная прямая
Дано уравнение прямой и координаты точки. Выведите коэффициенты уравнения прямой, перпендикулярной данной прямой и проходящей через данную точку.
| Ввод | Вывод |
|---|
16: Принадлежность точки прямой
Даны координаты точки и уравнение прямой. Определите, принадлежит ли точка прямой, выведите YES или NO.
| Ввод | Вывод |
|---|
17: Взаимное расположение двух точек
Даны две точки и уравнение прямой, точки не лежат на прямой. Выведите YES, если точки лежат по одну сторону от прямой и NO в противном случае.
| Ввод | Вывод |
|---|
18: Классификация прямых
Программа получает на вход шесть чисел: коэффициенты уравнений двух прямых.
Программа должна вывести 1, если эти прямые совпадают, 2 – если параллельны, 3 – если перпендикулярны и 0 во всех остальных случаях.
| Ввод | Вывод |
|---|
19: Расстояние от точки до прямой
Даны пять чисел: координаты точки и коэффициенты нормального уравнения прямой.
Программа должна вывести одно число: расстояние от данной точки до данной прямой.
| Ввод | Вывод |
|---|
20: Параллельная прямая
Даны четыре числа: коэффициенты нормального уравнения прямой и величина d.
Программа должна вывести три числа: коэффициенты нормального уравнения любой из прямых, паралелльных данной, и лежащих от нее на расстоянии d.
| Ввод | Вывод |
|---|
21: Основание перпендикуляра
Дано пять чисел: координаты точки и коэффициенты нормального уравнения прямой.
Программа должна вывести два числа: координаты основания перпендикуляра, опущенного из данной точки на данную прямую
| Ввод | Вывод |
|---|
22: Пересечение двух прямых — 1
Дано шесть чисел: коэффициенты нормальных уравнений двух непараллельных прямых.
Программа должна вывести два числа: координаты точки пересечения данных прямых.
| Ввод | Вывод |
|---|
23: Пересечение двух прямых — 2
На плоскости даны две прямые. Каждая прямая задается парой точек, через которые она проходит. Требуется установить, пересекаются ли эти прямые, и найти координаты точки пересечения.
Вводятся сначала координаты двух различных точек, через которые проходит первая прямая, а затем — координаты еще двух различных (но, быть может, совпадающих с первыми двумя) точек, через которые проходит вторая прямая. Координаты каждой точки — целые числа, по модулю не превышающие 1000.
Если прямые не пересекаются, выведите одно число 0. Если прямые совпадают, выведите 2. Если прямые пересекаются ровно в одной точке, то выведите сначала число 1, а затем два вещественных числа — координаты точки пересечения.
| Ввод | Вывод |
|---|
Видео:Взаимное расположение двух окружностейСкачать

Упражнения на треугольники
Треугольник задается координатами трех точек — вершин треугольника.
24: Биссектриса угла
Даны координаты трех точек O, A, B. Постройте уравнение прямой, являющейся биссектрисой угла ∠AOB.
| Ввод | Вывод |
|---|
25: Точка пересечения медиан
Дан треугольник. Найдите точку пересечения его медиан.
| Ввод | Вывод |
|---|
26: Точка пересечения биссектрис
Дан треугольник. Найдите точку пересечения его биссектрис.
| Ввод | Вывод |
|---|
27: Точка пересечения высот
Дан треугольник. Найдите точку пересечения его высот.
| Ввод | Вывод |
|---|
28: Точка пересечения срединных перпендикуляров
Дан треугольник. Найдите точку пересечения его срединных перпендикуляров.
| Ввод | Вывод |
|---|
29: Вписанная окружность
Выведите радиус окружности, вписанной в данный треугольник.
| Ввод | Вывод |
|---|
30: Описанная окружность
Выведите радиус окружности, описанной вокруг данного треугольник.
| Ввод | Вывод |
|---|
31: Принадлежность точки треугольнику
Дан треугольник и точка. Выведите слово YES, если точка принадлежит треугольнику (она может лежать на границе треугольника) и слово NO в противном случае.
| Ввод | Вывод |
|---|
32: Минимальная окружность
Дан треугольник. Найдите минимальную окружность, содержащую внутри себя треугольник.
Выведите три числа: координаты центра и радиус данной окружности.
| Ввод | Вывод |
|---|
33: Расстояние от прямой до окружности
Даны шесть чисел: координаты центра окружности, ее радиус (в первой строке), коэффициенты нормального уравнения прямой (во второй строке).
Выведите единственное число: расстояние от данной окружности до данной прямой.
| Ввод | Вывод |
|---|
34: Пересечение прямой и окружности
Даны шесть чисел: координаты центра окружности, ее радиус (в первой строке), коэффициенты нормального уравнения прямой (во второй строке).
В первой строке одно число K, равное количеству точек пересечения прямой с окружностью. Далее в K строках координаты самих точек.
| Ввод | Вывод |
|---|
35: Угол обзора
Даны пять чисел: координаты центра окружности, ее радиус (в первой строке), координаты точки, лежащей вне окружности (во второй строке).
Выведите единственное число: угол (в радианах), под которым видна данная окружность из данной точки.
| Ввод | Вывод |
|---|
36: Поворот точки
Даны три числа: координаты точки и угол (в радианах, задан в виде действительного числа).
Выведите координаты точки, полученной поворотом данной точки вокруг начала координат на данный угол в положительном направлении.
| Ввод | Вывод |
|---|
37: Поворот прямой
Даны четыре числа: коээфициенты нормального уравнения прямой и угол (в радианах, задан в виде действительного числа).
Выведите три числа: коэффициенты нормального уравнения прямой, полученной поворотом данной прямой вокруг начала координат на данный угол в положительном направлении.
| Ввод | Вывод |
|---|
38: Точки касания
Даны пять чисел: координаты центра окружности, ее радиус (в первой строке), координаты точки (во второй строке).
Выведите одно число K, равное количеству точек пересечения всевозможных касательных к окружности, проходящих через данную точку. Далее в K строках координаты самих точек пересечения касательных с окружностью.
| Ввод | Вывод |
|---|
39: Длина дуги
Даны семь чисел – координаты центра и радиус окружности (в первой строке) и действительные координаты двух точек на ней (во второй и третьей строке), с точностью до пятого знака после запятой.
Выведите одно число: длину меньшей из дуг окружности, заключенной между указанными точками.
| Ввод | Вывод |
|---|
40: Пересечение окружностей
Даны шесть чисел – координаты центров и радиусы двух окружностей окружности.
В случае если количество общих точек окружностей конечно, в первой строке вывести одно число K, равное этому количеству, далее в K строках координаты самих точек. Если указанных точек бесконечно много, вывести единственное число «3».
| Ввод | Вывод |
|---|
Видео:Взаимное расположение окружностей. Практическая часть. 7 класс.Скачать

Задачи на многоугольники
41: Площадь многоугольника
Задан многоугольник: сначала задано количество вершин многоугольника N, не превосходящее 100.000, затем N вершин многоугольника в порядке обхода. Выведите единственное число: площадь многоугольника.
| Ввод | Вывод |
|---|
42: Выпуклость многоугольника
Задан многоугольник, как в предыдущей задаче. Выведите YES , если многоугольник является выпуклым и NO в противном случае.
| Ввод | Вывод |
|---|
43: Принадлежность точки многоугольнику
Первая строка входных данных содержит число N, 3≤N≤10 5 . Далее идет N точек – координаты вершин многоугольника. Затем идут координаты проверяемой точки. Программа должна вывести YES , если точка лежит внутри многоугольника или на его границе и NO в противном случае.
Координаты всех точек могут быть дробными числами!
| Ввод | Вывод |
|---|
44: Принадлежность точки выпуклому многоугольнику
Первая строка входных данных содержит число N, 3≤N≤10 5 . Далее идет N точек – координаты вершин выпуклого многоугольника. Затем записано число K , 3≤N≤10 5 – количество проверяемых точек. Затем в K строчках записаны координаты K проверяемых точек.
Для каждой проверяемой точки выведите YES , если точка лежит внутри многоугольника или на его границе и NO в противном случае.
Координаты всех точек могут быть дробными числами!
| Ввод | Вывод |
|---|
Видео:9 класс, 8 урок, Взаимное расположение двух окружностейСкачать

Разные задачи
45: Ловушка для Слонопотама
Пятачок и Винни-Пух каждое утро ходят пить чай в гости к Кролику. Естественно, самым коротким путем.
К сожалению, однажды Винни-Пуху пришла в голову идея вырыть ловушку для Слонопотама. Самое обидное, что они с Пятачком ее даже вырыли. Поэтому теперь каждое утро, идя в гости к Кролику, они боятся в нее провалиться.
Напишите программу, которая посчитает длину самого короткого безопасного пути от домика Винни-Пуха до домика Кролика.
Ловушка для Слонопотама представляет собой яму абсолютно круглой формы. Путь является безопасным, если он не проходит по ловушке (но может проходить по ее границе).
В первой строке входных данных записаны координаты домика Винни-Пуха $X_B$, $Y_В$, во второй строке — координаты домика Кролика $X_K$, $Y_K$, в третьей строке — координаты центра и радиус ловушки $X_L$, $Y_L$, $R_L$. Все координаты — целые числа из диапазона от –32000 до 32000. Радиус ловушки — натуральное число, не превышающее 32000.
Домики Винни-Пуха и Кролика не могут находиться внутри ловушки, но могут находиться на ее границе.
Выведите в выходной файл одно число — длину самого короткого безопасного пути от домика Винни-Пуха до домика Кролика с тремя знаками после точки.
| Ввод | Вывод |
|---|
46: Воздушный шарик
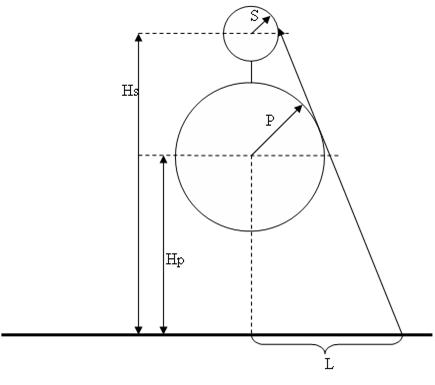
Винни Пух и Пятачок отправились воровать мед у пчел, и, в очередной раз влипли в неприятности. Пятачку опять потребовалось выстрелить из своего охотничьего ружья и пробить воздушный шарик, на котором Винни Пух поднялся к дуплу за медом. При этом желательно попасть именно в шарик, не задев медведя. Вычислите оптимальную позицию для стрельбы.
Поскольку Винни Пух очень любит покушать, то в данной задаче (да и не только в задаче) примем его за сферу радиуса $P$. Центр медведя находится на высоте $H_p$ над уровнем земли. Строго над медведем , находится еще одна сфера, радиуса $S$ — воздушный шарик; центр шарика находится на высоте $H_s$ над уровнем земли. Центры обеих сфер находятся на одной вертикальной прямой. По понятным причинам гарантируется, что сферы не пересекаются, однако могут касаться.
Считая, что ружье стреляет строго по прямой, вычислите минимальное расстояние $L$, на которое Пятачок должен отойти от места взлета, чтобы успешно поразить шарик. Шарик считается пораженным, если траектория пули хотя бы касается его поверхности; при этом если траектория пули касается медведя, то он считается невредимым.
Вводятся положительные целые числа $P$, $H_p$, $S$ и $H_s$, не превосходящие 10000.
Выведите минимальное расстояние от точки взлета, с которого можно поразить шарик из ружья.
| Ввод | Вывод |
|---|
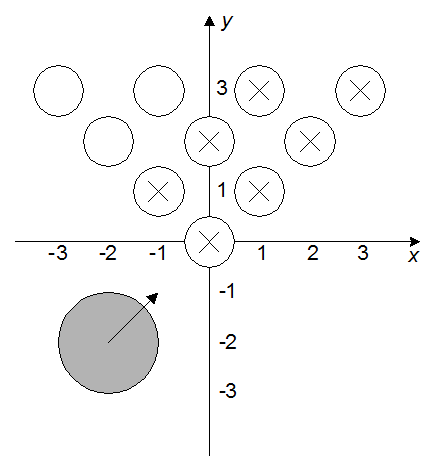
47: Космический кегельбан
На планете Плюк открылся новый космический кегельбан. Поле для кегельбана представляет собой бесконечную плоскость, на которой расставлены кегли.
Каждая кегля представляет собой высокий цилиндр с основанием в виде круга радиусом $r$ метров. Все кегли одинаковые. Кегли расставлены по следующим правилам. Кегли образуют $n$ рядов, в первом ряду стоит одна кегля, во втором — две, и так далее. В последнем $n$-м ряду стоит $n$ кеглей. Введем на плоскости систему координат таким образом, чтобы единица измерения была равна одному километру. Центр единственной кегли в первом ряду находится в точке $(0, 0)$. Центры кеглей во втором ряду находятся в точках $(–1, 1)$ и $(1, 1)$. Таким образом, центры кеглей в $i$-м ряду находятся в точках с координатами $(–(i – 1), i – 1)$, $(–(i – 3), i – 1)$, . $(i – 1, i – 1)$.
Игра происходит следующим образом. Используется шар с радиусом $q$ метров. Игрок выбирает начальное положение центра шара $(x_c, y_c)$ и вектор направления движения шара $(v_x, v_y)$. После этого шар помещается в начальную точку и двигается не останавливаясь в направлении вектора $(v_x, v_y)$. Считается, что шар сбил кеглю, если в процессе движения шара имеет место ситуация, когда у шара и кегли есть общая точка. Сбитые кегли не меняют направления движения шара и не сбивают соседние кегли при падении.
На рисунке приведен пример расположения кеглей для $r = 500$, $n = 4$ и шара для $q = 1000$, $x_c = –2$, $y_c = –2$, $v_x = 1$, $v_y = 1$.
Требуется написать программу, которая по заданным радиусу кегли $r$, количеству рядов кеглей $n$, радиусу шара $q$, его начальному положению $(x_c, y_c)$ и вектору направления движения $(v_x, v_y)$ определяет количество кеглей, сбитых шаром.
Первая строка входных данных содержит два целых числа: $r$ и $n$, разделенных ровно одним пробелом ($1 le r le 700$, $1 le n le 200000$).
Вторая строка входных данных содержит целое число $q$ ($1 le q le 10^9$).
Третья строка входных данных содержит два целых числа $x_c$ и $y_c$, разделенных ровно одним пробелом ($–10^6 le x_c le 10^6$, $–10^6 le y_c$, $1000y_c lt –(r + q)$).
Четвертая строка входных данных содержит два целых числа $v_x$ и $v_y$, разделенных ровно одним пробелом ($–10^6 le v_x le 10^6$, $0 lt v_y le 10^6$).
Программа должна вывести одно целое число — количество сбитых кеглей.
| Ввод | Вывод |
|---|
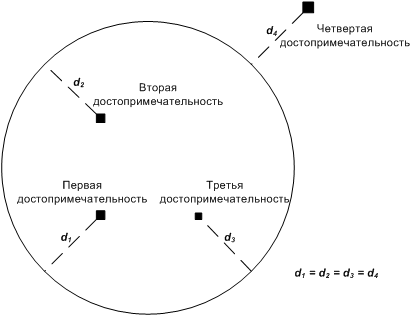
48: Кольцевая автодорога
К 2110 году город Флэтбург, являясь одним из крупнейших городов мира, не имеет обходной автомагистрали, что является существенным препятствием для его развития как крупнейшего транспортного центра мирового значения. В связи с этим ещё в 2065 году при разработке Генерального плана развития Флэтбурга была определена необходимость строительства кольцевой автомобильной дороги.
В Генеральном плане также были обозначены требования к этой дороге. Она должна соответствовать статусу кольцевой — иметь форму окружности. Кроме этого, четыре крупные достопримечательности Флэтбурга должны быть в одинаковой транспортной доступности от дороги. Это предполагается обеспечить тем, что они будут находиться на равном расстоянии от неё. Расстоянием от точки расположения достопримечательности до дороги называется наименьшее из расстояний от этой точки до некоторой точки, принадлежащей окружности автодороги.
Дирекция по строительству города Флэтбурга, ответственная за постройку кольцевой автодороги, решила привлечь передовых программистов для выбора оптимального плана постройки дороги.
Требуется написать программу, которая вычислит число возможных планов постройки кольцевой автомобильной дороги с соблюдением указанных требований и найдёт такой план, для которого длина дороги будет минимальной. Гарантируется, что хотя бы один план постройки существует.
Программа получает на вход четыре строки. Каждая из них содержит по два целых числа: $x_i$ и $y_i$ — координаты места расположения достопримечательности. Никакие две достопримечательности не находятся в одной точке.
Все числа не превосходят 100 по абсолютной величине.
В первой строке требуется вывести число возможных планов постройки кольцевой автомобильной дороги. Если таких планов бесконечно много, необходимо вывести в первой строке выходного файла слово Infinity .
Видео:ООП 28 Наследование. Расширение класса в Python. Extending python class in PythonСкачать

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2
Вступление
Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.
Начнем с взаимного расположения точки относительно прямой, луча и отрезка.
Задача №1
Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.
Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P1(x1, y1), P2(x2, y2). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P1P2 и P1M и по его знаку сделать вывод.
Задача №2
Определить принадлежит ли точка лучу.
Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P1(x1, y1) — начало луча, а P2(x2, y2) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P1(x1, y1), где P2(x2, y2) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (P1P2, P1M) ≥ 0 – скалярное произведение (точка лежит на луче)
Задача №3
Определить принадлежит ли точка отрезку.
Решение
Пусть точки P1(x1, y1), P2(x2, y2) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P1, P2. Далее нам нужно определить лежит ли точка между точками P1 и P2, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP1, MP2). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P1(x1, y1), P2(x2, y2) необходимо и достаточно выполнения условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (MP1,MP2) ≤ 0 – скалярное произведение (точка лежит между P1 и P2)
Задача №4
Взаимное расположение двух точек относительно прямой.
Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.
Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P1P2, P1M1] * [P1P2, P1M2] 0 – точки лежат по одну сторону.
3. [P1P2, P1M1] * [P1P2, P1M2] = 0 – одна (или две) из точек лежит на прямой.
Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P1P2, P1M1] * [P1P2, P1M2] ≤ 0.
Задача №5
Определить пересекаются ли две прямые.
Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a1x + b1y + c1 = 0 и a2x + b2y + c2 = 0. Тогда условие параллельности прямых заключается в том, что a1b2 — a2b1 = 0.
Если же прямые заданы точками P1(x1, y1), P2(x2, y2), M1(x3, y3), M2(x4, y4), то условие их параллельности заключается в проверки косого произведения векторов P1P2 и M1M2: если оно равно нулю, то прямые параллельны.
В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b1, a1), (-b2, a2) которые называются направляющими векторами.
Задача №6
Определить пересекаются ли два отрезка.
Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:
Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P1P2, P1M2] > 0, [P1P2, P1M1] [P1P2, P1M2] * [P1P2, P1M1] 2 + b 2 ).
Задача №8
Расстояние от точки до луча.
Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.
В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.
Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP1P2 – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
1. (P1M, P1P2) 2 .
Теперь рассмотрим случай, когда центр второго круга O2 находится между точками O1 и C. В этом случае получим отрицательное значение величины d2. Использование отрицательного значения d2 приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.
Заключение
Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.
🎬 Видео
#11. Слияние двух упорядоченных списков | Алгоритмы на PythonСкачать

Python. Вложенный цикл forСкачать

взаимное расположение двух окружностей.(не пересекаются)Скачать

Слияние списков. Метод двух указателей PythonСкачать

Пересечение списков. Совпадающие элементы двух списков. Решение задачи на Python.Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Функции trunc, floor, ceil. Округление вверх и вниз в pythonСкачать

Математика это не ИсламСкачать

15 Задача: Вычислить площадь и длину окружности круга при помощи PythonСкачать

Python с нуля. Урок 18 | Вложенные функции, замыканияСкачать

Python с нуля | Функции в Python | Определение, вызов, позиционные и именованные аргументы, returnСкачать