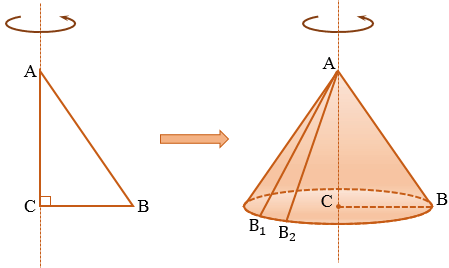
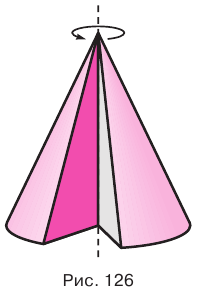
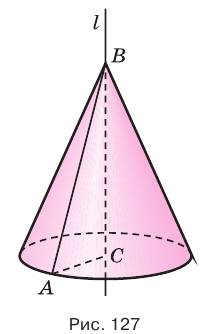
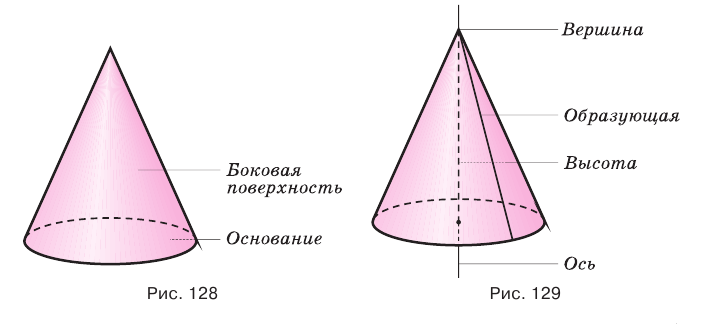
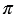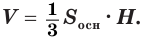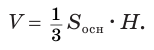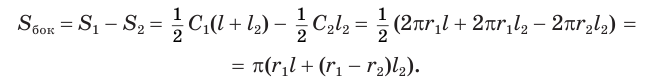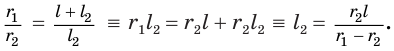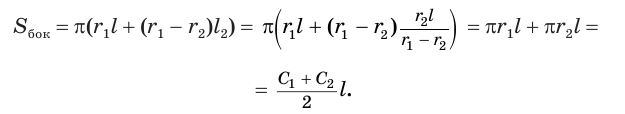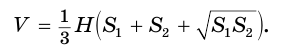Конус — это объемное тело, которое получается при вращении прямоугольного треугольника вокруг одного из его катетов.
Возьмем прямоугольный треугольник АВС. Будем вращать этот треугольник вокруг катета АС.
Прямая АС — ось косинуса.
Отрезок АС — высота конуса.
Основание конуса — круг, образованный при вращении катета ВС.
Коническая поверхность (или боковая поверхность конуса) — поверхность, образованная при вращении гипотенузы АВ и состоящая из отрезков с общим концом А.
Образующие конуса — отрезки, из которых составлена боковая поверхность конуса (на рисунке выше указаны образующие АВ, АВ1 и АВ2).
- Определение
- Объем конуса
- Доказательство
- Площадь боковой поверхности конуса
- Конус в геометрии — элементы, формулы, свойства с примерами
- Конус получен вращением прямоугольного треугольника вокруг одного из катетов. боковая поверхнос ть -тело, ограниченное конической поверхностью и кругом. — презентация
- Похожие презентации
- Презентация на тему: » Конус получен вращением прямоугольного треугольника вокруг одного из катетов. боковая поверхнос ть -тело, ограниченное конической поверхностью и кругом.» — Транскрипт:
- 💥 Видео
Определение
| Конус — это тело, ограниченное кругом и конической поверхностью. |
Объем конуса
| Объем конуса равен одной трети произведения площади основания на высоту. |
Доказательство
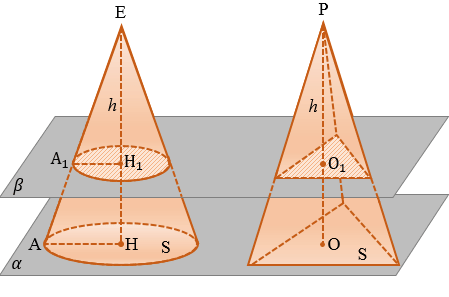
Дано: конус с площадью основания S, высотой h и объемом V.
Доказать: V = 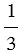
Доказательство:
Воспользуемся принципом Кавальери. Рассмотрим конус и пирамиду с площадями оснований S и высотами ЕН = h и РО = h соответственно, «стоящие» на одной плоскости 
Проведем секущую плоскость 

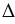
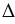
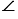
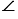
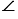

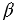
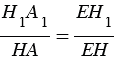
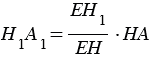
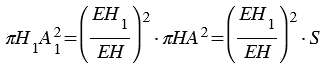
Площадь сечения пирамиды равна 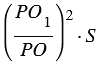
Следовательно, площадь сечения конуса равна площади сечения пирамиды. Поэтому и его объем равен объему пирамиды, т.е. V = 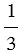
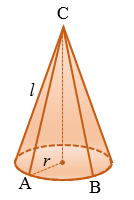
Площадь боковой поверхности конуса
Рассмотрим конус с радиусом основания 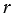
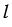
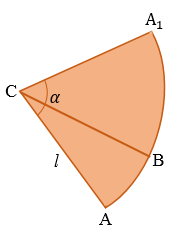
Представим, что его боковую поверхность разрезали по одной из образующих и развернули так, что получился круговой сектор.
Радиус этого сектора равен образующей конуса, т.е. равен 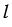
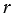

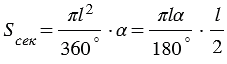
Длина дуги окружности с градусной мерой 
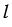
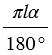
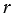
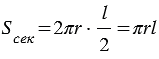
Площадь боковой поверхности конуса равна площади ее развертки, т.е. 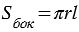 . . |
Поделись с друзьями в социальных сетях:
Видео:Геометрия 11 класс (Урок№7 - Конус.)Скачать

Конус в геометрии — элементы, формулы, свойства с примерами
Конусом называется тело, полученное вращением прямоугольного треугольника вокруг оси, проходящей через один из его катетов (рис. 126).
На рисунке 127 показано образование конуса при вращении прямоугольного треугольника 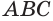
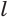
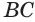
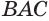
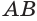
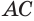
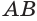
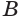
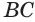
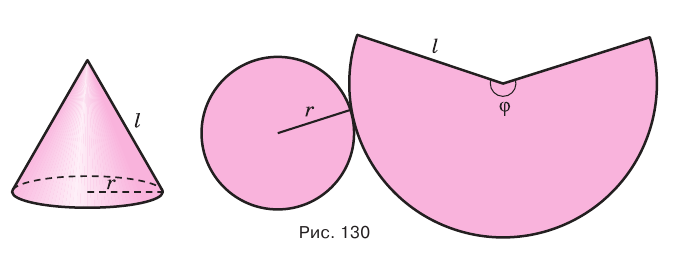
Поверхность конуса можно развернуть на плоскость, в результате получится сектор, представляющий боковую поверхность конуса, и круг, представляющий основание конуса. На рисунке 130 представлены конус и его развертка.
Теорема 5.
Боковая поверхность конуса равна произведению полуокружности его основания и образующей:
Доказательство проведите самостоятельно, используя рисунок 130.
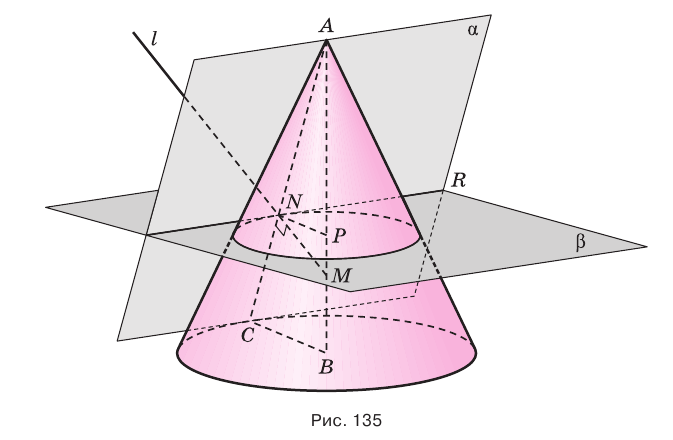
Важной пространственной конфигурацией, которая часто встречается в задачах, является сочетание конуса с плоскостью.
Если конус пересечь плоскостью, параллельной основанию, то получится круг (рис. 131), а если плоскостью, проходящей через вершину, то — равнобедренный треугольник, у которого боковые стороны являются образующими конуса (рис. 132).
Осевое сечение конуса, т. е. сечение плоскостью, проходящей через ось конуса, является равнобедренным треугольником, у которого основание равно диаметру основания конуса (рис. 133).
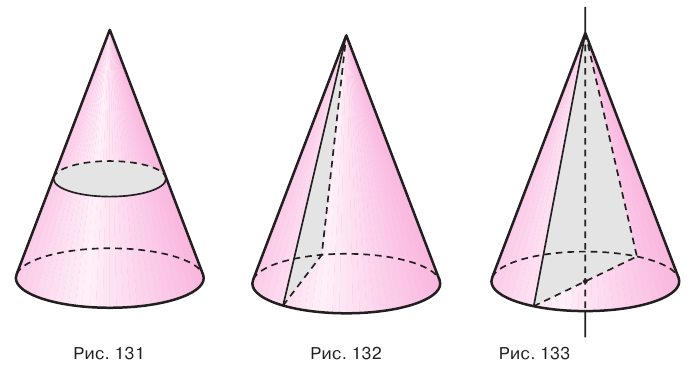
Проведем через вершину конуса секущую плоскость и будем ее поворачивать вокруг прямой, перпендикулярной оси конуса (рис. 134). При этом основание треугольника-сечения будет укорачиваться, а его боковые стороны сближаться до того момента, пока не совпадут. Получим плоскость, целиком содержащую образующую и не имеющую с конусом других общих точек. Такая плоскость называется касательной плоскостью конуса.
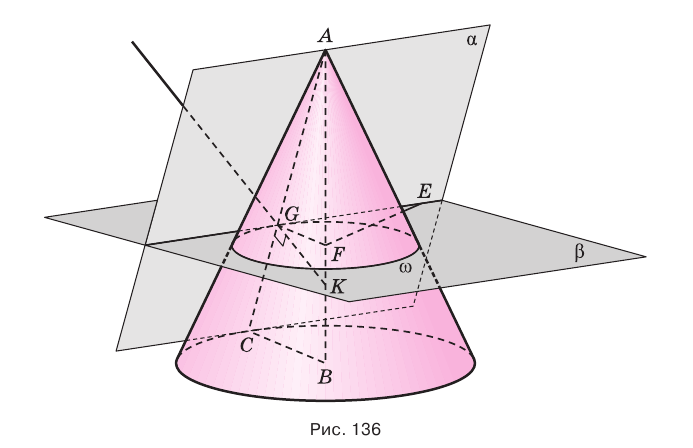
Теорема 6.
Если плоскость касается конуса по некоторой образующей, то ей перпендикулярна плоскость, проходящая через эту образующую и ось конуса.
Доказательство:
Пусть плоскость 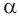

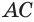

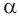
Проведем прямую 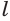

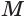
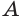
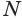
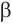

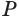
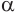
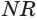
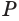
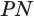
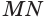
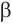
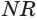
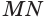
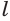
Таким образом, прямая 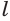

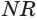
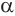
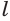

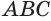
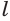

Теорема 6 выражает свойство касательной плоскости конуса.
Теорема 7.
Плоскость касается конуса, если она проходит через его образующую и перпендикулярна плоскости, проходящей через эту образующую и ось конуса.
Доказательство:
Пусть плоскость 


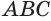



Точки образующей 



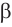

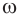
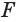

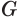

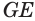
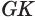


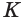
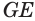
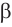
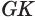
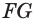
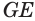
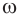
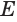
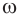
Теорема 7 выражает признак касательной плоскости конуса.
Пусть есть конус с вершиной 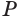
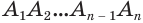
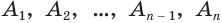
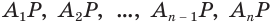
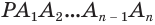
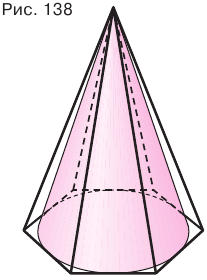
Если основание конуса вписано в основание пирамиды, а боковая поверхность конуса касается боковых граней пирамиды, то говорят, что пирамида описана около конуса, или конус вписан в пирамиду (рис. 138).
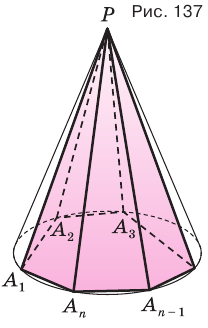
Теорема 8.
Объем конуса равен третьей доле произведения площади Рис. 139 т его основания и высоты:
Доказательство:
Пусть есть конус с осью 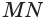
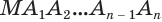
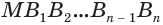
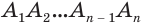
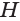
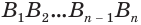
Будем увеличивать количество 
В описанном процессе высота 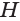
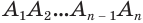
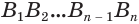
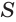
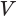
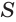
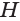
Теорема 9.
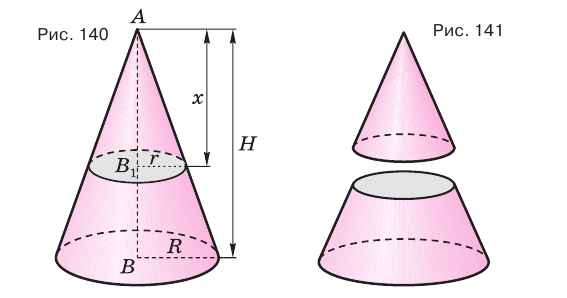
Если конус пересечь плоскостью, параллельной его основанию, то:
- а) образующая и высота разделяются на пропорциональные части;
- б) площади сечения и основания относятся как квадраты их расстояний от вершины.
Используя рисунок 140, докажите эту теорему самостоятельно.
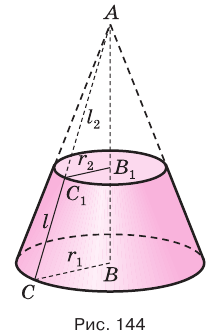
Секущая плоскость, параллельная основанию конуса, разделяет его на две части (рис. 141). Одна из этих частей также является конусом, а другая — телом, которое называется усеченным конусом.
Основание данного конуса и круг, полученный в сечении, называют основаниями усеченного конуса, а отрезок образующей данного конуса, заключенный между его основанием и секущей плоскостью, — образующей усеченного конуса (рис. 142). Высотой усеченного конуса называется перпендикуляр, проведенный из какой-либо точки одного его основания к плоскости другого основания.
Усеченный конус можно получить вращением прямоугольной трапеции вокруг боковой стороны, к которой прилежат прямые углы (рис. 143).
Пример:
Найдем боковую поверхность усеченного конуса. Пусть есть усеченный конус, у которого радиусы оснований 
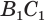
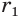
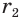
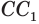
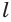
Достроим его до полного конуса. Достроенная часть представляет собой конус, у которого радиус основания равен 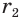
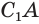
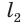
Боковую поверхность 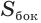
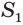
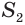
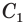
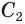
Найдем 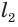
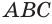
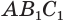
Таким образом, боковая поверхность усеченного конуса равна произведению полусуммы длин окружностей его оснований и образующей.
Пример:
Используя рисунок 144, можно, как и для усеченной пирамиды (см. параграф 9), доказать, что объем 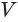
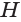
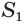
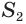
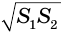
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Сфера в геометрии
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Возникновение геометрии
- Призма в геометрии
- Цилиндр в геометрии
- Пирамида в геометрии
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Конус путем вращения треугольникаСкачать

Конус получен вращением прямоугольного треугольника вокруг одного из катетов. боковая поверхнос ть -тело, ограниченное конической поверхностью и кругом. — презентация
Презентация была опубликована 9 лет назад пользователемart.ioso.ru
Похожие презентации
Видео:Конус. 11 класс.Скачать

Презентация на тему: » Конус получен вращением прямоугольного треугольника вокруг одного из катетов. боковая поверхнос ть -тело, ограниченное конической поверхностью и кругом.» — Транскрипт:
2 Конус получен вращением прямоугольного треугольника вокруг одного из катетов. боковая поверхнос ть -тело, ограниченное конической поверхностью и кругом. Коническая поверхность – поверхность, образованная отрезками, соединяющими т. P с каждой точкой окружности. Образующи е основание конуса ось конуса вершина конуса — это отрезки, которыми образована коническая поверхность — это коническая поверхность конуса — основанием является круг. является его высотой К О Н У СК О Н У С
3 За площадь боковой поверхности конуса принимается площадь её развертки. S бок = (πl 2 /360)*α S бок = π*r*l S кон =πr(l+ r) Площадь боковой поверхности конуса равна произведению половины длины окружности основания на высоту. полной поверхности Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания: S кон =πr(l+r)
4 Сечение плоскостью, параллельной оси Сечение плоскостью, параллельной основанию Сечение – круг с центром в т. О 1 Осевое сечение А B P APB AP=PB AB=d (Плоскость сечения проходит через ось конуса)
5 Площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую. S бок = π(r+r 1 )l Может быть получен вращением прямоугольной трапеции вокруг её боковой стороны, перпендикулярной к основаниям.
6 O1O1 M1M1 A A1A1 M r O L L1L1 α β образующие Образование цилиндрической поверхности. Рассмотрим две параллельные плоскости α и β и окр. L с центром О радиуса r, расположенную в пл. α. Через каждую точку окружности L проведём прямую, перпендикулярную к пл. α. Отрезки этих прямых, заключённые между плоскостями, образуют цилиндрическую поверхность. Отрезки АА 1, ММ 1 называются образующими цилиндрической поверхности. Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и L 1, называется ЦИЛИНДРОМ. боковой поверхностью цилиндра основаниями цилиндра образующими цилиндра осью цилиндра Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги — основаниями цилиндра. Образующими цилиндрической поверхности называются образующими цилиндра, прямая ОО 1 – осью цилиндра. Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон.
7 За площадь боковой поверхности цилиндра принимают площадь её развертки Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра. Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. П Л О Щ А Д Ь П О В Е Р Х Н О С Т И Ц И Л И Н Д Р А S бок =2πrh Sцил=2 πr(r+h)
8 С Е Ч Е Н И Я Ц И Л И Н Д Р А Осевое Секущая плоскость проходит через ось цилиндра, в сечении прямоугольник Сечение плоскостью, перпендикулярной к оси, в сечении круг.
9 ПРИМЕРЫ ЗАДАЧ С РЕШЕНИЯМИ ПО ТЕМЕ « СЕЧЕНИЕ КОНУСА И ЦИЛИНДРА » Задача 1. Высота цилиндра равна 12см, а радиус основания равен 10 см. Цилиндр пересечён плоскостью, параллельной оси, так, что в сечении получился квадрат. Найти расстояние от оси цилиндра до секущей плоскости. Решение: По условию задачи r=10, а h=12. Для нахождения расстояния от оси до плоскости сечения нужно найти величину расстояния ОН. Отрезок ОН перпендикулярен к стороне квадрата АВ, которая равна12см. ОА и ОВ равны радиусу основания r=10см. Δ ОАВ равнобедренный, ОН делит сторону АВ пополам. Таким образом, задача сводится к нахождению катета в прямоугольном треугольнике ОНА, который будет равен, по теореме Пифагора, квадратному корню из ( )=8. О А В С D Н Задача 2. Площадь осевого сечения конуса равна 0,6 см 2. Высота конуса равна 1,2 см. Вычислите площадь полной поверхности конуса. Решение: Формула нахождения площади полной поверхности конуса равна Sкон=πr(l+r) (1). В осевом сечении конуса получается треугольник, у которого основание равно 2r, высота h=1,2см и площадь S=0,6 см 2. Из формулы площади треугольника S=1/2*2r*h (2r-основание треугольника) находим r=0,5. Зная катет треугольника АВО, равный r, и гипотенузу, равную h, можем найти второй катет, равный l. По теореме Пифагора он равен корню квадратному из (1,2 2 +0,5 2 )=1,3. Теперь, зная все составляющие величины формулы (1), подставив, получаем S= π*05*(1,3+0,5)=0,9 π. l А В Оr
10 А эти задачки попробуй решить сам Задача 3. Высота цилиндра на 12см больше его радиуса, а площадь полной поверхности равна 288 π см 2. Найдите радиус основания и высоту цилиндра. Возможно, этот чертёж поможет тебе при решении. Задача 4. Осевое сечение конуса — правильный треугольник со стороной 2r. Найдите площадь сечения, проведённого через две образующих конуса, угол между которыми равен: а) 30 о, б) 45 о, в) 60 о. Посмотри на рисунок, и он поможет тебе решить задачу. l А В Оr 2r2r С И последняя Задача 4. Найдите образующую усечённого конуса, если радиусы оснований равны 3см и 6 см, а высота равна 4см. Чертёж усечённого конуса, приведённый здесь, наведёт тебя на правильные мысли. Удачи!
💥 Видео
Конус. Практическая часть. 11 класс.Скачать

Конус. Урок 8. Геометрия 11 классСкачать

Геометрия 9 класс (Урок№34 - Тела и поверхности вращения.)Скачать

9 класс, 42 урок, КонусСкачать

Решение задач на конусСкачать

Задание 5. ЕГЭ профиль. КОНУС.Скачать

Как найти объем. Принцип Кавальери | Ботай со мной #050 | Борис Трушин |Скачать

Понятие конуса. Видеоурок по геометрии 11 классСкачать

Длина окружности. Площадь круга. 6 класс.Скачать

Урок 19. Задачи на тела вращения из ЕГЭ. Цилиндр, конус, сфера. Стереометрия с нуля.Скачать

Геометрия. 11 класс. Конус и его элементы. Развертка, площадь боковой и полной поверхности конусаСкачать

Как сделать конус из листа бумаги, ватмана или картона своими руками. Поделки. Колпак.Скачать

Геометрия. 11 класс. Конус и его элементы. Развертка, площадь боковой и полной поверхности конусаСкачать

№550. Осевое сечение конуса — прямоугольный треугольник. Найдите площадь этого сечения, еслиСкачать

Построение натуральной величины треугольника методом вращенияСкачать

Способ вращения. Определение истинной величины отрезка.Скачать

Усеченный конус. 11 класс.Скачать