Высота треугольника разбивает его основание на два отрезка с длинами 8 и 9. Найдите длину этой высоты, если известно, что другая высота треугольника делит ее пополам.
Решение: 
Пусть BH — высота.
AH=8 и CH=9
Высота AL пересекает высоту BH в точке K:
BK=KH=x
Треугольники ∆AKH, ∆BLK и ∆BCH подобные.
Они прямоугольные в ∆AKH, ∆BLK т.к. углы AKH и BKL равны как вертикальные,
а ∆BLK, ∆BCH имеют общий угол B.
KH/AH=CH/BH
x/8=9/2x
x•2x=9•8
2x 2 =72
x 2 =36
x=6
Видео вебинара, где рассмотрено решение этой задачи и не только.
Кликните СЮДА, чтобы посмотреть видео.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Видео:Геометрия Высота треугольника разбивает его основание на два отрезка с длинами 8 и 9. Найдите длинуСкачать

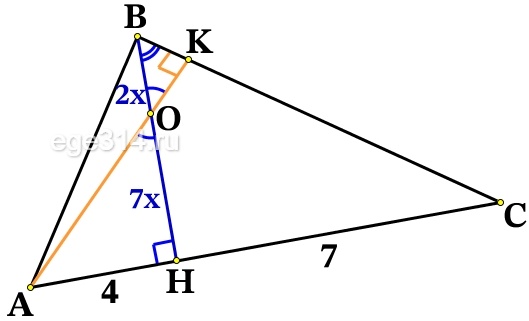
Решение №2547 Высота треугольника разбивает его основание на два отрезка с длинами 4 и 7.
Высота треугольника разбивает его основание на два отрезка с длинами 4 и 7. Найдите длину этой высоты, если известно, что другая высота треугольника делит её в отношении 2:7, считая от вершины.
Источник: ОГЭ Лысенко 2022 (40 вар)
Высота ВН делит основание АС на АН = 4 и НС = 7.
Высота АК делит высоту ВН на ВО = 2х и ОН = 7х, тогда ВН = 2х + 7х = 9х.
ΔАНО подобен ΔВКО, т.к. ∠АНО = ∠ВКО = 90°, ∠АОН = ∠ВОК как вертикальный. Запишем отношение пропорциональных сторон треугольников:
ΔBHC подобен ΔВКО, т.к. ∠BHC = ∠ВКО = 90°, ∠B – общий. Запишем отношение пропорциональных сторон треугольников:
В каждой пропорции возьмём последние две дроби и выразим из них KO:
Приравняем значения КО:
|: 7BK
x·9x = 4
9x 2 = 4
x 2 =
Зная х найдём искомую высоту ВН :
ВН = 9х = = 3·2 = 6
Видео:КАК НАЙТИ ВЫСОТУ ТРЕУГОЛЬНИКА? ЕГЭ и ОГЭ #shorts #егэ #огэ #математика #профильныйегэ #треугольникСкачать

Высота треугольника разбивает его основание на два отрезка с длинами 8
Высота треугольника разбивает его основание на два отрезка с длинами 8 и 9. Найдите длину этой высоты, если известно, что другая высота треугольника делит ее пополам. Пусть высота BH треугольника ABC разбивает основание AC на отрезки AH=8 и CH=9, высота AK пересекает высоту BH в точке M, причем BM=MH=x. Треугольники AHM и BKM подобны (по двум углам) Треугольники BKM и BHC подобны (по двум углам) Получаем пропорцию Следовательно, BM=6, и BH=12. Ответ: 12.
Слайд 29 из презентации «Признаки подобия треугольников»
Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Признаки подобия треугольников.pptx» можно в zip-архиве размером 5892 КБ.
Видео:№955. Высота треугольника, равная 10 см, делит основание на два отрезка, равные 10 см и 4 см.НайдитеСкачать

Подобие треугольников
«Три признака подобия треугольников» — Отрезки. Разминка. Первый признак подобия треугольников. Треугольники KPF и ЕМТ подобны. Найдите площадь треугольника. Общий множитель. Второй признак подобия треугольников. Углы треугольников соответственно равны. Параллелограмм. Отношение площадей двух квадратов. Отрезок. Отношение площадей. Пропорциональность отрезков.
«Применение подобия» — В каком отношении данная высота делит площадь треугольника? Применение подобия к решению задач. Найдите периметр ABCD. Наибольшее количество баллов 13. Проговор. 1 вариант Определение подобных треугольников. Отметки. 7. В равнобедренной трапеции диагональ делит острый угол пополам. 4. Биссектриса прямого угла разделила гипотенузу на отрезки 6 см и 8 см.
«Применение подобия треугольников» — Задачи на построение. Свойство медиан треугольника. Определение высоты предмета с помощью зеркала. Построение треугольников. Определение расстояния до недоступной точки. Измерительные работы на местности. Практическое применение подобия треугольников. Определение высоты предмета. Пропорциональные отрезки в прямоугольном треугольнике.
«Урок Признаки подобия треугольников» — В подобных фигурах углы равны. Когда. Подобные фигуры. Треугольники подобны? Третий признак подобия треугольников. Задачи урока: Если две стороны одного треугольника пропорциональны двум сторонам другого. Цель урока: Обобщение по теме «Признаки подобия треугольников». Урок геометрии «Признаки подобия треугольников».
«Задачи на подобие» — Пример № 6. Пример № 7. Пример № 5. Пример № 4. Пример № 3. Второй и третий признаки подобия треугольников. Пример № 1. Первый признак подобия треугольников. Подобные треугольники. Темы задач. Пример № 2. Решение задач по геометрии на готовых чертежах.
«Признаки подобия» — Признаки подобия треугольников. Дано: ?АВС, ?А1В1С1 AB/A1B1=BC/B1C1=CA/C1A1. Подобные треугольники. Доказательство теоремы. Определение подобных треугольников. Итак, стороны треугольника АВС пропорциональны сходственным сторонам треугольника А1В1С1. Второй признак подобия треугольников. Дано. 13. Первый признак подобия треугольников.
Всего в теме «Подобие треугольников» 23 презентации
🔥 Видео
огэ 2часть планиметрияСкачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

№110. Докажите, что если медиана треугольника совпадает с его высотой, то треугольникСкачать

Свойство биссектрисы треугольника с доказательствомСкачать

№488. Найдите: а) высоту равностороннего треугольника, если его сторона равна 6 см;Скачать

Площади треугольников с равным углом.Скачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Задача, которую исключили из экзамена в АмерикеСкачать

НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать

Геометрия В треугольнике проведены три медианы. Докажите, что они разбивают треугольник на шестьСкачать

Геометрия Средняя линия равностороннего треугольника со стороной 6 см разбивает его на треугольник иСкачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Решаем геометрию ОГЭ по математике 2024! Задание №15.Скачать

Высота в прямоугольном треугольнике. 8 класс.Скачать