- Окружность построена на медиане треугольника
- Как построить медиану окружности
- Медиана треугольника
- Как начертить медиану и высоту треугольника с помощью циркуля ?
- Задачи на построение циркулем и линейкой с примерами решения
- Задача 1 (построение угла, равного данному)
- Задача 2 (построение серединного перпендикуляра к отрезку)
- Задача 3 (построение биссектрисы угла)
- Построение треугольника по трем элементам
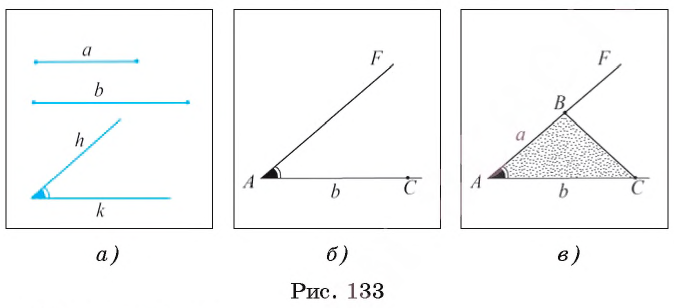
- Задача 4 (построение треугольника по двум сторонам и углу между ними)
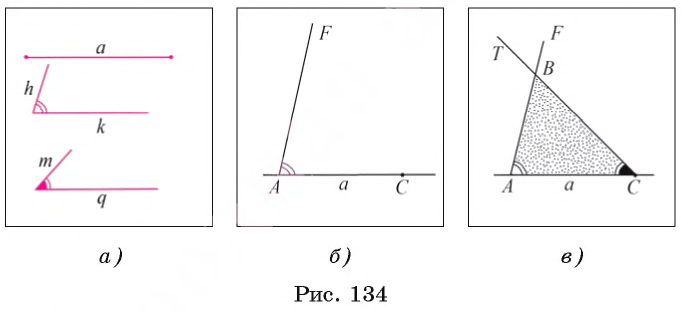
- Задача 5 (построение треугольника по стороне и двум прилежащим к ней углам)
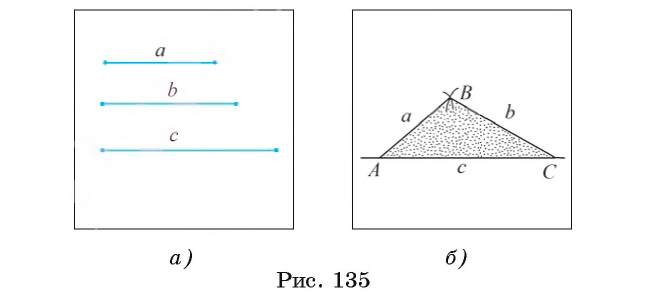
- Задача 6 (построение треугольника по трем сторонам)
- Определение и свойства медианы треугольника
- Определение медианы треугольника
- Свойства медианы
- Свойство 1 (основное)
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Примеры задач
- Олимпиадные задания по математике 8 — 11 класс
- Олимпиадные задания по математике 8 — 11 класс
- Олимпиадные задания по математике 8 класс
- Олимпиадные задания по математике 8 класс
- Олимпиадные задания по математике 9 класс
- Олимпиадные задания по математике 9 класс
- Олимпиадные задания по математике 9 класс
- Олимпиадные задания по математике 10 класс
- Олимпиадные задания по математике 10 класс
- Олимпиадные задания по математике 11 класс
- Олимпиадные задания по математике 11 класс
- Свойства медианы треугольника. Итоговое повторение курса геометрии 7 – 9 класса
Видео:11.49.1. Планиметрия. Гордин Р.К.Скачать

Окружность построена на медиане треугольника
Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K.
а) Докажите, что отрезок BK втрое больше отрезка CK.
б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 18 и BN = 17.
а) Проведём медиану AE к основанию BC, поскольку треугольник ABC — равнобедренный, медиана AE является биссектрисой и высотой. Проведём MK, заметим, что ∠BKM = 90°, так как он вписанный и опирается на диаметр окружности. Поэтому MK перпендикуляр к ВС. Тогда MK — средняя линия AEС, и тогда КС = EК. Поскольку CE = 2CK, имеем: BK = 3CK, что и требовалось доказать.
б) Заметим, что ∠BKM = ∠BNM = 90°, так как эти углы вписанные и опираются на диаметр. Тогда (*), причём:
Подставляя полученные соотношения в (*), получаем:
Тогда
Приведём другое решение пункта б).
Пусть Тогда
и пусть
тогда
По свойству секущих имеем:
Приведём третье решение пункта б).
Пусть угол при вершине A треугольника ABC равен 2α, AB = x. Тогда из прямоугольного треугольника ANM находим: Из треугольника MKC:
таким образом, получаем уравнение:
Из последнего уравнения получаем те же ответы, что и в предыдущем решении x = 16 (постороннее решение) или x = 18.
Приведём еще одно решение пункта б).
Рассмотрим прямоугольный треугольник Если AB = x, то
С другой стороны из треугольника ABC по теореме косинусов имеем
Составим уравнение:
Последнее уравнение уже дважды решено выше.
| Критерии оценивания выполнения задания | Баллы | ||
|---|---|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 | ||
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 | ||
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать  Как построить медиану окружностиВидео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать  Медиана треугольникаЧто называется медианой треугольника? Определение. Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Как построить медиану треугольника? Чтобы построить медиану треугольника , надо: 1) С помощью линейки найти и отметить середину стороны треугольника. 2) Соединить полученную точку с вершиной, лежащей напротив этой стороны. Рисунок медианы треугольника: Как построить медиану треугольника с помощью циркуля и линейки без шкалы, мы рассмотрим позже, в теме «Построить треугольник». Сколько медиан имеет треугольник? Так как у треугольника три вершины и три стороны, то и отрезков, соединяющих вершину и середину противолежащей стороны, тоже три. Значит, треугольник имеет три медианы. Все три медианы треугольника пересекаются в одной точке: Точка пересечения медиан называется центром тяжести треугольника. В точке пересечения медианы треугольника делятся в отношении два к одному, считая от вершины: Об этом свойстве медиан треугольника, а также о том, как найти длину медианы через длины сторон треугольника, более подробно мы поговорим позже и рассмотрим, как свойства медианы использовать при решении задач. Кроме того, отдельно будут рассмотрены медиана прямоугольного треугольника, проведенная к гипотенузе и медиана равнобедренного треугольника, проведенная к его основанию, поскольку каждая из них обладает своими свойствами, которые надо знать и уметь применять. Видео:Задача 16. (Планиметрия) Математика профильСкачать  Как начертить медиану и высоту треугольника с помощью циркуля ?Постройте треугольник ABC. Пусть необходимо провести медиану из вершины С к стороне AB. Найдем середину стороны AB. Установите иглу циркуля в точке A. Другой конец циркуля поставьте в точку B. Тем самым ножками циркуля вы отмерили длину AB. Проведите окружность с центром в точке A и радиусом R, равным AB. Затем, не меняя расстояния между ножкам циркуля, установите иглу циркуля в точке B. Проведите окружность с центром в точке В и тем же радиусом AB. Окружности, проведенные из точек А и В, должны пересечься в двух точках. Назовите их, например, М и Т. Соедините линейкой точки М и Т. Точка, в которой отрезок МТ пересечет отрезок АВ, и будет являться серединой отрезка АВ. Назовем эту точку точкой Е. Кстати, прямая МТ будет не только делить отрезок АВ пополам, но и являться перпендикуляром к нему. Так что если перед вами стоит задача построить перпендикуляр к отрезку, действуйте по той же схеме, что и для нахождения середины отрезка. Итак, поскольку Е — середина стороны АВ, то отрезок СЕ будет являться искомой медианой треугольника, проведенной из вершины С к стороне АВ. Соедините при помощи линейки точки С и Е. Если необходимо провести также медианы из вершин треугольника А и В к сторонам ВС и АС соответственно, проделайте аналогичную процедуру. Помните, что все три медианы треугольника должны пересечься в одной точке. В стороне от чертежа описывайте свои действия. Последовательно отмечайте, что вы строите. Какие линии, окружности вы проводите, и какими буквами обозначаете точки, получаемые на пересечениях. В задачах на построение циркулем и линейкой обычно требуется не только построить что-либо, но и доказать, что используемая последовательность действий привела к нужному результату. По построению четырехугольник АМВТ является ромбом (АМ=ВМ=АТ=ВТ=AB). Ромб — частный случай параллелограмма. Диагонали параллелограмма точкой пересечения делятся пополам (свойство параллелограмма) . То есть, точка Е, полученная на пересечении диагоналей ромба АВ и МТ, дает середину АВ. Т. к. точка Е — середина АВ, то СЕ — медиана треугольника АВС (по определению) . Что и требовалось доказать. Вам надо определить ТОЧКУ, куда вести медиану и высоту? Или просто начертить? Начертить, так у циркуля с одной стороны остриё, а вот с другой карандаш (или рейсфедер) . Вот этим концом и чертите. А мединану надо определить среднюю сторону у противоположного угла. Циркулем произвольно чертите дуги с двух концов стороны, что бы они пересекались. И от противоположного угла проводите линию (медиану) с местам пересечения дуг (но до стороны треугольника, там и будет середина) . Высота прище. Делайте рисунок на листе в клетку. И от вершины вниз параллельно клеткам, т. е. перепендикулярно основанию треугольника. Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать  Задачи на построение циркулем и линейкой с примерами решенияСодержание: Основные задачи на построение циркулем и линейкой: В данном параграфе рассмотрим вопрос о построении геометрических фигур. Вы уже знаете, что геометрические построения можно осуществлять с помощью масштабной линейки, циркуля, транспортира и чертежного угольника. В то же время оказывается, что многие геометрические фигуры можно построить, пользуясь только циркулем и линейкой без масштабных делений. При построении геометрических фигур с помощью циркуля и линейки без масштабных делений учитывается, что:
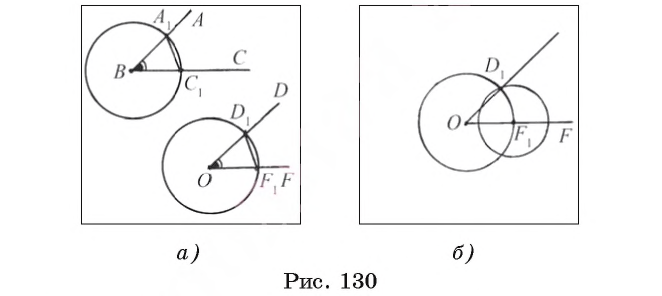
Теперь рассмотрим основные задачи на построение циркулем и линейкой: построение угла, равного данному, построение серединного перпендикуляра к отрезку, построение биссектрисы угла. Видео:Планиметрия_Треугольник_02Скачать  Задача 1 (построение угла, равного данному)От данного луча OF отложите угол, равный данному углу ABC. Предположим, что угол DOF, удовлетворяющий условию задачи, построен (рис. 130, а). Пусть 1) Строим окружность 2) Строим окружность 3) Строим окружность 4) Пусть D1 — одна из точек пересечения окружностей Равенство Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать  Задача 2 (построение серединного перпендикуляра к отрезку)Постройте серединный перпендикуляр к данному отрезку АВ. Проведем рассуждения, которые помогут осуществить необходимое построение. Предположим, что серединный перпендикуляр а к отрезку АВ построен (рис. 131, а). Пусть точки F и D лежат на серединном перпендикуляре так, что OF = OD. Прямоугольные треугольники FOB и DOB равны по двум катетам, следовательно, BF = BD. Иначе говоря, точки F и D лежат на окружности 1) Строим окружности 2) Отмечаем точки F и D пересечения окружностей 3) Тогда прямая FD — серединный перпендикуляр к отрезку АВ. Докажем это. Рассмотрим треугольники FAD и FBD (рис. 131, в). Указанные треугольники равны по трем сторонам. Следовательно, Видео:На катете ML прямоугольного треугольника KLM как на диаметре построена окружностьСкачать  Задача 3 (построение биссектрисы угла)Постройте биссектрису данного угла ABC. Допустим, что биссектриса BE данного угла ABC построена (рис. 132, а). Пусть точки F и D лежат на сторонах угла так, что BF = BD, О = FD 1) Строим окружность 2) Отмечаем точки F и D, в которых окружность 3) Строим окружности 4) Проводим луч ВТ. Луч ВТ — искомый. Докажем это. Рассмотрим треугольники BFT и BDT (рис. 132, в). Эти треугольники равны по трем сторонам (BF = BD и FT = DT — по построению, ВТ — общая сторона). Из равенства этих треугольников следует, что Видео:Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать  Построение треугольника по трем элементамВ данном пункте рассмотрим задачи на построение треугольника по: а) двум сторонам, и углу между ними; б) стороне и двум прилежащим к ней углам; в) трем сторонам. Видео:Олегу Тинькову запрещён вход на Мехмат МГУСкачать  Задача 4 (построение треугольника по двум сторонам и углу между ними)Постройте треугольник, две стороны которого равны двум данным отрезкам а и b, а угол между этими сторонами равен данному углу hk. Даны два отрезка а, b и угол hk (рис. 133, а). Требуется с помощью циркуля и линейки построить треугольник ABC, две стороны которого, например, АВ и АС, равны соответственно отрезкам а и b, а угол ВАС равен углу hk. 1) Проведем прямую, на ней отложим отрезок АС, равный отрезку b (рис. 133, б). 2) Строим угол CAF, равный углу hk. 3) На луче AF отложим отрезок АВ, равный отрезку а, и проведем отрезок ВС. Треугольник ABC — искомый (рис. 133, в). По построению имеем, что АС = b, АВ = а и При любых данных отрезках а и b и неразвернутом угле hk каждое из построений 1) — 3) выполнимо, т. е. искомый треугольник можно построить. Треугольники, которые удовлетворяют условию задачи и строятся при различном выборе прямой и отрезка АС, равны между собой по двум сторонам и углу между ними, поэтому говорят, что данная за дача имеет единственное решение. Видео:Окружность, построенная на стороне треугольника как на диаметреСкачать  Задача 5 (построение треугольника по стороне и двум прилежащим к ней углам)Постройте треугольник, сторона которого равна данному отрезку а, а углы, прилежащие к этой стороне, равны данным углам hk и mq. Дан отрезок а и два угла hk и mq (рис. 134, а). Требуется с помощью циркуля и линейки построить треугольник ABC, сторона которого, например АС, равна отрезку а, а углы ВАС и ВСА равны соответственно углам hk и mq. 1) Проведем прямую и на ней отложим с помощью циркуля отрезок АС, равный отрезку а (рис. 134, б). 2) Строим угол CAF, равный углу hk. 3) Строим угол ACT, равный углу mq. 4) Отмечаем точку В пересечения лучей AF и СТ. Треугольник ABC — искомый (рис. 134, в). По построению имеем, что АС = a, Для любого данного отрезка а и неразвернутых углов hk и mq каждое из построений 1) — 4) выполнимо, т. е. искомый треугольник можно построить. Треугольники, которые удовлетворяют условию задачи и строятся при различном выборе прямой и отрезка АС, равны между собой по стороне и двум прилежащим к ней углам, поэтому говорят, что данная задача имеет единственное решение. Видео:Построение угла, равного данному. 7 класс.Скачать  Задача 6 (построение треугольника по трем сторонам)Постройте треугольник, стороны которого равны данным отрезкам а, b, с. Даны отрезки а, b, с (рис. 135, а). Требуется с помощью циркуля и линейки построить треугольник ABC, стороны которого АВ, ВС и АС равны соответственно отрезкам a, b и с. 1) Проведем прямую и на ней с помощью циркуля отложим отрезок АС, равный отрезку с (рис. 135, б). 2) Строим окружность 3) Строим окружность 4) Пусть В — одна из точек пересечения окружностей По построению АС = с, АВ = а, ВС = b. Данная задача не всегда имеет решение. Известно, что в любом треугольнике длина каждой стороны меньше суммы длин двух других его сторон. Таким образом, если длина какого-либо из данных отрезков больше суммы длин двух других, то нельзя построить треугольник, стороны которого равны данным отрезкам.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи Сайт пишется, поддерживается и управляется коллективом преподавателей Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC. Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг. Видео:2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать  Определение и свойства медианы треугольникаВ данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала. Видео:№109. В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найдите медиану AMСкачать 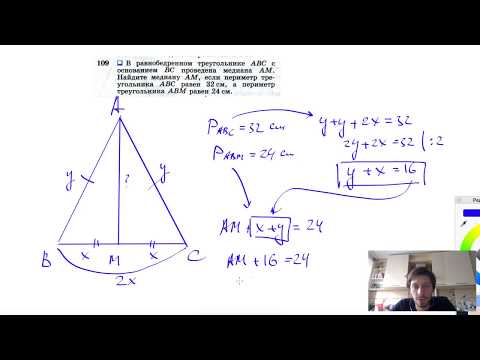 Определение медианы треугольникаМедиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины. Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F). Видео:№118. На основании ВС равнобедренного треугольника ABC отмечены точки М и N так, что BM=CN. ДокажитеСкачать 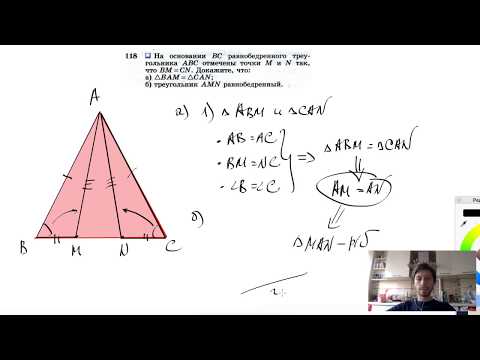 Свойства медианыСвойство 1 (основное)Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника. В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.: Свойство 2Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника. Свойство 3Три медианы делят треугольник на 6 равновеликих треугольников. Свойство 4Наименьшая медиана соответствует большей стороне треугольника, и наоборот.
Свойство 5Допустим, известны все стороны треугольника (примем их за a, b и c). Длину медианы ma, проведенную к стороне a, можно найти по формуле: Видео:Математика без Ху!ни. Функции нескольких переменных. Область определения. Линии уровня.Скачать  Примеры задачЗадание 1 Решение Задание 2 Решение Видео:✓ Все сюжеты по планиметрии из ЕГЭ за 50 минут | ЕГЭ. Задание 16. Профильный уровень | Борис ТрушинСкачать  Олимпиадные задания по математике 8 — 11 классВидео:Высота, биссектриса, медиана. 7 класс.Скачать  Олимпиадные задания по математике 8 — 11 классВидео:№119. В равнобедренном треугольнике DEK с основанием DK=16см отрезок EF— биссектриса,Скачать  Олимпиадные задания по математике 8 класс1. На доске была нарисована система координат и отмечены точки A(1;2) и B(3;1). Систему координат стерли. Восстановите ее по двум отмеченным точкам. 2. В некотором треугольнике биссектрисы двух внутренних углов продолжили до пересечения с описанной окружностью и получили две равные хорды. Верно ли, что треугольник равнобедренный? 3. В правильном шестиугольнике АВСDEF на прямой AF взята точка X так, что угол XСD = 45 o . Найдите угол FXE. 4. Около четырехугольника ABCD можно описать окружность. Точка p – основание перпендикуляра, опущенного из точки А на прямую ВС, Q – из А на DC, R – из D на АВ и Т – из D на ВС. Докажите, что точки p, Q, R и T лежат на одной окружности. 5. Восстановите остроугольный треугольник по ортоцентру и серединам двух сторон. 6. Противоположные стороны выпуклого шестиугольника ABCDEF параллельны. Назовем его «высотами» векторы с концами на прямых, содержащих противолежащие стороны, перпендикулярные им и направленные от AB к DE, от EF к BC и от CD к AF. Докажите, что вокруг этого шестиугольника можно описать окружность тогда и только тогда, когда сумма его «высот» равна нулевому вектору. Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать  Олимпиадные задания по математике 8 класс1. Биссектриса угла В и биссектриса внешнего угла D прямоугольника ABCD пересекают сторону AD и прямую АВ в точках М и К соответственно. Докажите, что отрезок МК равен и перпендикулярен диагонали прямоугольника. 2. В равнобедренном треугольнике АВС на боковой стороне ВС отмечена точка М так, что отрезок СМ равен высоте треугольника, проведенной к этой стороне, а на боковой стороне АВ отмечена точка К так, что угол КМС – прямой. Найдите угол АСК . 3. Из листа бумаги в клетку вырезали квадрат 2×2. Используя только линейку без делений и не выходя за пределы квадрата, разделите диагональ квадрата на 6 равных частей. 4. В трапеции ABCD : AB = BC = CD , CH – высота. Докажите, что перпендикуляр, опущенный из Н на АС , проходит через середину BD . 5. Пусть AA 1 и BB 1 – высоты неравнобедренного остроугольного треугольника АВС , М – середина АВ . Окружности, описанные около треугольников AMA 1 и BMB 1 пересекают прямые АС и ВС в точках К и L соответственно. Докажите, что К , М и L лежат на одной прямой. 6. Один треугольник лежит внутри другого. Докажите, что хотя бы одна из двух наименьших сторон (из шести) является стороной внутреннего треугольника. Олимпиадные задания по математике 9 класс1. Постройте треугольник по стороне, противолежащему углу и медиане, проведенной к другой стороне ( исследование вопроса о количестве решений не требуется ). 2. В выпуклом четырехугольнике ABCD Ð ABC = 90 0 , Ð BAC = Ð CAD , AC = AD , DH — высота треугольника ACD . В каком отношении прямая BH делит отрезок CD ? 3. Внутри отрезка АС выбрана произвольная точка В и построены окружности с диаметрами АВ и ВС . На окружностях (в одной полуплоскости относительно АС ) выбраны соответственно точки M и L так, что Ð MBA = Ð LBC . Точки K и F отмечены соответственно на лучах ВМ и BL так, что BK = BC и BF = AB . Докажите, что точки M , K , F и L лежат на одной окружности. 4. В треугольнике ABC M — точка пересечения медиан, O — центр вписанной окружности, A’ , B’ , C’ — точки ее касания со сторонами BC , CA , AB соответственно. Докажите, что, если CA’ = AB , то прямые OM и AB перпендикулярны. 5. Дан треугольник АВС . Точка О 1 — центр прямоугольника ВСDE , построенного так, что сторона DE прямоугольника содержит вершину А треугольника. Точки О 2 и О 3 являются центрами прямоугольников, построенных аналогичным образом на сторонах АС и АВ соответственно. Докажите, что прямые АО 1 , ВО 2 и СО 3 пересекаются в одной точке. 6. На плоскости расположен круг. Какое наименьшее количество прямых надо провести, чтобы, симметрично отражая данный круг относительно этих прямых (в любом порядке конечное количество раз), можно было накрыть им любую заданную точку плоскости? Олимпиадные задания по математике 9 класс9.1. В выпуклом четырехугольнике АВС D Е – середина CD , F – середина А D , K – точка пересечения АС и ВЕ . Докажите, что площадь треугольника BKF в два раза меньше площади треугольника АВС . 9.2. Постройте треугольник АВС по углу А и медианам, проведенным из вершин В и С . 9.3. Дан квадрат ABCD . Найдите геометрическое место точек M таких, что Ð AMB = Ð CMD . 9.4. Треугольник ABC вписан в окружность. Через точки A и B проведены касательные к этой окружности, которые пересекаются в точке p . Точки X и Y – ортогональные проекции точки p на прямые AC и BC . Докажите, что прямая XY перпендикулярна медиане треугольника ABC , проведенной из вершины C . 9.5. Диагонали вписанного четырёхугольника ABCD пересекаются в точке M , Ð AMB = 60 ° . На сторонах AD и BC во внешнюю сторону построены равносторонние треугольники ADK и BCL . Прямая KL пересекает описанную около ABCD окружность в точках p и Q . Докажите, что pK = LQ . 9.6. Длина каждой стороны и каждой не главной диагонали выпуклого шестиугольника не превосходит 1. Докажите, что в этом шестиугольнике найдется главная диагональ, длина которой не превосходит 2 деленное на корень из 3 . Олимпиадные задания по математике 9 класс1. На рисунке изображен параллелограмм и отмечена точка p пересечения его диагоналей. Проведите через p прямую так, чтобы она разбила параллелограмм на две части, из которых можно сложить ромб. 2. Квадрат и прямоугольник одинакового периметра имеют общий угол. Докажите, что точка пересечения диагоналей прямоугольника лежит на диагонали квадрата. 4. Постройте треугольник по стороне, радиусу вписанной окружности и радиусу вневписанной окружности, касающейся этой стороны. (Исследование проводить не требуется.) 5. В некоторой точке круглого острова радиусом 1 км зарыт клад. На берегу острова стоит математик с прибором, который указывает направление на клад, когда расстояние до клада не превосходит 500 м. Кроме того, у математика есть карта острова, на которой он может фиксировать все свои перемещения, выполнять измерения и геометрические построения. Математик утверждает, что у него есть алгоритм, как добраться до клада, пройдя меньше 4 км. Может ли это быть правдой? 6. Фиксированы две окружности w1 и w2, одна их внешняя касательная l и одна их внутренняя касательная m. На прямой m выбирается точка X, а на прямой l строятся точки Y и Z так, что XY и XZ касаются w1 и w2 соответственно, а треугольник XYZ содержит окружности w1 и w2. Докажите, что центры окружностей, вписанных в треугольники XYZ , лежат на одной прямой. Олимпиадные задания по математике 10 класс10.1. Е и F – середины сторон ВС и AD выпуклого четырехугольника АВС D . Докажите, что отрезок EF делит диагонали АС и BD в одном и том же отношении. 10.2. Существует ли в пространстве замкнутая самопересекающаяся ломаная, которая пересекает каждое свое звено ровно один раз, причем в его середине? 10.3. На доске была нарисована окружность с отмеченным центром, вписанный в нее четырехугольник, и окружность, вписанная в него, также с отмеченным центром. Затем стерли четырехугольник (сохранив одну вершину) и вписанную окружность (сохранив ее центр). Восстановите какую-нибудь из стертых вершин четырехугольника, пользуясь только линейкой и проведя не более шести линий. 10.4. В треугольнике АВС : М – точка пересечения медиан, О – центр вписанной окружности. Докажите, что если прямая ОМ параллельна стороне ВС , то точка О равноудалена от сторон АВ и АС . 10.5. Трапеция АВС D с основаниями AB и CD вписана в окружность. Докажите, что четырехугольник, образованный ортогональными проекциями любой точки этой окружности на прямые AC , BC , AD и BD , является вписанным. 10.6. В тетраэдре DABC : Ð ACB = Ð ADB , ( С D ) ^ ( АВС ). В треугольнике АВС дана высота h , проведенная к стороне АВ , и расстояние d от центра описанной окружности до этой стороны. Найдите длину CD . Олимпиадные задания по математике 10 класс1. Каждый из двух подобных треугольников разрезали на два треугольника так, что одна из получившихся частей одного треугольника подобна одной из частей другого треугольника. Верно ли, что оставшиеся части также подобны? 2. Даны радиусы r и R двух непересекающихся окружностей. Общие внутренние касательные этих окружностей перпендикулярны. Найдите площадь треугольника, ограниченного этими касательными, а также общей внешней касательной. 3. Дан четырехугольник ABCD. A’, B’, C’ и D’ – середины сторон BC, CD, DA и AB соответственно. Известно, что AA’ = CC’ и BB’ = DD’. Верно ли, что ABCD параллелограмм? 4. В треугольнике АВС угол А равен 120 o . Докажите, что расстояние от центра описанной окружности до ортоцентра равно АВ + АС. 6. Есть два платка: один в форме квадрата, другой – в форме правильного треугольника, причем их периметры одинаковы. Существует ли многогранник, который можно полностью оклеить этими двумя платками без наложений (платки можно сгибать, но нельзя резать)? 6. Дан треугольник ABC и точки p и Q. Известно, что треугольники, образованные проекциями p и Q на стороны ABC, подобны (соответствуют друг другу вершины, лежащие на одних и тех же сторонах исходного треугольника). Докажите, что прямая pQ проходит через центр описанной окружности треугольника ABC. Олимпиадные задания по математике 11 класс1. AD и BE – высоты треугольника АВС . Оказалось, что точка C’ , симметричная вершине С относительно середины отрезка DE , лежит на стороне AB . Докажите, что АВ – касательная к окружности, описанной около треугольника DEC’ . 2. Прямая а пересекает плоскость α . Известно, что в этой плоскости найдутся 2011 прямых, равноудаленных от а и не пересекающих a. Верно ли, что а перпендикулярна α ? 3. Дана неравнобокая трапеция ABCD ( AB || CD ). Произвольная окружность, проходящая через точки А и В , пересекает боковые стороны трапеции в точках p и Q , а диагонали – в точках M и N . Докажите, что прямые pQ , MN и CD пересекаются в одной точке. 4. Докажите, что любой жесткий плоский треугольник T площади меньше четырёх можно просунуть сквозь треугольную дырку Q площади 3. 5. В выпуклом четырехугольнике ABCD : AC ⊥ BD , ∠ BCA = 10°, ∠ BDA = 20°, ∠ BAC = 40°. Найдите ∠ BDC . ( Ответ выразите в градусах. ) 6. Пусть AA 1, BB 1 и CC 1 – высоты неравнобедренного остроугольного треугольника АВС ; окружности, описанные около треугольников АВС и A 1 B 1 C , вторично пересекаются в точке Р , Z – точка пересечения касательных к описанной окружности треугольника АВС , проведённых в точках А и В . Докажите, что прямые АР , ВС и ZC 1 пересекаются в одной точке. Олимпиадные задания по математике 11 класс1. Существуют ли два таких четырехугольника, что стороны первого меньше соответствующих сторон второго, а соответствующие диагонали больше? 2. Трапеция ABCD и параллелограмм MBDK расположены так, что стороны параллелограмма параллельны диагоналям трапеции (см. рис.). Докажите, что площадь зеленой части равна сумме площадей синих частей. 3. В остроугольном треугольнике АВС проведены высоты АА1 и ВВ1. Докажите, что перпендикуляр, опущенный из точки касания вписанной окружности со стороной ВС на прямую АС, проходит через центр вписанной окружности треугольника А1СВ1. 4. На медианах треугольника как на диаметрах построены три окружности. Известно, что они попарно пересекаются. Пусть C1 — более удаленная от вершины C точка пересечения окружностей, построенных на медианах AM1 и BM2. Точки A1 и B1 определяются аналогично. Докажите, что прямые АА1, ВВ1 и СС1 пересекаются в одной точке. 5. Докажите, что у любого выпуклого многогранника найдутся три ребра, из которых можно составить треугольник. 6. К двум окружностям w1 и w2, пересекающимся в точках А и В, проведена их общая касательная CD (C и D — точки касания соответственно, точка B ближе к прямой CD, чем А). Прямая, проходящая через А, вторично пересекает w1 и w2 в точках К и L соответственно (A лежит между K и L). Прямые KC и LD пересекаются в точке p. Докажите, что РВ — симедиана треугольника KpL (прямая, симметричная медиане относительно биссектрисы). Олимпиадные задания по математике для учащихся 1-11 классов с решением и ответами: Свойства медианы треугольника. Итоговое повторение курса геометрии 7 – 9 классаСвойства медианы треугольника Итоговое повторение курса геометрии 7 – 9 класса При изучении какой-либо темы школьного курса можно отобрать определенный минимум задач, овладев методами решения которых, учащиеся будут в состоянии решить любую задачу на уровне программных требований по изучаемой теме. Предлагаю рассмотреть задачи, которые позволят увидеть взаимосвязи отдельных тем школьного курса математики. Поэтому составленная система задач является эффективным средством повторения, обобщения и систематизации учебного материала в ходе подготовки учащихся к экзамену. Для сдачи экзамена не лишними будут дополнительные сведения о некоторых элементах треугольника. Рассмотрим свойства медианы треугольника и задачи, при решении которых этими свойствами можно воспользоваться. В предложенных задачах реализуется принцип уровневой дифференциации. Все задачи условно поделены на уровни (уровень указан в скобках после каждого задания). Вспомним некоторые свойства медианы треугольника Свойство 1. Докажите, что медиана треугольника ABC, проведённая из вершины A, меньше полусуммы сторон AB и AC.
то, сложив почленно эти три неравенства, получим, что 2 Отсюда следует, что AM + BN + CK >
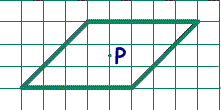
BA1 = AC, 2AM = AA1 SDEF’ , то SAED+SBFD>SDEF , следовательно, указанным образом расположить точки невозможно. так расположить точки нельзя. Источник: Окружная олимпиада (Москва) , 2008 г, 11 класс №32 Темы: Удвоение медианы. Ортоцентр и ортотреугольник Сложность:5 + Три точки, лежащие на одной прямой Подобные треугольники Классы: 9,10 В неравнобедренном треугольнике ABC точки H и M – точки пересечения высот и медиан соответственно. Через вершины A , B и C проведены прямые, перпендикулярные прямым AM , BM , CM соответственно. Докажите, что точка пересечения медиан треугольника, образованного проведенными прямыми, лежит на прямой MH .
Пусть A’B’C’ – треугольник, образованный проведенными прямыми и G – точка пересечения его медиан. Мы докажем, что M является серединой отрезка GH . Достроим треугольник BMC до параллелограмма BMCA1 . Отрезок MA1 делит сторону BC пополам, поэтому A1 лежит на прямой AM , причем AM = A1M (поскольку точка M делит медиану в отношении 2:1 ). Кроме того, BA1|| MC A’A1 сторонам треугольника A’B’C’ соответственно, поэтому эти треугольники подобны, причем соответствующие прямые BC и AG , содержащие медианы этих треугольников, перпендикулярны. Значит, прямая A’G совпадает с прямой A’A1 . Пусть G’ – точка, симметричная точке H относительно M . Треугольники AHM и A1G’M симметричны относительно M , поэтому A1G’|| AH Источник: Всероссийская олимпиада по математике, 2008 г, 9 класс Отрабатываем умение: самостоятельно решать задачи. Свойства медианы. Площадь треугольника 1. В треугольнике АВС медиана АМ перпендикулярна медиане BN. Найдите площадь треугольника АВС, если длина АМ равна 3, а длина BN равна 4. 2. Основание равнобедренного треугольника равно 2. Медианы, проведенные к боковым сторонам, взаимно перпендикулярны. Найдите площадь треугольника. 3. Две медианы равнобедренного треугольника взаимно перпендикулярны. Боковая сторона равна 4. В треугольнике АВС медианы АD и ВE перпендикулярны, 5. Сторона треугольника равна 20, а медианы, проведенные к двум другим сторонам – 24 и 18. Найдите площадь треугольника. 6. Стороны треугольника равны 13, 14 и 15. Найти площади треугольников, на которые разбивается данный треугольник его медианами. 7. Площадь треугольника АВС равна 12. Из вершины тупого угла В проведена медиана BD, длина которой равна 3. Найдите длину стороны АС, если угол ABD – прямой. 8. Найдите площадь треугольника, если две его стороны равны 1 и О т в е т: 1. Одна сторона треугольника равна а, другая – b. Найдите третью сторону, если известно, что она равна медиане, проведенной к ней. О т в е т: 2. Основание равнобедренного треугольника 3. В равнобедренном треугольнике основание равно 4. Медианы треугольника равны 5, 5. Числа Медиана, проведенная к гипотенузе 1. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна 3 см и делит прямой угол в отношении 2:1. Найдите меньший катет. 2. АА1, ВВ1, СС1 – медианы треугольника АВС. 3. Медианы треугольника АВС АА1, ВВ1 и СС1 пересекаются в точке О. 4. Гипотенуза прямоугольного треугольника в 4 раза больше проведенной к ней высоты. Найдите острые углы треугольника. О т в е т: 150; 750. 5. В трапеции ABCD углы при основании AD равны 200 и 700, длина отрезка, соединяющего середины оснований, равна 3. Найдите длину отрезка, соединяющего середины диагоналей трапеции. · , , Ленинградские математические кружки · , Задачи по планиметрии, Издательство МЦНМО, 2001г · интернет сайт http://zadachi. ***** Задачи по геометрии · Всероссийская олимпиада по математике, 2008 год, · Турнир им. Ломоносова, 2001 год · Московская математическая регата, 2012/13 г, 8 класс |


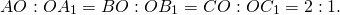

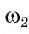 (0, R) с центром в точке О того же радиуса R и отмечаем ее точку пересечения F1 с лучом OF.
(0, R) с центром в точке О того же радиуса R и отмечаем ее точку пересечения F1 с лучом OF. (F1, A1C1).
(F1, A1C1). D1OF =
D1OF =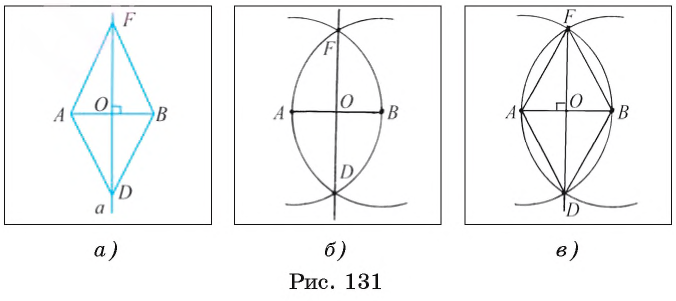
 AВ. Пусть, например, R = AB:
AВ. Пусть, например, R = AB:  BE, а точка Т лежит на луче, противоположном лучу ОВ. Из равенства прямоугольных треугольников FOT и DOT (FO = OD, катет ОТ — общий) следует, что FT = DT, т. е. точка Т принадлежит окружностям равных радиусов с центрами в точках F и D. Построив точку Т, мы построим биссектрису ВТ данного угла.
BE, а точка Т лежит на луче, противоположном лучу ОВ. Из равенства прямоугольных треугольников FOT и DOT (FO = OD, катет ОТ — общий) следует, что FT = DT, т. е. точка Т принадлежит окружностям равных радиусов с центрами в точках F и D. Построив точку Т, мы построим биссектрису ВТ данного угла.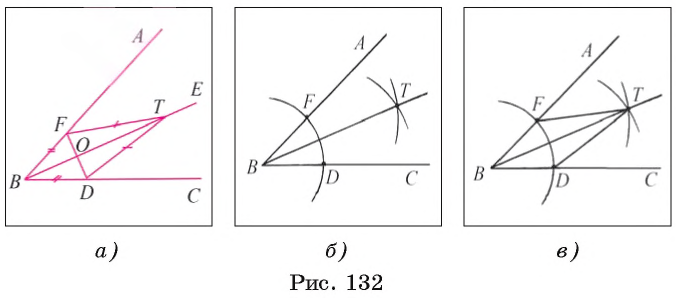








 Отложим на продолжении медианы AM за точку M отрезок MK, равный AM. Тогда в четырёхугольнике ABKC диагонали пересекаются и точкой пересечения делятся пополам. Значит, ABKC — параллелограмм. Применяя неравенство треугольника к треугольнику ABK, получим, что
Отложим на продолжении медианы AM за точку M отрезок MK, равный AM. Тогда в четырёхугольнике ABKC диагонали пересекаются и точкой пересечения делятся пополам. Значит, ABKC — параллелограмм. Применяя неравенство треугольника к треугольнику ABK, получим, что
 AM +
AM +  > AB + BC + AC.
> AB + BC + AC. (AB + BC + AC).
(AB + BC + AC). Отложим на продолжении медианы AM за точку M отрезок MA1, равный AM. Тогда ABA1C — параллелограмм. Поэтому
Отложим на продолжении медианы AM за точку M отрезок MA1, равный AM. Тогда ABA1C — параллелограмм. Поэтому Решение
Решение A’B’ и CA1|| MB
A’B’ и CA1|| MB  . Найдите площадь треугольника.
. Найдите площадь треугольника. ,
,  . Чему равен квадрат третьей стороны?
. Чему равен квадрат третьей стороны? , а медиана третьей стороны равна 2. (Указание – достроить до параллелограмма).
, а медиана третьей стороны равна 2. (Указание – достроить до параллелограмма). .
. .
. , медиана боковой стороны 5. Найдите длины боковых сторон.
, медиана боковой стороны 5. Найдите длины боковых сторон. , а угол при основании равен 300. Найдите длину медианы, проведенной к боковой стороне.
, а угол при основании равен 300. Найдите длину медианы, проведенной к боковой стороне. и
и  . Докажите, что треугольник прямоугольный.
. Докажите, что треугольник прямоугольный. ,
,  и
и  выражают длины медиан некоторого треугольника. Докажите, что если выполняется равенство
выражают длины медиан некоторого треугольника. Докажите, что если выполняется равенство  , то треугольник является прямоугольным.
, то треугольник является прямоугольным. . Найдите
. Найдите  .
. см.
см.  см. Найдите ВО.
см. Найдите ВО.