Вычислите координаты суммы данных векторов

Этот онлайн калькулятор позволит вам очень просто найти сумму двух векторов или разность двух векторов для плоских и пространственных задач.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на сложение и вычитание двух векторов и закрепить пройденый материал.

Видео:Координаты вектора. 9 класс.Скачать

Калькулятор для сложения и вычитания двух векторов

Введите значения векторов.

Инструкция использования калькулятора для сложения и вычитания двух векторов

Ввод даных в калькулятор для сложения и вычитания двух векторов

В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для сложения и вычитания двух векторов

• Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Теория. Сложение и вычитание двух векторов

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Сложение, вычитание, умножение на число векторов через координату. 9 класс.Скачать

Координаты вектора. Направляющие косинусы

Для решения задач с векторами необходимо определить вектор на плоскости или в пространстве, то есть дать информацию о его направлении и длине.

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Координаты вектора

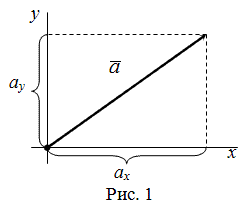
Пусть задана прямоугольная декартова система координат (ПДСК) $x O y$ и произвольный вектор $overline$, начало которого совпадает с началом системы координат (рис. 1).

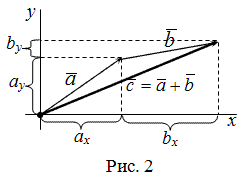
Сумма двух векторов, заданных координатами

Чтобы найти сумму двух векторов, заданных своими координатами, надо сложить их соответствующие координаты.

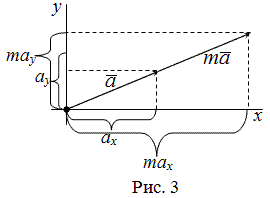
Умножение вектора на число

Чтобы умножить вектор на число, надо каждую координату этого вектора умножить на заданное число.

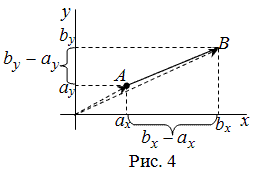
Рассмотрим далее случай, когда начало вектора не совпадает с началом системы координат. Предположим, что в ПДСК заданы две точки $Aleft(a_ ; a_right)$ и $Bleft(b_ ; b_right)$. Тогда координаты вектора $overline=left(x_ ; y_right)$ находятся по формулам (рис. 4):

Чтобы найти координаты вектора, заданного координатами начала и конца, надо от координат конца отнять соответствующие координаты начала.

Задание. Найти координаты вектора $overline$, если $A(-4 ; 2), B(1 ;-3)$

Решение. $overline=(1-(-4) ;-3-2)=(5 ;-5)$

Видео:9 класс, 2 урок, Координаты вектораСкачать

Направляющие косинусы

Направляющими косинусами вектора называются косинусы углов, образованных вектором с положительными направлениями осей координат.

Направление вектора однозначно задается направляющими косинусами. Для единичного вектора направляющие косинусы равны его координатам.

Здесь $alpha$, $beta$ и $gamma$ — углы, которые составляет вектор с положительными направлениями осей $O x$, $O y$ и $O z$ соответственно.

Основное свойство направляющих косинусов

Сумма квадратов направляющих косинусов равна единице.

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Основные сведения о сумме двух векторов

Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Основные понятия

Направленный отрезок, то есть отрезок, который имеет длину и определенное направление, носит название вектора.

Обозначается буквенным символом со стрелкой над ним:

Сонаправленные векторы — это векторы, направления которых совпадают (одинаковые по направлению).

Противоположно направленные векторы — это векторы, которые направлены в разные стороны.

С векторами можно производить такие операции, как:

Для начала, рассмотрим подробно сложение.

Сложение (сумма) векторов «a + b» — это операция вычисления вектора c, все элементы которого равны попарной сумме соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен:

Вычитание (разность) векторов «a — b» — это операция вычисления вектора c, все элементы которого равны попарной разности соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен:

Сложение векторов может осуществляться по трем правилам:

1. Правило параллелограмма. Из произвольной точки необходимо отложить два данных вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, будет суммой заданных векторов.
2. Правило многоугольника. Из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее. Когда все векторы отложены, соединим начальную точку с концом последнего вектора и получим сумму нескольких векторов.
3. Правило треугольника.

Видео:Вычитание векторов. 9 класс.Скачать

Сумма сонаправленных и противоположно направленных векторов, правило треугольника

Правило треугольника заключается в следующем: для того чтобы сложить два сонаправленных вектора, необходимо из произвольной точки отложить первый вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало первого с концом второго. Конечный вектор и будет суммой двух векторов.

Чертеж поможет наглядно объяснить правило:

AC — сумма векторов.

Разность векторов a и b является суммой векторов a и -b.

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Как вычислить координаты суммы двух векторов, пояснение на примерах

Кроме геометрического способа сложения (вычитания) векторов (правила треугольника, параллелограмма, многоугольника), существует способ сложения координат векторов.

Для того чтобы найти координаты суммы двух векторов, нужно сложить их соответствующие координаты по следующей формуле:

Найти сумму векторов a(7;5) и b(3;8)

Найти сумму координат векторов a(-7;2), b(-3;6), c(6;-5)

Видео:Геометрия, 9 класс, Правила нахождения координат суммы, разности векторов, произведенияСкачать

Примеры решения задач

Найти сумму векторов a(1;2), b(7;9)

Найти разность координат векторов a(4;-6), b(5;-1)

🎦 Видео

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Векторы. Метод координат. Вебинар | МатематикаСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Коллинеарность векторовСкачать

СУММА ВЕКТОРОВ правило треугольникаСкачать

Сложение и вычитание векторов через координаты. Практическая часть. 11 класс.Скачать

Скалярное произведение векторов. 9 класс.Скачать

Координаты точки и координаты вектора 1.Скачать

Как выразить вектор через данные векторы параллелограмма. Векторы на плоскости. Геометрия 8-9 классСкачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать