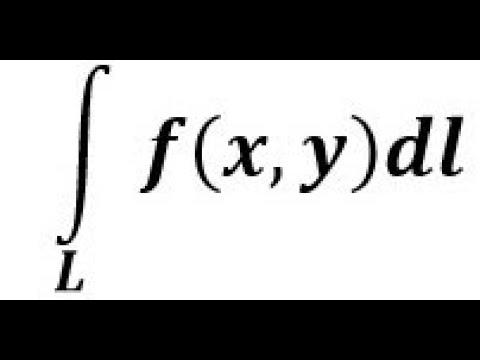Вычислить криволинейный интеграл 1 рода где l дуга окружности

Видео:Математический анализ, 47 урок, Криволинейные интегралы первого родаСкачать

Понятие криволинейного интеграла

Криволинейные интегралы — обобщение понятия определённого интеграла на случай, когда областью интегрирования является отрезок некоторой кривой, лежащий в плоскости. Общая запись криволинейного интеграла следующая:

где f(x, y) — функция двух переменных, а L — кривая, по отрезку AB которой происходит интегрирование. Если подынтегральная функция равна единице, то криволинейный интеграл равен длине дуги AB.

Как всегда в интегральном исчислении, криволинейный интеграл понимается как предел интегральных сумм каких-то очень маленьких частей чего-то очень большого. Что же суммируется в случае криволинейных интегралов?

Пусть на плоскости расположен отрезок AB некоторой кривой L, а функция двух переменных f(x, y) определена в точках кривой L. Пусть мы выполняем с этим отрезком кривой следующий алгоритм.

1. Разделить кривую AB на части точками (рисунки ниже).
2. В каждой части свободно выбрать точку M.
3. Найти значение функции в выбранных точках.
4. Значения функции умножить на
   • длины частей в случае криволинейного интеграла первого рода;
   • проекции частей на ось координат в случае криволинейного интеграла второго рода.
5. Найти сумму всех произведений.
6. Найти предел найденной интегральной суммы при условии, что длина самой длинной части кривой стремится к нулю.

Если упомянутый предел существует, то этот предел интегральной суммы и называется криволинейным интегралом от функции f(x, y) по кривой AB.

Случай криволинейного интеграла
первого рода

Случай криволинейного интеграла
второго рода

Введём следующие ообозначения.

M i (ζ i ; η i ) — выбранная на каждом участке точка с координатами.

f i (ζ i ; η i ) — значение функции f(x, y) в выбранной точке.

Δs i — длина части отрезка кривой (в случае криволинейного интеграла первого рода).

Δx i — проекция части отрезка кривой на ось Ox (в случае криволинейного интеграла второго рода).

d = maxΔs i — длина самой длинной части отрезка кривой.

Криволинейные интегралы первого рода

Исходя из вышеизложенного о пределе интегральных сумм, криволинейный интеграл первого рода записывается так:

.

Криволинейный интеграл первого рода обладает всеми свойствами, которыми обладает определённый интеграл. Однако есть одно важное различие. У определённого интеграла при перемене местами пределов интегрирования знак меняется на противоположный:

.

В случае же криволинейного интеграла первого рода не имеет значения, какую из точек кривой AB (A или B) считать началом отрезка, а какую концом, то есть

.

Криволинейные интегралы второго рода

Исходя из изложенного о пределе интегральных сумм, криволинейный интеграл второго рода записывается так:

.

В случае криволинейного интеграла второго рода при перемене местами начала и конца отрезка кривой знак интеграла меняется:

.

При составлении интегральной суммы криволинейного интеграла второго рода значения функции f i (ζ i ; η i ) можно умножать также на проекции частей отрезка кривой на ось Oy. Тогда получим интеграл

.

На практике обычно используется объединение криволинейных интегралов второго рода, то есть две функции f = P(x, y) и f = Q(x, y) и интегралы

,

а сумма этих интегралов

называется общим криволинейным интегралом второго рода.

Видео:Криволинейный интеграл 1 родаСкачать

Вычисление криволинейных интегралов первого рода

Вычисление криволинейных интегралов первого рода сводится к вычислению определённых интегралов. Рассмотрим два случая.

Кривая дана в декартовых прямоугольных координатах

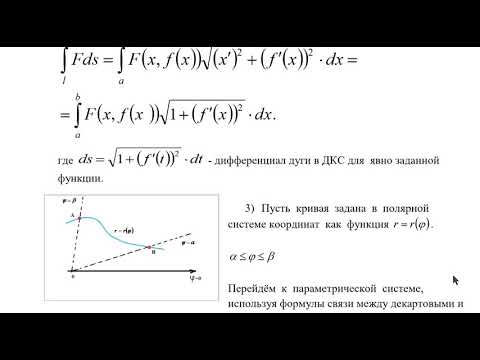
Пусть на плоскости задана кривая y = y(x) и отрезку кривой AB соответствует изменение переменной x от a до b. Тогда в точках кривой подынтегральная функция f(x, y) = f(x, y(x)) («игрек» должен быть выражен через «икс»), а дифференциал дуги и криволинейный интеграл можно вычислить по формуле

.

Если интеграл проще интегрировать по y, то из уравнения кривой нужно выразить x = x(y) («икс» через «игрек»), где и интеграл вычисляем по формуле

.

Пример 1. Вычислить криволинейный интеграл

,

где AB — отрезок прямой между точками A(1; −1) и B(2; 1) .

Решение. Составим уравнение прямой AB , используя формулу (уравнение прямой, проходящей через две данные точки A(x 1 ; y 1 ) и B(x 2 ; y 2 ) ):

.

Из уравнения прямой выразим y через x :

.

Тогда и теперь можем вычислять интеграл, так как у нас остались одни «иксы»:

Кривая дана в параметрической форме

Пусть в пространстве задана кривая

Тогда в точках кривой функцию нужно выразить через параметр t () а дифференциал дуги , поэтому криволинейный интеграл можно вычислить по формуле

Аналогично, если на плоскости задана кривая

,

то криволинейный интеграл вычисляется по формуле

.

Пример 2. Вычислить криволинейный интеграл

,

где L — часть линии окружности

,

находящаяся в первом октанте.

Решение. Данная кривая — четверть линии окружности, расположенная в плоскости z = 3 . Она соответствует значениям параметра . Так как

,

то дифференциал дуги

Подынтегральную функцию выразим через параметр t :

.

Теперь, когда у нас всё выражено через параметр t , можем свести вычисление данного криволинейного интеграла к определённому интегралу:

Видео:Криволинейный интеграл по длине дуги ➜ Криволинейный интеграл 1-го родаСкачать

Вычисление криволинейных интегралов второго рода

Так же, как и в случае криволинейных интегралов первого рода, вычисление интегралов второго рода сводится к вычислению определённых интегралов.

Кривая дана в декартовых прямоугольных координатах

Пусть дана кривая на плоскости уравнением функции «игрек», выраженной через «икс»: y = y(x) и дуге кривой AB соответствует изменение x от a до b . Тогда в подынтегральную функцию подставим выражение «игрека» через «икс» и определим дифференциал этого выражения «игрека» по «иксу»: . Теперь, когда всё выражено через «икс», криволинейный интеграл второго рода вычисляется как определённый интеграл:

Аналогично вычисляется криволинейный интеграл второго рода, когда кривая дана уравнением функции «икс», выраженной через «игрек»: x = x(y) , . В этом случае формула для вычисления интеграла следующая:

Пример 3. Вычислить криволинейный интеграл

, если

а) Вычислим криволинейный интеграл по отрезку прямой (на рисунке — синяя). Напишем уравнение прямой и выразим «игрек» через «икс»:

.

Получаем dy = dx . Решаем данный криволинейный интеграл:

б) если L — дуга параболы y = x² , получим dy = 2xdx . Вычисляем интеграл:

В только что решённом примере получили в двух случаях один и тот же результат. И это не совпадение, а результат закономерности, так как данный интеграл удовлетворяет условиям следующей теоремы.

Теорема. Если функции P(x,y) , Q(x,y) и их частные производные , — непрерывные в области D функции и в точках этой области частные производные равны, то криволинейный интеграл не зависит от пути интегрирования по линии L , находящейся в области D .

Кривая дана в параметрической форме

Пусть в пространстве дана кривая

.

,

а в подынтегральные функции подставим

—

выражения этих функций через параметр t . Получаем формулу для вычисления криволинейного интеграла:

Пример 4. Вычислить криволинейный интеграл

,

отвечающая условию y ≥ 0 .

Решение. Данная кривая — часть эллипса, находящаяся в плоскости z = 2 . Она соответствует значению параметра .

,

можем представить криволинейный интеграл в виде определённого интеграла и вычислить его:

Если дан криволинейный интеграл и L — замкнутая линия, то такой интеграл называется интегралом по замкнутому контуру и его проще вычислить по формуле Грина.

Видео:Математический анализ, 48 урок, Криволинейные интегралы второго родаСкачать

Больше примеров вычисления криволинейных интегралов

Пример 5. Вычислить криволинейный интеграл

,

где L — отрезок прямой между точками её пересечения с осями координат.

Решение. Определим точки пересечения прямой с осями координат. Подставив в уравнение прямой y = 0 , получим , . Подставив x = 0 , получим , . Таким образом, точка пересечения с осью Ox — A(2; 0) , с осью Oy — B(0; −3) .

Из уравнения прямой выразим y :

.

, .

Теперь можем представить криволинейный интеграл в виде определённого интеграла и начать вычислять его:

В подынтегральном выражении выделяем множитель , выносим его за знак интеграла. В получившемся после этого подынтегральном выражении применяем подведение под знак дифференциала и окончательно получаем:

Пример 6. Вычислить криволинейный интеграл

,

где L — дуга параболы между точками О(0; 0) и B(2; 2) .

Решение. Так как , то .

Теперь можем представить криволинейный интеграл в виде определённого интеграла и вычислить его:

Пример 7. Вычислить криволинейный интеграл

,

где L — дуга астроиды

в первом квадранте.

Решение. В первом квадранте . Определим дифференциал дуги:

Представляем криволинейный интеграл в виде определённого интеграла и вычисляем его:

Пример 8. Вычислить криволинейный интеграл

,

где L — первая арка циклоиды

Решение. Циклоида образует первую арку при изменении параметра t от 0 до 2π . Определим дифференциал дуги:

.

Подставим в криволинейный интеграл dl и y , выраженные через параметр t и получаем:

Пример 9. Вычислить криволинейный интеграл

,

где L — отрезок прямой от точки A(1; 1) до точки B(3; 5) .

Решение. Составим уравнение прямой AB :

.

Из полученного уравнения прямой выразим «игрек»:

Поэтому и теперь можем вычислить данный криволинейный интеграл:

Пример 10. Вычислить криволинейный интеграл

,

где L — первая арка циклоиды

Решение. Из уравнений кривой следует

.

Так как циклоида образует первую арку при изменении параметра t от 0 до 2π , то получаем соответствующие пределы интегрирования. Решаем данный криволинейный интеграл:

.

Уравнением кривой M 0 M 1 является y = 1 , тогда dy = 0 , на кривой M 1 M x — константа, значит, dx = 0 . Продолжаем и завершаем решение:

Вычисление длины дуги кривой

Если подынтегральная функция равна единице, то криволинейный интеграл первого рода равен длине дуги кривой L:

.

Пример 12. Вычислить длину дуги кривой

,

где .

Решение. Составляем криволинейный интеграл первого рода:

.

Определим производную «игрека»:

.

Продолжаем и завершаем решение:

Вычисление площади участка плоскости

Если границей участка D плоскости является кривая L, то площадь участка D можно вычислить в виде криволинейного интеграла второго рода

.

Пример 13. Вычислить площадь участка плоскости, ограниченного эллипсом

.

Решение. Площадь участка плоскости можно вычислить как криволинейный интеграл второго рода

,

где L — замкнутая линия, ограничивающая участок. Так как

.

Вычисление площади цилиндрической поверхности

Пусть на плоскости xOy дана гладка кривая L, в точках которой определена непрерывная функция двух переменных . Построим цилиндрическую поверхность, образующая которой параллельна оси Oz, и которая заключена между кривой L и поверхностью . Площадь этой цилиндрической поверхности можно вычислить по формуле

.

Вычисление массы материальной кривой

Если L — материальная кривая с плотностью , то массу материальной кривой можно вычислить по формуле

Определение статических моментов материальной кривой

Статические моменты материальной кривой с плотностью относительно осям координат вычисляются по формулам

,

.

Вычисление моментов инерции материальной кривой

Моменты инерции материальной кривой с плотностью относительно осей координат и начала системы координат можно вычислить по формулам

,

,

.

Вычисление координат центра тяжести материальной кривой

Координаты центра тяжести материальной кривой с плотностью можно определить по формулам

,

.

Вычисление работы силы

Если под воздействием переменной силы материальная точка перемещается из точки M в точку N по кривой L=MN, то приложенную работу можно вычислить по формуле

.

Пример 14. В каждой точке плоскости действует сила . Вычислить работу, совершаемую силой при перемещении единицы массы по дуге параболы из точки O(0;0) в точку А(4;2) .

Решение. Работу силы вычислим как криволинейный интеграл второго рода

.

Используя уравнение параболы, производим замену переменной

Видео:Криволинейный интеграл первого родаСкачать

Вычислить криволинейный интеграл 1 рода где l дуга окружности

Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Видео:Криволинейный интеграл 1-го рода ★ Криволинейный интеграл по длине дуги ★ ∫(x+y)dsСкачать

Примеры решений криволинейных интегралов

В этом разделе вы найдете подробные решения криволинейных интегралов первого и второго рода (непосредственное вычисление, по разным путям, по формуле Грина), а также применение к вычислению моментов инерции, массы, работы, силы притяжения и т.п.

Видео:Найдите массу дуги окружности ➜ Физический смысл криволинейного интеграла 1-го рода (по длине дуги)Скачать

Криволинейные интегралы 1-го рода: примеры решений

Задача 1. Вычислить криволинейный интеграл первого рода по указанной кривой $L$:

Задача 2. Вычислить криволинейный интеграл I рода $int_L y^2 dl$, $L$ — арка циклоиды $x=(t-sin t)/2$, $y=(1-cos t)/2$, $0 le t le pi$.

Задача 3. Вычислить криволинейный интеграл $int_L y^2 dl$, где $L$ – дуга параболы $y^2=2x$ от точки $(0;0)$ до точки $(1;sqrt)$.

Если вам нужна помощь в нахождении интегралов, выполнении домашней работы, будем рады принять ваш заказ на решение. Стоимость от 100 рублей, срок от нескольких часов.

Видео:Криволинейный интеграл II рода вдоль плоской кривойСкачать

Криволинейные интегралы 2-го рода: примеры решений

Задача 4. Вычислить криволинейный интеграл второго рода, взятый вдоль ориентированной кривой $L$: $int_L x^2 dy -xydx$, где $L$ — часть кривой $x^4-y^4=6x^2y$ от точки $A=(-4sqrt;4)$ до точки $B=(0;0)$

Задача 5. Вычислить интеграл $$int_L z^2x dx +(z+x+y)dy +y^2zdz,$$ где $L$ — кривая $a^2+y^2=ax, x^+y^2=z^2$ положительно ориентированная на внешней стороне цилиндра.

Задача 6. Вычислить криволинейный интеграл $int_ (y^2+x)dx+2x/y dy$ вдоль кривой $y=e^x$ от точки $A(0;1)$ до точки $B(1;e)$.

Задача 7. Проверить, что криволинейный интеграл не зависит от пути интегрирования и найти его значение.

Задача 8. Проверить криволинейный интеграл, который не зависит от пути интегрирования, и найти его значение (двумя способами – непосредственно и с помощью потенциала).

Задача 9. Вычислить криволинейный интеграл по замкнутому контуру в положительном направлении, используя формулу Грина

$$int_l (x-y^2)dy + (x^3+3y)dx, quad l: x=y, y=x^2.$$

Трудности с задачами? МатБюро поможет с интегралами.

Видео:Криволинейные интегралы 1-ого родаСкачать

Моменты инерции: примеры решений

Задача 10. Найти моменты инерции относительно осей однородных дуг $L$ плотности $rho$.

Задача 11. Вычислить момент инерции верхней половины окружности $x^2+y^2=a^2$ относительно оси $Oy$, если плотность $delta=1$.

Видео:Формула ГринаСкачать

Другие задания: примеры решений

Задача 12. Найти координаты силы притяжения дугой астроиды $x=a cos^3 t$, $y=a sin^3 t$, $0 le t le pi/2$ единичной массы, помещенной в начале координат, если плотность астроиды в каждой ее точке равна кубу расстояния этой точки от начала координат.

Задача 13. Вычислить работу силы $F(z,-x,y)$ вдоль дуги винтовой линии $z=2cos t$, $y=3sin t$, $z=4t$, $0 le t le 2pi$.

Задача 14. Доказать, что данное выражение $P(x,y)dx+Q(x,y)dy$ является полным дифференциалом функции $Ф(x,y)$ и найти ее с помощью криволинейного интеграла.

Задача 15. Вычислить работу силы $overline$ при перемещении точки приложения силы вдоль заданной кривой $L$ от точки $B$ до точки $C$, если значения параметра $t$ в точках $B$ и $C$ заданы.

$$ overline=-x overline+2y^2overline, quad x=2cos t, y=sint, quad t_B=0, t_C=pi/6. $$

Задача 16. Вычислить массу кривой $y=x^2/2$, где $xin (sqrt, 2sqrt)$, если линейная плотность задана функцией $f(x,y)=6y/x$.

📽️ Видео

Криволинейный интеграл 1 рода (по длине) | Решение задач 3.1 | ИнтФНПСкачать

Криволинейный интеграл 1 рода.Скачать

Криволинейный интеграл первого рода. ТемаСкачать

Криволинейный интеграл 1-го родаСкачать

Примеры вычисления криволинейного интеграла 1-го рода. Часть 1Скачать

Криволинейные интегралы по длине дуги. Примеры.Скачать

Криволинейные интегралы 1 и 2 рода – что такое и в чём разница? | Лекция 27 | МатанализСкачать

Криволинейный интеграл 1 рода.Скачать

Криволинейные интегралы первого и второго родаСкачать