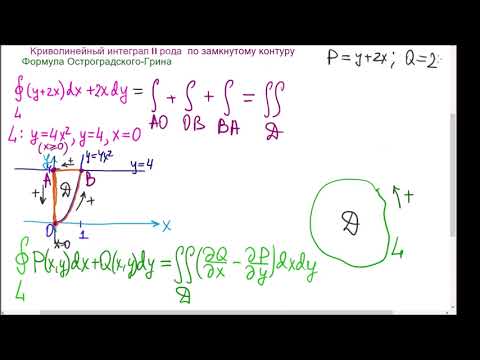
Если дан криволинейный интеграл, а кривая, по которой происходит интегрирование — замкнутая (называется контуром), то такой интеграл называется интегралом по замкнутому контуру и обозначается следующим образом:
.
Область, ограниченную контуром L обозначим D. Если функции P(x, y) , Q(x, y) и их частные производные 
и 
— функции, непрерывные в области D, то для вычисления криволинейного интеграла можно воспользоваться формулой Грина:
.
Таким образом, вычисление криволинейного интеграла по замкнутому контуру сводится к вычислению двойного интеграла по области D.
Формула Грина остаётся справедливой для всякой замкнутой области, которую можно проведением дополнительных линий на конечное число простых замкнутых областей.
Пример 1. Вычислить криволинейный интеграл
,
если L — контур треугольника OAB , где О(0; 0) , A(1; 2) и B(1; 0) . Направление обхода контура — против часовой стрелки. Задачу решить двумя способами: а) вычислить криволинейные интегралы по каждой стороне треугольника и сложить результаты; б) по формуле Грина.
а) Вычислим криволинейные интегралы по каждой стороне треугольника. Сторона OB находится на оси Ox , поэтому её уравнением будет y = 0 . Поэтому dy = 0 и можем вычислить криволинейный интеграл по стороне OB :
Уравнением стороны BA будет x = 1 . Поэтому dx = 0 . Вычисляем криволинейный интеграл по стороне BA :
Уравнение стороны AO составим, пользуясь формулой уравнения прямой, проходящей через две точки:
.
Таким образом, dy = 2dx . Вычисляем криволинейный интеграл по стороне AO :
Данный криволинейный интеграл будет равен сумме интегралов по краям треугольника:
.
б) Применим формулу Грина. Так как 
, 
, то 
. У нас есть всё для того, чтобы вычислить данный интеграл по замкнутому контуру по формуле Грина:
Как видим, получили один и тот же результат, но по формуле Грина вычисление интеграла по замкнутому контуру происходит значительно быстрее.
Пример 2. Пользуясь формулой Грина, вычислить криволинейный интеграл
,
где L — контур OAB , OB — дуга параболы y = x² , от точки О(0; 0) до точки A(1; 1) , AB и BO — отрезки прямых, B(0; 1) .
Решение. Так как функции 
, 
, а их частные производные 
, 
, D — область, ограниченная контуром L , у нас есть всё, чтобы воспользоваться формулой Грина и вычислить данный интеграл по замкнутому контуру:
Пример 3. Пользуясь формулой Грина, вычислить криволинейный интеграл
, если L — контур, который образуют линия y = 2 − |x| и ось Oy .
Решение. Линия y = 2 − |x| состоит из двух лучей: y = 2 − x , если x ≥ 0 и y = 2 + x , если x .
Имеем функции 
, 
и их частные производные 
и 
. Подставляем всё в формулу Грина и получаем результат:
Пример 4. С помощью формулы Грина вычислить криволинейный интеграл
,
если L — окружность 
.
Решение. Функции 
, 
и их частные производные 
и 
непрерывны в замкнутом круге . Подставляем всё в формулу Грина и вычисляем данный интеграл:
Видео:Математический анализ, 47 урок, Криволинейные интегралы первого родаСкачать
Вычислить интеграл по контуру треугольника
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
 |
|
Администратор, решение задач
Роман
Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym
Решение задач
Андрей
facebook:
dniprovets25
Видео:Криволинейный интеграл 1 родаСкачать
Формула Грина
Формула Грина
- Услуги проектирования
- Криволинейный интеграл
- Формула Грина
Видео:Математический анализ, 48 урок, Криволинейные интегралы второго родаСкачать
Формула Грина
Связность, односвязность, многосвязность
Напомним определения ряда понятий из теории функций нескольких переменных, которыми нам придется пользоваться.
Множество точек называется связным, если любые две точки этого множества можно соединить непрерывной кривой, целиком принадлежащей этому множеству.
Область называется односвязной, если любой замкнутый контур, лежащий в этой области, можно непрерывной деформацией стянуть в точку, не выходя при этом за пределы области.
Примеры:
Односвязны шар, параллелепипед и вообще любой выпуклый объём в пространстве. Односвязен шаровой слой, заключённый между двумя сферами. Пример неодносвязной области: тор. Все пространство односвязно и остаётся односвязным, если из него удалить точку или отрезок. Если же удалить из пространства прямую, оно потеряет свойство односвязности: окружность, охватывающую эту прямую, не удастся стянуть в точку, не пересекая прямую.
Кусочно-гладкая граница ограниченной односвязной области всегда связна, следовательно, является контуром.
Теорема Грина для односвязной области
Пусть на плоскости $mathbf > $ задана односвязная область$mathbf > $, ограниченная кусочно-гладким контуром $mathbf > $. На множестве $bar =Dcup C$ определены непрерывные функции $P(x,y)$ и $Q(x,y)$, имеющие непрерывные частные производные.
Доказательство
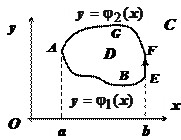
1). Пусть $mathbf > $ — простая область. Докажем сначала, что $ointlimits_C =-iintlimits_D dxdy > $.
$y=varphi _2 (x)y=varphi _1 (x)$
Опишем $mathbf >$ неравенствами $D:left( aleqslant xleqslant b, \ varphi _1 (x)leqslant yleqslant varphi _2 (x). \ end>right.$
Если контур включает вертикальные участки, такие как $mathbf > $, то на этих участках $mathbf > = 0$, поэтому $intlimits_ limits^cup > =0$, и $y=psi _2 (y)y=psi _1 (y)-iintlimits_D dxdy > =intlimits_ limits^cup > +intlimits_ limits^cup > +intlimits_ limits^cup > =ointlimits_C $, что и требовалось доказать.
Равенство $ointlimits_C =iintlimits_D dxdy > $ доказывается точно также:
Суммируя равенства $ointlimits_C =-iintlimits_D dxdy > $ и $ointlimits_C =iintlimits_D dxdy > $, получим одну из важнейших формул анализа — формулу Грина $ ointlimits_С -frac >right)dxdy > > $
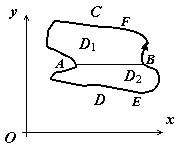
2). Пусть теперь $mathbf > $ — произвольная, не обязательно простая, область. Разобьём её на простые части. Пусть это разбиение производится отрезком $mathbf > $ и пусть подобласти $mathbf > _ $ и $mathbf > _ $ — результат разбиения. Для этих подобластей формула Грина доказана:
По свойству аддитивности $ointlimits_ =ointlimits_ +ointlimits_ $, $ointlimits_ =ointlimits_ +ointlimits_ = ointlimits_ -ointlimits_ $
Суммируя эти выражения, убеждаемся, что криволинейные интегралы по отрезкам $mathbf > $ и $mathbf > $ взаимно уничтожаются, а сумма интегралов по кривым $mathbf > $ и $mathbf > $ даёт интеграл по контуру $mathbf > $, т.е. формула Грина верна и для области, не являющейся простой.
Доказательство остаётся справедливым и в случае, когда разбиение производится добавлением большего числа, чем одна, кривых.
Теорема Грина для многосвязной области
Пусть теперь $mathbf > $ многосвязная на плоскости $mathbf > $. Граница многосвязной области состоит из нескольких связных частей, не имеющих общих точек.
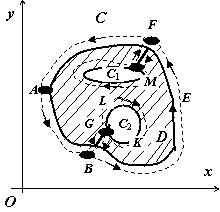
Рассмотрим случай, когда граница области $mathbf > $ состоит из внешнего контура $mathbf > $ и внутренних контуров $mathbf > _ $ и $mathbf > _ $.
Соединим контур $mathbf > $разрезом $mathbf > $ с контуром $mathbf > _ $, разрезом $mathbf > $ — с контуром $mathbf > _ $. > $ » подразумевается то, что мы удалим из $mathbf > $ отрезок $mathbf > )$.
Область $ ‘=Dbackslash (BGcup FM)$ с границей $ ‘=mathop limits^cup cup BGcup (C_2 =mathop limits^cup )cup GBcup mathop limits^cup cup FMcup C_1 cup MFcup mathop limits^cup $ односвязна, поэтому для неё справедлива формула Грина:
Двойные интегралы по областям $mathbf > $ и $ ‘mathbf $ равны ; в криволинейный интеграл по кусочно-гладкой кривой $ ‘$ интегралы по разрезам входят с противоположными знаками +Qdy$ и $intlimits_ +Qdy$, например > и поэтому взаимно уничтожаются, поэтому оказывается справедлива теорема Грина для многосвязной области :
пусть на плоскости $mathbf > $ дана многосвязная область$mathbf > $ с границей $Gamma $. На множестве $bar =Dcup Gamma $ определены непрерывные функции $P(x,y)$ и $Q(x,y)$, имеющие непрерывные частные производные. Тогда $ointlimits_Gamma -frac >right)dxdy > > $, при этом каждая часть полной границы $Gamma $ обходится так, что область $mathbf > $ остаётся слева.
Далее:
Замыкание. Свойства замыкания. Теорема о сведении к заведомо полной системе
СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице
Векторное поле
Вычисление криволинейного интеграла первого рода. Примеры
Дифференциальные характеристики векторного поля
Вычисление криволинейного интеграла второго рода. Примеры.
Поток векторного поля через поверхность
Примеры применения цилиндрических и сферических координат
Логические операции над высказываниями
Критерий полноты . Лемма о несамодвойственной функции
Механические приложения тройного интеграла
Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам
Линейный интеграл и циркуляция векторного поля
Механические приложения криволинейного интеграла 1-го рода
📽️ Видео
Криволинейный интеграл по длине дуги ➜ Криволинейный интеграл 1-го родаСкачать
Криволинейный интеграл II рода вдоль плоской кривойСкачать
Интегрирование комплексной функцииСкачать
ТФКП. Вычислить интеграл по замкнутому контуру с помощью вычетов. Пример из ДемидовичаСкачать
Криволинейный и двойной интеграл. Формула Грина.Ч1Скачать
Применение определенного интеграла при решении геометр. и физических задач. Практ. часть. 11 класс.Скачать
Криволинейная трапеция и ее площадь. 11 класс.Скачать
Интеграл по замкнутому контуру.Без формулы ГринаСкачать
Вычислить интеграл по заданному контуру. Интегрирование по части окружности и по отрезку прямой.Скачать
ТФКП. Вычисление интегралов с помощью вычетов. Теорема Коши о вычетах. Примеры решенийСкачать
Циркуляция векторного поля. Вычисление при при помощи криволинейного интеграла.Скачать
ТФКП. Интегральная формула Коши. Примеры решений типовых задач. Решение контурных интегралов.Скачать
Формула ГринаСкачать
