Коэффициент трения качения сталь по стали по окружности

Каждый человек, который так или иначе связан с техникой, знает, что собой представляет сила трения. В нашей жизни она может играть как положительную, так и отрицательную роль. Данную статью посвятим вопросу определения коэффициента трения стали по стали.

Виды трения

До того как рассмотреть вопрос определения коэффициента трения стали по стали, следует ближе познакомиться с трением между твердыми телами. Рассмотрим подробнее:

• Если привести в соприкосновение два твердых тела, то для осуществления смещения их друг относительно друга потребуется приложить некоторую силу. Она должна быть больше трения покоя, которое движению препятствует.
• Как только тела начинают взаимное перемещение, их поверхности трутся друг о друга. Соответствующая сила, сопротивляющаяся движению, связана с трением скольжения.
• Третий вид — это трение качения. Исходя из названия видно, оно возникает, когда тела катятся друг по другу, например, колесо велосипеда по асфальту.

Все три вида трения действуют в области контакта твердых поверхностей. Соответствующие силы всегда стремятся замедлить любое движение.

Польза сил трения связана с тем, что они обеспечивают возможность самого движения и изменения его характеристик. Вред же, как правило, связан с энергетическими потерями во время перемещения и с износом трущихся материалов.

Трение покоя и скольжения: коэффициент трения стали по стали

Пришло время рассмотреть формулы. Для расчета сил трения скольжения и покоя используют следующее выражение в физике:

Здесь µ и N — коэффициент силы трения и реакция опоры, соответственно. Поясним это. Величина µ для рассматриваемых видов трения главным образом зависит от шероховатости контактирующих поверхностей. Чем больше микроскопических неровностей содержат поверхности, тем больше ее значение.

Оно также определяется трущимися материалами. В случае стальных поверхностей большой вклад в характеристику этого коэффициента вносят металлические связи между атомами железа. Это связано с плотным соприкосновением стальных листов. Этот факт объясняет, почему полировка металлической поверхности может не только не уменьшить, но даже увеличить величину µ.

Для большинства видов стали значение µ для трения скольжения лежит в пределах 0,12-0,15, а для трения покоя эти пределы составляют 0,15-0,16. Смазка поверхностей приводит к снижению показателя (до 0,1 и меньше).

Трение качения и его коэффициент

Формула для определения силы трения качения имеет такую же форму, как для рассмотренных ранее видов. Запишем ее еще раз:

Коэффициент качения C_R зависит от твердости и упругих характеристик катящегося тела, а также от радиуса колеса (шарика, ролика).

Коэффициент трения стали по стали C_R важно учитывать при движении поезда. Его металлические колеса катятся по рельсам из такого же материала. Табличные данные говорят, что C_R для колес поезда лежит в пределах 0,0002-0,001.

Отметим, что сталь — это достаточно твердый материал, поэтому величина упругой деформации во время качения для него невелика. Последнее обуславливает малые значения C_R. Приведенные табличные данные говорят о том, что сила трения качения стали по стали в 100 и более раз меньше, чем аналогичная сила при скольжении металлических пластин друг по другу.

Задача на определение коэффициента трения

Стальной брус массой 1 кг прикрепили к динамометру и начали равномерно тянуть по стальному горизонтальному листу. Необходимо определить коэффициент трения при таком скольжении, если динамометр при равномерном движении бруса показывал значение силы 1,2 ньютона.

Для определения величины µ воспользуемся выражением для силы F_t, имеем:

Поскольку эксперимент проводится на горизонтальной поверхности, то реакция опоры N будет равна весу бруска. В итоге получаем конечную формулу для µ:

Осталось подставить данные и вычислить значение коэффициента скольжения стали по стали: µ = 0,12.

Коэффициенты трения покоя и трения качения

• 

Сила трения качения описывается как: Fтр=kтр(Fn/r) , где kтр- коэффициент трения а Fn — прижимающая сила, а r — радиус колеса. Размерность коэффициента трения качения, естественно, [длина]. Ниже приводится таблица полезных диапазонов коэффициентов трения качения для различных пар материалов в см.

Коэффициенты трения скольжения для различных материалов

Трущиеся поверхности	k
Бронза по бронзе	0,2
Бронза по стали	0,18
Дерево сухое по дереву	0,25 — 0,5
Деревянные полозья по снегу и льду	0,035
то же, но полозья обиты стальной полосой	0,02
Дуб по дубу вдоль волокон	0,48
тоже поперек волокон одного тела и вдоль волокон другого	0,34
Канат пеньковый мокрый по дубу	0,33
Канат пеньковый сухой по дубу	0,53
Кожаный ремень влажный по металлу	0,36
Кожаный ремень влажный по дубу	0,27 — 0,38
Кожаный ремень сухой по металлу	0,56
Колесо со стальным бандажом по стальному рельсу	0,16
Лед по льду	0,028
Медь по чугуну	0,27
Металл влажный по дубу	0,24-0,26
Металл сухой по дубу	0,5-0,6
Подшипник скольжения при смазке	0,02-0,08
Резина (шины) по твердому грунту	0,4-0,6
Резина (шины) по чугуну	0,83
Смазанный жиром кожаный ремень по металлу	0,23
Сталь (или чугун) по феродо* и райбесту*	0,25-0,45
Сталь по железу	0,19
Сталь по льду (коньки)	0,02-0,03
Сталь по стали	0,18
Сталь по чугуну	0,16
Фторопласт по нержавеющей стали	0,064-0,080
Фторопласт-4 по фторопласту	0,052-0,086
Чугун по бронзе	0,21
Чугун по чугуну	0,16
Примечание. Звездочкой отмечены материалы, применяемые в тормозных и фрикционных устройствах.

Таблица коэффициентов трения покоя (коэффициентов сцепления) для различных пар материалов.

Материал

Ксц

Химически чистые металл по металлу

совсем без окисных пленок (тщательно очищенные)100несмазанные на воздухе1,0смазанные минеральным маслом0,2-0,4смазанные растительными и животными маслами0,1

Сплавы, по стали

медно-свинцовый несмазанный0,2медно-свинцовый смазанный минеральным маслом0,1Сплав Вуда, белый металл = white metall несмазанный0,7Сплав Вуда, белый металл смазанный минеральным маслом0,1Фосфористая бронза, латунь несмазанная0,35Фосфористая бронза, латунь смазанная минеральным маслом0,15-0,2Сталь обычная несмазанная0,4Сталь обычная смазанная минеральным маслом0,1-0,2Стальные поверхности высокой твердости несмазанные0,6

Стальные поверхности высокой твердости при смазке:

— растительные и животные масла0,08-0,1— минеральные масла0,12— дисульфид молибдена0,1— олеиновая кислота0,08— спирт, бензин0,4— глицерин0,2Тонкая пленка индия толщиной 10 -3 -10 -4 см на твердом основании0,08Тонкая пленка свинца на твердом основании0,15Тонкая пленка меди на твердом основании0,3

Неметаллические материалы

стекло по стеклу, очищенные1стекло по стеклу, смазанные жидкими углеводородами или жирными кислотами0,3-0,6стекло по стеклу, смазанные твердыми углеводородами0,1Алмаз по алмазу, очищенные и дегазированные0,4Алмаз по алмазу, очищенные, на воздухе0,1Алмаз по алмазу, смазанные0,05-0,1Сапфир по сапфиру , очищенные и дегазированные0,6Сапфир по сапфиру, очищенные, на воздухе0,2Сапфир по сапфиру, смазанные0,15-0,2Графит по графиту, очищенные и дегазированные0,5-0,8Графит по графиту, очищенные, на воздухе0,1Графит по графиту, смазанные, на воздухе0,1Графит по стали, очищенный и смазанный0,1Каменная соль очищенная по каменной соли0,8Нитрат соды по нитрату соды очищенные0,5Нитрат соды по нитрату соды смазанные0,12Лед по льду при ниже -50°С0,5Лед по льду в диапазоне 0/ -20°С0,05-0,1Карбид вольфрама по стали, очищенные0,4-0,6Карбид вольфрама по стали, смазанные0,1-0,2Перпекс или полиэтилен по перпексу или полиэтилену, очищенные0,8Перпекс или полиэтилен по стали, очищенные0,3-0,5Нейлон по нейлону0,5ПТФЕ по ПТФЕ (Ф-4, фторопласт-4)0,04-0,1ПТФЕ по стали0,04-0,1Шерстяное волокно по роговине (материал вроде рога быка) , очищенное, по ворсу0,4-0,6Шерстяное волокно по роговине (материал вроде рога быка) , очищенное, против ворса0,8-0,1Шерстяное волокно по роговине (материал вроде рога быка) , смазанное, по ворсу0,3-0,4Шерстяное волокно по роговине (материал вроде рога быка) ,смазаное, против ворса0,5-0,3Хлопковая нить по хлопковой нити в состоянии поставки0,3Хлопок по хлопку (вата) в состоянии поставки0,6Шелк по шелку в состоянии поставки0,2-0,3Дерево по дереву, очищенное сухое0,2-0,5Дерево по дереву, очищенное влажное0,2Дерево по кирпичу, очищенное сухое0,3-0,4Кожа по металлу очищенная сухая0,6Кожа по металлу очищенная влажная0,4Кожа по металлу очищенная смазанная0,2Тормозной материал по чугуну очищенный0,4Тормозной материал по чугуну влажный0,2Тормозной материал по чугуну смазанный0,1

Коэффициенты трения качения.

Сила трения качения описывается как:

F_тр=k_тр(F_n/r) , где k_тр— коэффициент трения а F_n — прижимающая сила, а r — радиус колеса.

Размерность коэффициента трения качения, естественно, [длина].

Ниже приводится таблица полезных диапазонов коэффициентов трения качения для различных пар материалов в см.

Коэффициенты трения качения.

Стальное колесо по стали	0,001-0,05
Дереянное колесо по дереву	0,05-0,08
Стальное колесо по дереву	0,15-0,25
Пневматичекая шина по асфальту	0,006-0,02
Деревянное колесо по стали	0,03-0,04
Шарикоподшипник (подшипник качения)	0,001-0,004
Роликоподшипник (тоже качения)	0,0025-0,01
Шарик твердой стали по стали	0,0005-0,001

Сила трения скольжения — силы, возникающие между соприкасающимися телами при их относительном движении. Если между телами отсутствует жидкая или газообразная прослойка (смазка), то такое трение называется сухим. В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя.

Опытным путём установлено, что сила трения зависит от силы давления тел друг на друга (силы реакции опоры), от материалов трущихся поверхностей, от скорости относительного движения и не зависит от площади соприкосновения. (Это можно объяснить тем, что никакое тело не является абсолютно ровным. Поэтому истинная площадь соприкосновения гораздо меньше наблюдаемой. Кроме того, увеличивая площадь, мы уменьшаем удельное давление тел друг на друга.) Величина, характеризующая трущиеся поверхности, называется коэффициентом трения, и обозначается чаще всего латинской буквой «k» или греческой буквой «μ». Она зависит от природы и качества обработки трущихся поверхностей. Кроме того, коэффициент трения зависит от скорости. Впрочем, чаще всего эта зависимость выражена слабо, и если большая точность измерений не требуется, то «k» можно считать постоянным.

В первом приближении величина силы трения скольжения может быть рассчитана по формуле:

, где

— коэффициент трения скольжения,

— сила нормальной реакции опоры.

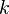
По физике взаимодействия трение принято разделять на:

• Сухое, когда взаимодействующие твёрдые тела не разделены никакими дополнительными слоями/смазками — очень редко встречающийся на практике случай. Характерная отличительная черта сухого трения — наличие значительной силы трения покоя.
• Сухое с сухой смазкой (графитовым порошком)
• Жидкостное, при взаимодействии тел, разделённых слоем жидкости или газа (смазки) различной толщины — как правило, встречается при трении качения, когда твёрдые тела погружены в жидкость;
• Смешанное, когда область контакта содержит участки сухого и жидкостного трения;
• Граничное, когда в области контакта могут содержатся слои и участки различной природы (окисные плёнки, жидкость и т. д.) — наиболее распространённый случай при трении скольжения.

В связи со сложностью физико-химических процессов, протекающих в зоне фрикционного взаимодействия, процессы трения принципиально не поддаются описанию с помощью методов классической механики.

При механических процессах всегда происходит в большей или меньшей степени преобразование механического движения в другие формы движения материи (чаще всего в тепловую форму движения). В последнем случае взаимодействия между телами носят названия сил трения.

Опыты с движением различных соприкасающихся тел (твёрдых по твёрдым, твёрдых в жидкости или газе, жидких в газе и т. п.) с различным состоянием поверхностей соприкосновения показывают, что силы трения проявляются при относительном перемещении соприкасающихся тел и направлены против вектора относительной скорости тангенциально к поверхности соприкосновения. При этом всегда происходит нагревание взаимодействующих тел.

Силами трения называются тангенциальные взаимодействия между соприкасающимися телами, возникающие при их относительном перемещении. Силы трения возникающие при относительном перемещении различных тел, называются силами внешнего трения.

Силы трения возникают и при относительном перемещении частей одного и того же тела. Трение между слоями одного и того же тела называется внутренним трением.

В реальных движениях всегда возникают силы трения большей или меньшей величины. Поэтому при составлении уравнений движения, строго говоря, мы должны в число действующих на тело сил всегда вводить силу трения F тр.

Тело движется равномерно и прямолинейно, когда внешняя сила уравновешивает возникающую при движении силу трения.

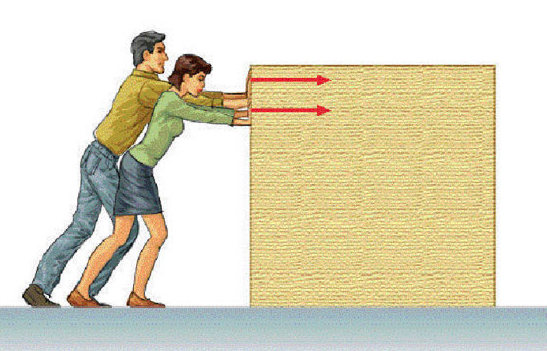
Для измерения силы трения, действующей на тело, достаточно измерить силу, которую необходимо приложить к телу, чтобы оно двигалось без ускорения.

Техническая механика

Трение — основные понятия, законы и зависимости

Трение качения

Трением качения называется трение движения, при котором скорости соприкасающихся тел в точках касания одинаковы по значению и направлению.

Если движение двух соприкасающихся тел происходит при одновременном качении и скольжении, то в этом случае возникает трение качения с проскальзыванием .

Рассмотрим качение без скольжения цилиндра весом G и радиусом r по горизонтальной опорной плоскости (см. рисунок 1) .
В результате действия силы G произойдет деформация цилиндра и опорной плоскости в месте их соприкосновения.
Если сила P не действует, то сила G будет уравновешиваться реакцией R опорной плоскости и цилиндр будет находиться в покое (реакция R будет вертикальна).
Если к цилиндру приложить небольшую силу Р , то он по-прежнему будет находиться в покое. При этом произойдет перераспределение давлений на опорную поверхность и полная реакция R пройдет через некоторую точку А и через точку О (согласно теореме о равновесии трех непараллельных сил).

При каком-то критическом значении силы Р цилиндр придет в движение и будет равномерно перекатываться по опорной плоскости, а точка А займет при этом крайнее правое положение.
Отсюда видно, что трение качения в состоянии покоя может изменяться от нуля до какого-то максимального значения, причем максимальным оно будет в момент начала движения.

Обозначим k максимальное значение плеча силы G относительно точки А . Тогда в случае равномерного перекатывания цилиндра (т. е. равновесия) :

ΣM_А = 0 или – Pr + Gh = 0 ,

причем плечо силы Р вследствие незначительности деформации тел считаем равным радиусу цилиндра r (сила Р – горизонтальная). Из последнего равенства определим силу, необходимую для равномерного качения цилиндра:

Максимальное значение плеча k называется коэффициентом трения качения; он имеет размерность длины и выражается в сантиметрах или миллиметрах.

Из полученной формулы видно, что усилие, необходимое для перекатывания цилиндрического катка, прямо пропорционально его весу G и обратно пропорционально радиусу r катка. Из этого следует, что каток, имеющий бóльший диаметр, легче перекатывать.

Коэффициент трения качения определяется опытным путем, его значения для различных условий приводятся в справочниках. Ниже приведены ориентировочные значения коэффициента трения качения k для катка по плоскости (см):

• Мягкая сталь по мягкой стали. 0,005
• Закаленная сталь по закаленной стали. 0,001
• Чугун по чугуну. 0,005
• Дерево по стали. 0,03. 0,04
• Дерево по дереву. 0,05. 0,08
• Резиновая шина по шоссе. 0,24

Коэффициент трения качения практически не зависит от скорости движения тела.

В ряде случаев при изучении трения качения активные и реактивные силы, действующие на каток, удобно представлять в ином виде (см. рисунок 2а, б) .

Разложим полную реакцию R опорной поверхности на составляющие N и F_тр , тогда:

где F_тр – сила трения качения; N — реакция, нормальная к недеформированной опорной плоскости.

Составим три уравнения равновесия катка:

ΣX = 0; P – F_тр = 0;
ΣY = 0; N – G = 0;
ΣM_А = 0; — Pr + Gk = 0.

Из этих уравнений имеем:

P = F_тр ; N = G ; Pr = Gk .

Введем обозначения Pr = M , Gk = M_тр , где М – момент трения качения, М_тр – момент трения.

Возможны следующие частные случаи качения цилиндрического катка:

• М ≥ М_тр, но Р F_тр – имеет место только скольжение;
• М > М_тр, но Р > F_тр – качение с проскальзыванием;
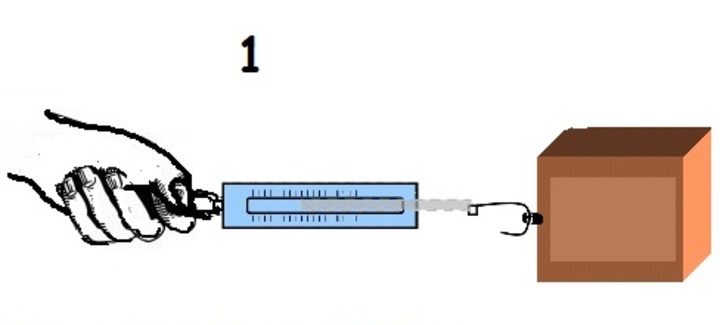
• М G , опирающееся на плоскость и способное опрокидываться вокруг какого-нибудь ребра под действием горизонтальной силы Р (см. рисунок 3) .
  Допустим, что силы Р и G лежат в одной плоскости, пересекающейся с ребром в точке А .
  В момент начала опрокидывания на тело будут действовать также нормальная реакция N_А и сила трения F_тр , приложенные в точке А , причем в случае равновесия системы всех четырех сил можно записать два уравнения равновесия:

ΣY = 0 ; N_А – G = 0 ; ΣX = 0 ; F_тр – P = 0 , откуда P = F_тр .

Таким образом, в момент начала опрокидывания через ребро А на рассматриваемое тело действует пара сил (Р,F_тр) , стремящихся опрокинуть тело, и пара сил (G,N_А) , противодействующих опрокидыванию.

Очевидно, что опрокидывание не произойдет, если М(G,N_А) > М(Р,F_тр) , или Gb > Pa .

Произведение Gb равно моменту силы G относительно точки А и называется моментом устойчивости .
Момент силы Р относительно той же точки, равный произведению Pa , называется опрокидывающим моментом .

Условие устойчивости против опрокидывания можно записать в виде неравенства:

Это выражение можно сформулировать следующим образом: для устойчивости твердого тела против опрокидывания необходимо и достаточно, чтобы момент устойчивости был больше опрокидывающего момента.

Если на тело действуют несколько сил, стремящихся его опрокинуть, то опрокидывающий момент равен сумме моментов этих сил относительно точки, вокруг которой может произойти опрокидывание. То же относится и к моменту устойчивости – если опрокидыванию тела препятствуют несколько сил, то момент устойчивости будет равен сумме моментов этих сил относительно точки (полюса) опрокидывания.

Отношение момента устойчивости к опрокидывающему моменту называется коэффициентом устойчивости:

Очевидно, что в сооружениях коэффициент устойчивости k_уст должен быть больше единицы.

Расчет на устойчивость особенно важен для высоких сооружений, таких, как дымовые трубы, высотные здания, мачты, краны и т. д. Подобные инженерные конструкции, как правило, подвержены горизонтальным опрокидывающим силам, вызываемым ветрами (ветровые нагрузки), что необходимо учитывать при расчетах подобных сооружений на устойчивость против опрокидывания.

Следует отметить, что в случае, когда Р > F_тр (опрокидывающая сила больше силы трения), а опрокидывающий момент меньше момента устойчивости М_опр , тело будет скользить по опорной плоскости, если, конечно, конструкция опоры тела допускает такое движение.

🔥 Видео