Если дан криволинейный интеграл, а кривая, по которой происходит интегрирование — замкнутая (называется контуром), то такой интеграл называется интегралом по замкнутому контуру и обозначается следующим образом:
.
Область, ограниченную контуром L обозначим D. Если функции P(x, y) , Q(x, y) и их частные производные 
и 
— функции, непрерывные в области D, то для вычисления криволинейного интеграла можно воспользоваться формулой Грина:
.
Таким образом, вычисление криволинейного интеграла по замкнутому контуру сводится к вычислению двойного интеграла по области D.
Формула Грина остаётся справедливой для всякой замкнутой области, которую можно проведением дополнительных линий на конечное число простых замкнутых областей.
Пример 1. Вычислить криволинейный интеграл
,
если L — контур треугольника OAB , где О(0; 0) , A(1; 2) и B(1; 0) . Направление обхода контура — против часовой стрелки. Задачу решить двумя способами: а) вычислить криволинейные интегралы по каждой стороне треугольника и сложить результаты; б) по формуле Грина.
а) Вычислим криволинейные интегралы по каждой стороне треугольника. Сторона OB находится на оси Ox , поэтому её уравнением будет y = 0 . Поэтому dy = 0 и можем вычислить криволинейный интеграл по стороне OB :
Уравнением стороны BA будет x = 1 . Поэтому dx = 0 . Вычисляем криволинейный интеграл по стороне BA :
Уравнение стороны AO составим, пользуясь формулой уравнения прямой, проходящей через две точки:
.
Таким образом, dy = 2dx . Вычисляем криволинейный интеграл по стороне AO :
Данный криволинейный интеграл будет равен сумме интегралов по краям треугольника:
.
б) Применим формулу Грина. Так как 
, 
, то 
. У нас есть всё для того, чтобы вычислить данный интеграл по замкнутому контуру по формуле Грина:
Как видим, получили один и тот же результат, но по формуле Грина вычисление интеграла по замкнутому контуру происходит значительно быстрее.
Пример 2. Пользуясь формулой Грина, вычислить криволинейный интеграл
,
где L — контур OAB , OB — дуга параболы y = x² , от точки О(0; 0) до точки A(1; 1) , AB и BO — отрезки прямых, B(0; 1) .
Решение. Так как функции 
, 
, а их частные производные 
, 
, D — область, ограниченная контуром L , у нас есть всё, чтобы воспользоваться формулой Грина и вычислить данный интеграл по замкнутому контуру:
Пример 3. Пользуясь формулой Грина, вычислить криволинейный интеграл
, если L — контур, который образуют линия y = 2 − |x| и ось Oy .
Решение. Линия y = 2 − |x| состоит из двух лучей: y = 2 − x , если x ≥ 0 и y = 2 + x , если x .
Имеем функции 
, 
и их частные производные 
и 
. Подставляем всё в формулу Грина и получаем результат:
Пример 4. С помощью формулы Грина вычислить криволинейный интеграл
,
если L — окружность 
.
Решение. Функции 
, 
и их частные производные 
и 
непрерывны в замкнутом круге . Подставляем всё в формулу Грина и вычисляем данный интеграл:
- Интеграл по замкнутому контуру окружности
- VMath
- Инструменты сайта
- Основное
- Навигация
- Информация
- Действия
- Содержание
- Глава 4. Интегрирование функций комплексного переменного
- Определение интеграла от функции комплексного переменного
- Интеграл по замкнутому контуру окружности
- Интеграл по замкнутому контуру, формула Грина, примеры
- Электронная библиотека
- 📹 Видео
Видео:Вычислить интеграл по заданному контуру. Интегрирование по части окружности и по отрезку прямой.Скачать
Интеграл по замкнутому контуру окружности
Видео:ТФКП. Интегральная формула Коши. Примеры решений типовых задач. Решение контурных интегралов.Скачать
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Видео:Математический анализ, 47 урок, Криволинейные интегралы первого родаСкачать
Глава 4. Интегрирование функций комплексного переменного
Видео:ТФКП. Вычислить интеграл по замкнутому контуру с помощью вычетов. Пример из ДемидовичаСкачать
Определение интеграла от функции комплексного переменного
Пусть $[a,b]$ — отрезок на вещественной оси. Образ при непрерывном отображении отрезка $[a,b]$ на комплексную плоскость называется непрерывной кривой: $$ Gamma= . $$ Непрерывная кривая называется кривой Жордана, если указанные отображения взаимно-однозначны, за исключением, может быть, одной точки на кривой, в которую могут отображаться концы отрезка $[a,b]$ (в таком случае кривая — замкнутая). Другими словами, кривая Жордана — непрерывная кривая без самопересечений.
Кривая Жордана называется гладкой, если в каждой ее точке существует касательная (отображение $z(t)$ — непрерывно дифференцируемо, то есть $x,yin C^1[a,b]$, причем $z'(t)neq0$).
Кривая Жордана называется спрямляемой, если она имеет длину. Гладкая кривая имеет длину, но существуют непрерывные кривые, не имеющие длины.
Пусть в области $D$ плоскости $z$ задана непрерывная функция $$ w=f(z)=u(x,y)+ mathbf i v(x,y) $$ и пусть $ell$ — кусочно-гладкая линия с началом в точке $z_0=a$ и концом в точке $z_n=b$, целиком лежащая в области $D$.
Задание начала и конца линии $ell$ ориентирует эту линию, т.е. устанавливает на ней положительное направление.
Линия $ell$ может быть как незамкнутой, так и замкнутой (в последнем случае $z_n=z_0$).
Любым образом разобьем линию $ell$ на $n$ элементарных дуг в направлении от $a$ к $b$ точками $z_1,dots,z_ $, где $z_k=x_k+iy_k$. Обозначим $$z_k-z_ =Delta z_k=Delta x_k+iDelta y_k,$$ где $$Delta x_k=x_k-x_ , ,,Delta y_k=y_k-y_ , ,, k=1,dots,n.$$ ($Delta z_k $ — вектор, идущий из точки $z_ $ в точку $z_k$, а $|Delta z_k|$ — длина этого вектора, т.е. длина хорды, стягивающей $k$-ую элементарную дугу).
В произвольном месте каждой элементарной дуги $(z_ ,z_k)$ возьмем соответственно по точке $t_k=xi_k+mathbf i eta_k$.
Составим сумму $$ sumlimits_ ^n f(t_k)Delta z_k=sumlimits_ ^n big(u(xi_k,eta_k)Delta x_k-v(xi_k,eta_k)Delta y_kbig)+ $$ $$ +mathbf i sumlimits_ ^nbig(v(xi_k,eta_k)Delta x_k+u(xi_k,eta_k) Delta y_kbig). $$
Через $max|Delta z_k|$ обозначим наибольшую из величин $|Delta z_k|$. В курсе математического анализа доказывается, что при условии $max|Delta z_k|to0$ (в этом случае $ntoinfty$) обе суммы в правой части формулы для непрерывных функций $u(x,y)$ и $v(x,y)$ $big($непрерывность этих функций следует из непрерывности $f(z)$$big)$ и кусочно-гладкой $ell$ стремятся к конечным пределам, не зависящими ни от способа разбиения $ell$ на элементарные дуги, ни от выбора точек $t_k$.
Эти пределы являются соответственно криволинейными интегралами второго рода $$ lim_ (mbox )= intlimits_ u(x,y),dx-v(x,y),dy+mathbf i intlimits_ v(x,y),dx+u(x,y),dy. $$
Следовательно, при $max|Delta z_k|to0$ и сумма в левой части исходной формулы тоже стремится к конечному пределу, не зависящему ни от выбора точек $z_k$, ни от выбора точек $t_k$. Предел этот называется контурным интегралом от функции $f(z)$ вдоль линии $ell$ и обозначается символом $$ intlimits_ f(z),dz=lim_ sumlimits_ ^n f(t_k)Delta z_k=intlimits_ u,dx-v,dy+ mathbf iintlimits_ v,dx+u,dy, $$ т.е. представляется как сумма криволинейных интегралов от вещественной переменной.
Обозначение для интеграла в случае замкнутой кривой: $$ ointlimits_ f(z),dz.$$
При параметрическом задании дуги $ell$: $z(s)=x(s)+iy(s)$, $s_1 0$ такое, что неравенство $|f(z)-f(z_0)| tfkp/chapter4.txt · Последние изменения: 2022/01/14 10:40 — nvr
Видео:Криволинейный интеграл по длине дуги ➜ Криволинейный интеграл 1-го родаСкачать
Интеграл по замкнутому контуру окружности
Пусть в плоскости (Oxy) задана область (R,) ограниченная замкнутой, кусочно-непрерывной и гладкой кривой (C.) Предположим, что в некоторой области, содержащей (R,) задана непрерывная векторная функция [mathbf = Pleft( right)mathbf + Qleft( right)mathbf ] с непрерывными частными производными первого порядка (largefrac > >normalsize, largefrac > >normalsize.) Тогда справедлива формула Грина [ > > — frac > >> right)dxdy> > = ] где символ (ointlimits_C ) указывает, что кривая (контур) (C) является замкнутой, и обход при интегрировании вдоль этой кривой производится против часовой стрелки.
Если (Q = x,) (P = -y,) то формула Грина принимает вид [S = iintlimits_R = frac ointlimits_C ,] где (S) − это площадь области (R,) ограниченной контуром (C.)
Формулу Грина можно записать также в векторной форме . Для этого введем понятия ротора векторного поля.
Видео:Формула Остроградского - ГринаСкачать
Интеграл по замкнутому контуру, формула Грина, примеры
Если дан криволинейный интеграл, а кривая, по которой происходит интегрирование — замкнутая (называется контуром), то такой интеграл называется интегралом по замкнутому контуру и обозначается следующим образом:
.
Область, ограниченную контуром L обозначим D. Если функции P(x, y) , Q(x, y) и их частные производные и — функции, непрерывные в области D, то для вычисления криволинейного интеграла можно воспользоваться формулой Грина:
.
Таким образом, вычисление криволинейного интеграла по замкнутому контуру сводится к вычислению двойного интеграла по области D.
Формула Грина остаётся справедливой для всякой замкнутой области, которую можно проведением дополнительных линий на конечное число простых замкнутых областей.
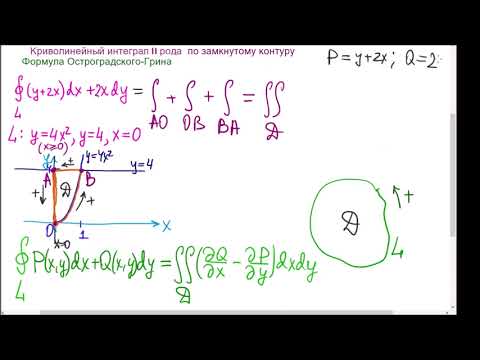
Пример 1. Вычислить криволинейный интеграл
,
если L — контур треугольника OAB , где О(0; 0) , A(1; 2) и B(1; 0) . Направление обхода контура — против часовой стрелки. Задачу решить двумя способами: а) вычислить криволинейные интегралы по каждой стороне треугольника и сложить результаты; б) по формуле Грина.
а) Вычислим криволинейные интегралы по каждой стороне треугольника. Сторона OB находится на оси Ox , поэтому её уравнением будет y = 0 . Поэтому dy = 0 и можем вычислить криволинейный интеграл по стороне OB :
Уравнением стороны BA будет x = 1 . Поэтому dx = 0 . Вычисляем криволинейный интеграл по стороне BA :
Уравнение стороны AO составим, пользуясь формулой уравнения прямой, проходящей через две точки:
.
Таким образом, dy = 2dx . Вычисляем криволинейный интеграл по стороне AO :
Данный криволинейный интеграл будет равен сумме интегралов по краям треугольника:
.
б) Применим формулу Грина. Так как , , то . У нас есть всё для того, чтобы вычислить данный интеграл по замкнутому контуру по формуле Грина:
Как видим, получили один и тот же результат, но по формуле Грина вычисление интеграла по замкнутому контуру происходит значительно быстрее.
Пример 2. Пользуясь формулой Грина, вычислить криволинейный интеграл
,
где L — контур OAB , OB — дуга параболы y = x² , от точки О(0; 0) до точки A(1; 1) , AB и BO — отрезки прямых, B(0; 1) .
Решение. Так как функции , , а их частные производные , , D — область, ограниченная контуром L , у нас есть всё, чтобы воспользоваться формулой Грина и вычислить данный интеграл по замкнутому контуру:
Пример 3. Пользуясь формулой Грина, вычислить криволинейный интеграл
, если L — контур, который образуют линия y = 2 − |x| и ось Oy .
Решение. Линия y = 2 − |x| состоит из двух лучей: y = 2 − x , если x ≥ 0 и y = 2 + x , если x .
Имеем функции , и их частные производные и . Подставляем всё в формулу Грина и получаем результат:
Пример 4. С помощью формулы Грина вычислить криволинейный интеграл
,
если L — окружность .
Решение. Функции , и их частные производные и непрерывны в замкнутом круге . Подставляем всё в формулу Грина и вычисляем данный интеграл:
Видео:Интеграл по замкнутому контуру.Без формулы ГринаСкачать
Электронная библиотека
Определение. Если функция определена на кусочно-гладкой кривой L и точки этой кривой разбивают ее на n элементарных дуг, в каждой из которых выбрана точка то , называется интегралом от f(z) по кривой L и обозначается или, в случае замкнутого контура L .
Если функция непрерывна на L, то интеграл существует (его часто называют контурным):
являются криволинейными интегралами от функций двух действительных переменных.
Если кривая L задана параметрическими уравнениями:
и каждая из этих функций гладкая, то
Известно, что вместо двух вещественных параметрических уравнений линии L можно ввести одно эквивалентное им комплексно-параметрическое уравнение
тогда уравнение (2.35) можно переписать так:
Формула (2.36) удобна для вычисления контурных интегралов.
Теорема 1 (основная теорема Коши). Если функция f(z) аналитична в односвязной области, то для любого кусочно-гладкого замкнутого контура L, лежащего в этой области,
Следствие. Если функция f(z) аналитична в односвязной замкнутой области, ограниченной кривой L, то
Заметим, что из теоремы Коши следует: если функция f(z) аналитична в односвязной области D, то для любой незамкнутой кривой L, принадлежащей D, интеграл от f(x) по L зависит только от начальной точки z0 и конечной точки z, т.е. от формы кривой (пути) L не зависит. При этом:
где F(z) – одна из первообразных функций для f(z), т.е. F’(z) = f(z). Формула (2.37) называется формулой Ньютона-Лейбница.
Теорема 2. Если функция f(z) аналитична в замкнутой области (односвязной или многосвязной) и L – граница D, то для любой точки z0, лежащей внутри этой области, справедливы следующие формулы:
Интеграл в правой части формулы (2.39) называется интегралом Коши для функции f(z), а сама эта формула носит название интегральной формулы Коши.
Формулу (2.39) часто называют интегральной формулой Коши для n-й производной функции f(z), и она выражает тот факт, что аналитическая функция, заданная в замкнутой области , дифференцируема сколько угодно раз в каждой точке z области D (следовательно, производные f’(z), f’’(z),,… аналитичны в точке z).
Отметим, что формула (2.39) получается из интегральной формулы Коши (2.38) в результате последовательного дифференцирования n раз по z0 под знаком интеграла.
Вычислить контурный интеграл где L – прямолинейный отрезок, соединяющий точку z = 0 с точкой z = 3+7i.
1) Сделаем схематический рисунок пути (контура) интегрирования (рис. 2.3).
2) 
Составим параметрические уравнения или комплексно-параметрическое уравнение пути (контура) интегрирования. Если путь интегрирования состоит из прямолинейных участков, то целесообразно использовать формулу для прямой, проходящей через две заданные точки:
Из условия z = 0, следует, что
из условия z = 3+7i, следует, что
3) Установим, как изменяется параметр t при движении от точки z = 0 до точки z = 3 + 7i.
При z = 0 у нас х = 0 и у = 0, а значит, из параметрических уравнений t = 0; при z = 3 + 7i имеем x = 3 и у = 7, тогда из тех же уравнений находим t = 1.
Таким образом, . Используем формулу (2.36):
Если путь интегрирования состоит из двух отрезков, то составляются параметрические уравнения для каждого участка отдельно и находятся два интеграла.
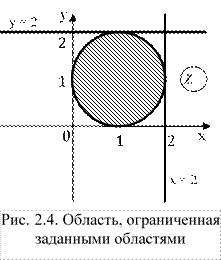
Построить область, заданную на комплексной плоскости
Запишем область в другом виде с учетом, что получим:
Это область, ограниченная окружностью с центром в точке (1, 1) и радиусом 1.
Ограничение запишем в виде:
Ограничение имеет вид:
Получили область, ограниченную графиками:
Изобразим область на графике (рис. 2.4). Заданная область заштрихована.
Найти интеграл от функции комплексного переменного, используя основную теорему Коши:
.
1) Построим область интегрирования:
Получили уравнение окружности с центром в точке О и радиусом (рис. 2.5).
2) Найдем точки и изобразим их на рисунке 2.5.
Из формулы (2.38) следует, что
Получаем, что . Точка не попадает в область интегрирования, следовательно,
1) Определяем интеграл, используя формулу (2.38):
Найти интеграл от функции комплексного переменного используя основную теорему Коши: .
Решение
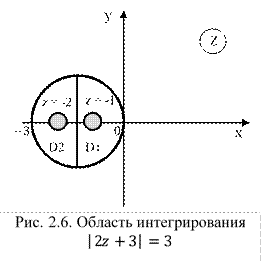
1) Построим область интегрирования:
Получили уравнение окружности с центром в точке О и радиусом (рис. 2.6).
2) Найдем точки и изобразим их на рисунке 2.6.
Из формулы (2.38) следует, что
Обе точки лежат в области интегрирования, следовательно, разбиваем область интегрирования на две замкнутые области D1 и D2. Интеграл разбиваем на два:
3) Определяем интегралы, используя формулу (2.38), найдем интеграл по области D1, где :
Найдем интеграл по области D2, где :
Складываем полученные интегралы и получаем:
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
📹 Видео
Формула ГринаСкачать
Математический анализ, 48 урок, Криволинейные интегралы второго родаСкачать
Криволинейный интеграл 1 родаСкачать
Криволинейный интеграл II рода вдоль плоской кривойСкачать
ТФКП. ИНТЕГРАЛ ПО ДУГЕ ОКРУЖНОСТИ от неаналитической функции. Метод замены переменной.Скачать
ТФКП. Вычисление контурного интеграла по вычетам.Скачать
Криволинейный интеграл 1-го рода ★ Криволинейный интеграл по длине дуги ★ ∫(x+y)dsСкачать
ТФКП. Интеграл от функции комплексного переменного. Интегралы по различным путям.Скачать
ТФКП. Вычислить интеграл по замкнутому контуру. Теорема Коши о вычетах. Характер особой точки.Скачать
ТФКП. Вычисление интегралов с помощью вычетов. Теорема Коши о вычетах. Примеры решенийСкачать
Найдите массу дуги окружности ➜ Физический смысл криволинейного интеграла 1-го рода (по длине дуги)Скачать
Формула ГринаСкачать
