Зависит от того, какой треугольник.
Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
- Если треугольник прямоугольный
- Если он равнобедренный
- Если он равносторонний
- Если известна сторона и высота
- Если известны две стороны и градус угла между ними
- Если известны длины трех сторон
- Если известны три стороны и радиус описанной окружности
- Если известны три стороны и радиус вписанной окружности
- Конспект урока по математике на тему Вычисление площади треугольника(4 класс)
- «Площадь прямоугольного треугольника». 4-й класс
- Презентация к уроку
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.
Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.
Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
- Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
- Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
- Поделите все на 4.
Если известна сторона и высота
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:
Если известны длины трех сторон
- Найдите периметр. Для этого сложите все три стороны.
- Найдите полупериметр – разделите периметр на два. Запомните значение.
- Отнимите от полупериметра длину первой стороны. Запомните.
- Отнимите от полупериметра длину второй стороны. Тоже запомните.
- Отнимите от полупериметра длину третьей стороны. И ее запомните.
- Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
- Найдите квадратный корень.
Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.
Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.
Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
Конспект урока по математике на тему Вычисление площади треугольника(4 класс)
Вычисление площади треугольника
Цели: дать представление о вычислении площади треугольника; учить строить чертеж; формировать умение формулировать правило вычисления площади треугольника; закреплять умения проводить необходимые разбиения и измерения для того, чтобы вычислить площадь каждого закрашенного треугольника.
1. Математический диктант.
а) Представьте в виде суммы произведение 127 ∙ 3.
б) Представьте в виде произведения сумму 36 + 36 + 36.
в) Разложите на два равных множителя числа 16 и 81.
г) Найдите значение выражения 18 ∙ х, если х = 0.
д) При каком значении у верно равенство 14 ∙ у = 14?
е) Запишите равенство, выражающее переместительный закон умножения.
ж) Произведение чисел 25 и 248 равно 6200. Чему равно произведение чисел 248 и 25?
2. По столбу высотой 10 м взбирается улитка. За день она поднимается по столбу на 5 метров, за ночь опускается на 4 м. Сколько дней ей потребуется, чтобы подняться на вершину столба?
Решение. За первый день улитка поднимается на 5 м, а за ночь опустится на 4 м. Следовательно, за первые сутки она окажется на высоте 1 м; 5 м пройдет за 5 суток. На шестой день улитка достигнет высоты.
3. Решите задачу . В саду посадили 4 ярда яблонь по 12 яблонь в каждом ряду и 2 ряда слив по 18 слив в каждом ряду. Сколько всего деревьев посадили?
Измените вопрос задачи, чтобы она решалась так: 12 ∙ 4 – 18 ∙ 2.
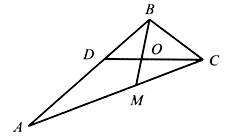
4. Назовите треугольники, у которых одной из вершин является точка А; точка О. Сколько всего треугольников на чертеже?
II. Работа по учебнику.
Задание 389. Начертите равнобедренный треугольник с основанием 6 см и высотой 4 см. Разбейте этот треугольник на два прямоугольных треугольника. Будут ли эти треугольники равны? (Будут.) Какую длину имеют катеты этих треугольников? (4 см и 3 см.) Вычислите площадь такого прямоугольного треугольника. 4 · 3 : 2 = 6 (кв. см). Вычислите площадь исходного равнобедренного треугольника. 6 · 2 = 12 (кв. см). Сравните вычисленную площадь равнобедренного треугольника с площадью прямоугольника со сторонами 6 см и 4 см.
6 · 4 = 24 (кв. см) – площадь прямоугольника со сторонами 6 см и 4 см.
24 : 12 = 2 (раза) – больше площадь прямоугольника, чем площадь равнобедренного треугольника.
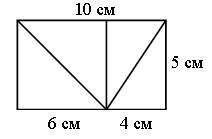
Задание 390. Рассмотрите чертеж в учебнике. Проведите в каждом из двух прямоугольников диагонали так, чтобы они имели общую вершину.
– Сравните площади исходного прямоугольника и треугольника, сторонами которого являются эти диагонали. Проведите необходимые измерения и вычислите площадь данного прямоугольника. S □ = 10 · 5 = 50 (кв. см). Вычислите площадь каждого из построенных прямоугольных треугольников.
S 1Δ = 6 · 5 : 2 = 15 (кв. см) S 2 Δ = 64 · 5 : 2 = 150 (кв. см)
– Вычислите площадь треугольника, составленного из этих прямоугольных треугольников. S = 15 + 10 = 25 (кв. см).
– Во сколько раз больше площадь прямоугольника, чем площадь треугольника? 50 : 25 = 2 (раза)
Задание 391. Прочитайте высказывания в учебнике. Какие из них можно применить для вычисления площади треугольника, у которого известны длина основания и длина высоты, проведенной к этому основанию?
• Длину основания нужно умножить на половину длины высоты.
• Половину длины основания нужно умножить на длину высоты.
• Длину основания умножить на длину высоты, а полученный результат разделить пополам.
– Вычислите площадь треугольника, у которого длина основания 8 см, а длина соответствующей высоты 5 см.
8 · 5 : 2 = 20 (кв. см).
Задание 392. Проведите необходимые разбиения и измерения для того, чтобы вычислить площадь каждого закрашенного треугольника.
«Площадь прямоугольного треугольника». 4-й класс
Класс: 4
Презентация к уроку
Тип урока: урок введения нового знания.
Цель урока:
- познакомить с алгоритмом нахождения площади прямоугольного треугольника;
- учить находить площадь прямоугольного треугольника по его катетам;
- развивать логическое мышление, речь и память учащихся;
- воспитывать аккуратность в выполнении чертежей и уважение к товарищам.
Планируемый результат:
- знать формулу нахождение площади прямоугольного треугольника;
- уметь находить S прямоугольного треугольника по его катетам.
Основные понятия: прямоугольный треугольник, площадь прямоугольного треугольника.
Межпредметные связи: геометрия, окружающий мир.
Оборудование:
- Учебник Математика 4 класс, часть 1, урок 38. Т.Е. Демидова, С. А, Козлова, А.П.Тонких.
- Карточки “Математическое лото”.
- Презентация.
| Ход урока | Комментарий |
| 1. Организационный момент. Слайд 1. |
— Сегодня нам с вами предстоит сделать новое открытие. Но прежде чем это произойдет, давайте немного повторим пройденный материал.
— Хлопните столько раз, сколько геометрических фигур вы видите.
— Присядьте за парту столько раз, сколько получится в результате вычисления в данной цепочке.
Запись даты в тетрадях.
2. Актуализация опорных знаний.
А) Индивидуальная работа (работа по карточкам).
| 5000 + 6000 | 10 000 — 3000 | 11000 + 16000 |
| 32000 — 19000 | 24050 + 900 | 457300 + 40 |
| 165720 — 700 | 4 870 640 — 870 000 |
Б) Работа с таблицами на доске.
Проанализируйте зависимость между переменными х и у, назовите формулы.
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| у | 1 | 4 | 9 | 16 | 25 |
Рассмотрите следующую таблицу, сравните её с первой.
| х | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| у | 4 | 7 | 12 | 19 | 28 | 39 |
(Значения х равны, а значения у увеличились на 3)
— Запишите формулу. Заполните таблицу.
Что такое формулы? Слайд 3.
(Формулы – это верные равенства, устанавливающие взаимосвязь между величинами)
Цель: повторение изученного материала, необходимого для “открытия нового знания”, и выявление затруднений в индивидуальной деятельности каждого учащегося.
— Повторим математические формулы. Играем в математическое лото.
(7 учеников до урока получили карточки на картоне. Каждая карточка состоит из двух частей – слева свой ответ, справа – вопрос для другого ученика. Первым начинает задавать вопрос тот ученик, у которого справа на карточке написан только вопрос. Другой ученик, у которого на карточке есть ответ на этот вопрос, встаёт и отвечает. Весь класс слушает и хлопает в ладоши в случае правильного ответа. Ответив, ученик читает вопрос с правой стороны своей карточки. Отвечает следующий ученик, карточка которого начинается с этого ответа. Так по цепочке играют до последнего ответа. Последним играет ученик, у которого на карточке слева есть только ответ, но нет следующего вопроса.)
| Формула деления с остатком. | |
| a = b * с + r | Формула расстояния. |
| s = v * t | Формула периметра прямоугольника. |
| Р = (а + b) * 2 | Формула времени. |
| t = s : v | Формула периметра квадрата. |
| P = (a + a) * 2 | Формула объёма прямоугольного параллелепипеда. |
| V = a * b * c | Формула площади квадрата. |
| S = a * a | Формула скорости. |
| v = s : t | Формула периметра треугольника. |
| P = a + b + c | Формула площади прямоугольника. |
| S = a * b |
Разделите формулы на группы.
Какая формула может быть “лишней”? Почему?
Физминутка. Зарядка для глаз.
Рисуй глазами треугольник.
Теперь его переверни
Вершиной вниз.
И вновь глазами
Ты по периметру веди.
Рисуй “восьмёрку” вертикально
Ты головою не крути,
А лишь глазами осторожно
Ты вдоль по линиям води,
И на бочок её клади.
Теперь следи горизонтально,
И в центре ты остановись.
Зажмурься крепко, не ленись
Глаза мы открываем, наконец.
Г) Прочитайте стихотворение. Слайд 4.
Попарно три прямых, пересекаясь,
Мне к трём углам дают три стороны.
По – разному всегда я называюсь,
Когда углы иль стороны даны.
Коль остры все углы, — и я остроуголен.
С одним тупым – тупоуголен.
Коль остры два, третий – прям –
Прямоуголен я.
По сторонам бываю я равносторонним,
Когда все стороны равны.
Когда ж все разные даны,
То я зовусь разносторонним.
И если, наконец, равны две стороны,
Равнобедренным я величаюсь.
- Какие бывают треугольники по сторонам? (равносторонние, разносторонние, равнобедренные).
- Какие бывают треугольники по углам? (остроугольные, тупоугольные, прямоугольные).
- Какая фигура “лишняя”? Почему? (прямоугольник, 4 стороны, 4 угла)
Рассмотрите фигуры. Слайд 6.
— Как называются данные фигуры?
(Квадрат, прямоугольник, прямоугольный треугольник).
— Для каждой фигуры запишите формулы нахождения площади. Дети самостоятельно записывают в тетрадях формулы. Задание по рядам.
— Смогли ли вы полностью выполнить задание?
Сегодня мы с вами выведем формулу площади прямоугольного треугольника. Давайте подумаем, можно ли составить формулу площади прямоугольного треугольника?
— На партах модель прямоугольника АВСД.
— Измерьте стороны прямоугольника. (5 см и 4см).
— Найдите площадь прямоугольника. (20 см 2 ).
— Проведите диагональ АС.
— Разрежьте прямоугольник по диагонали. Что получилось?
— Что вы можете сказать по поводу этих треугольников? (Они равны).
— Докажите, что треугольники равны. (Метод наложения).
— Какие углы образует треугольник?
— Как вы назовете данные треугольники? (Прямоугольный).
Работа по учебнику. С. 94, !.
— Что нового узнали о прямоугольном треугольнике? (Две стороны, образующие прямой угол называются катетами, а третья – гипотенуза).
— Имеют треугольники площадь? (да)
— Как узнать площадь прямоугольного треугольника? (Дети должны сами найти решение: треугольник составляет половину прямоугольника; если площадь прямоугольника а * в, то площадь прямоугольного треугольника равна (а * в) : 2)
— Подумайте, как нужно изменить формулу площади прямоугольника, чтобы получилась формула площади прямоугольного треугольника? (Дети самостоятельно пишут в тетради)
— Проверяем. Трое учеников выходят к доске и пишут свою формулу. Потом все обсуждают, кто написал верно.
— Итак, площадь вашего прямоугольного треугольника зависит от площади прямоугольника.
5. Первичное закрепление.
Работа по учебнику. С. 95 № 7 ( а )
S тр. = 30мм x 40мм
S тр. = 1200 мм кв.
Цель: решение устных задач и обсуждение проекта решения.
— Найдите площадь прямоугольного треугольника.
7. Включение нового знания в систему знаний и повторение.
Работа по учебнику. С. 95, № 7.
Задания под буквами б, в – обязательные для выполнения. Задания обозначенные точками по желанию.
Во время работы слабоуспевающим детям помогают консультанты.
— Может ли площадь прямоугольного треугольника, полученного при проведении диагонали в прямоугольнике, быть больше площади данного прямоугольника?
— В каком отношении находятся площади данных фигур?
(Площадь прямоугольного треугольника равна половине значения произведения сторон, образующих прямой угол).
— Составляем дерево успеха.
- Зеленый листок – не допустил ни одной ошибки, доволен собой;
- Желтый листок – допустил неточность;
- Красный листок – надо постараться и успех будет!
Домашнее задание. Слайд 12,13,14.
Учебник с.95 свед. № 7 (б.г), № 9 (1 ст).
Цель: каждый для себя должен сделать вывод о том, что он уже умеет.