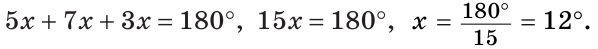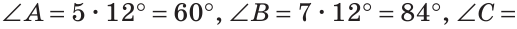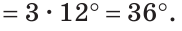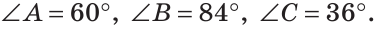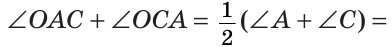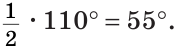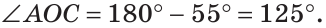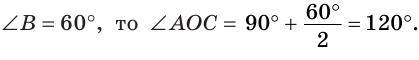Сумма углов треугольника:
Великий французский ученый XVII в. Блез Паскаль (1623—1662) еще в детстве любил изучать геометрические фигуры, открывать их свойства, измерять углы транспортиром.
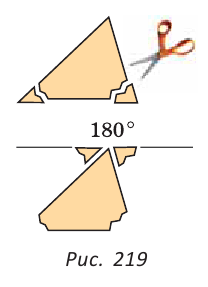
Юный исследователь заметил, что у любого треугольника сумма углов одна и та Ж6 180°. «Как же это объяснить?» — думал Паскаль. Тогда он отрезал у треугольника два уголка и приложил их к третьему (рис. 219). Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие! Дальнейшая судьба мальчика была предопределена.
Теорема. Сумма углов треугольника равна 180°.
Дано: 
Доказать: 
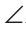
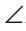
Доказательство:
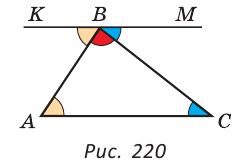
Через вершину В треугольника ABC проведем прямую КМ, параллельную стороне АС. Тогда 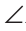
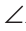





Следствия.
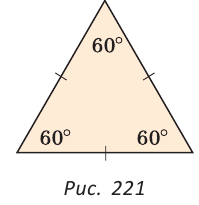
1. Каждый угол равностороннего треугольника равен 60°. (рис. 221).
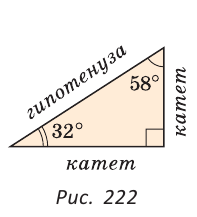
2. Сумма острых углов прямоугольного треугольника равна 90° (рис. 222).
В прямоугольном треугольнике стороны, заключающие прямой угол, называются катетами, сторона, противолежащая прямому углу, — гипотенузой (см. рис. 222).
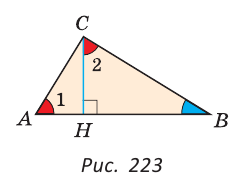
Проведем в прямоугольном треугольнике ABC высоту СН к гипотенузе АВ (рис. 223). Так как в треугольнике ABC угол 1 дополняет угол В до 90°, а в треугольнике СНВ угол 2 также дополняет угол В до 90°, то
Доказано свойство: «Угол между высотой прямоугольного треугольника, проведенной к гипотенузе, и катетом равен углу между другим катетом и гипотенузой».
Пример:
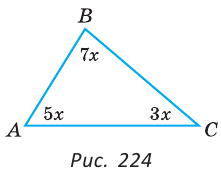
В треугольнике ABC градусные меры углов А, В и С относятся соответственно как 5:7:3. Найти углы треугольника (рис. 224).
Решение:
Пусть 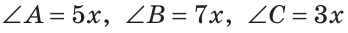
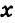
Так как сумма углов треугольника равна 180°, то
Тогда
Ответ:
Пример:
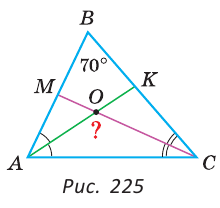
В треугольнике ABC (рис. 225) угол В равен 70°, АК и СМ — биссектрисы, О — точка их пересечения. Найти угол АОС между биссектрисами.
Решение:
Сумма углов А и С треугольника ABC равна 180° — 70° = 110°. Так как биссектриса делит угол пополам, то
Из треугольника АОС находим:
Замечание. Если 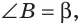
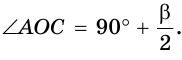
Пример:
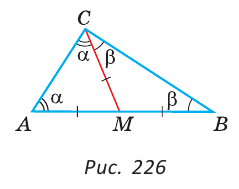
Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то данный треугольник — прямоугольный.
Доказательство:
Пусть СМ — медиана, 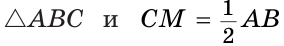
Докажем, что























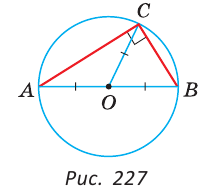
Замечание. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. На рисунке 227 это угол АСВ. Из задачи 3 следует свойство: «Вписанный угол, опирающийся на диаметр, — прямой».
Пример:
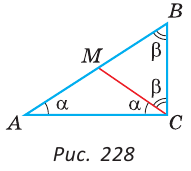
Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство:
Пусть в треугольнике ABC (рис. 228) 




Проведем отрезок СМ так, что










| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Градусная мера углаСкачать
Остроугольный, прямоугольный и тупоугольный треугольники.
Виды треугольников
Остроугольный треугольник — это треугольник,
в котором все углы острые.
Прямоугольный треугольник — это треугольник,
в котором один из углов прямой.
Тупоугольный треугольник — это треугольник,
в котором один из углов тупой.
Как определить вид треугольника
Для того, чтобы понять какой треугольник — остроугольный, прямоугольный или тупоугольный
нужно знать какая градусная мера у углов в треугольнике.
Если один из углов в треугольнике прямой, значит треугольник прямоугольный. Все углы острые в треугольнике — значит треугольник остроугольный. Если в треугольнике один из углов тупой, значит треугольник тупоугольный.
В произвольном треугольнике все углы острые, или два угла острые, а третий прямой или тупой. Если в треугольнике вам известно, что один углов тупой или прямой, значит сумма двух других углов не больше 90 градусов.
В прямоугольном треугольнике стороны напротив острых углов называются катетами, а сторона напротив прямого угла называется гипотенузой.
Градусные меры острого, тупого, прямого углов в треугольниках
Чтобы понять как называется угол и как называется треугольник с этими углами — надо знать его градусную меру:
- Острый угол в любом из треугольников не больше 90 градусов.
- Прямой угол в любом из треугольников равен 90 градусам.
- Тупой угол в любом из треугольников больше 90 градусов, но меньше 180 градусов.
Видео:7 класс, 9 урок, Градусная мера углаСкачать

Углы. Градусная мера угла.
Мерой угла является размер поворота луча около точки как центра вращения.
Что такое градусная мера угла? Градусной мерой угла является число больше нуля, которое показывает,
какое число раз градус и его части — минута и секунда — помещаются в этом угле, т.е. градусная мера —
величина, которая отражает число градусов, минут и секунд между двумя сторонами угла.
У любого угла существует определенная градусная мера, которая больше 0. Развернутый угол = 180°.
Градусная мера угла соответствует сумме градусных мер углов, разбиваемый всяким лучом, который
проходит между его сторонами.
От всякого луча в необходимую полуплоскость есть возможность отложить угол с необходимой градусной
мерой, меньше чем 180°, и только 1.
Мерой плоского угла, который является элементом полуплоскости, является градусная мера угла с теми же
сторонами. Мерой плоского угла, который содержит полуплоскость, является величина 360° – α ,
где α – градусная мера дополнительного плоского угла.
2 угла будут называться равными, когда их градусные меры одинаковы.
Так же как при делении часа, как интервала времени, градус делится на 60 минут — минуты обозначается
знаком ‘, а минуту — на 60 секунд — обозначается знаком ».
Свойства углов.
- У любого угла есть определенная градусную меру, большая нуля. Развернутый угол = 180°.
- Градусная мера угла соответствует сумме градусных мер углов, разбиваемый всяким лучом,
который проходит меж его сторонами.
- От всякого луча в необходимую полуплоскость есть возможность отложить угол с данной градусной
мерой, меньше чем 180°, и только один.
Как найти градусную меру угла?
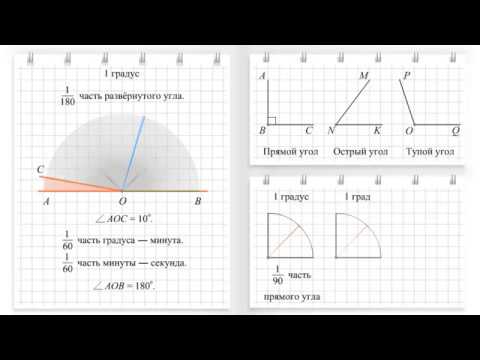
1 градус (°) — это угол, равный 1/180 части развернутого угла. Если выразиться по другому, если возьмем
развернутый угол и поделим его на 180 одинаковых меж собой частей-углов, то любой такой маленький угол
будет соответствовать 1 градусу. Размер остальных углов вычисляется тем, какой число этих маленьких
углов возможно разместить внутри угла, который измеряется.
Т.о., развернутый угол = 180°, прямой угол = 90°, острые углы меньше, чем 90°, а тупые — больше,
Если угол невозможно измерить точно в целых градусах, то не обязательно использовать минуты и секунды.
Можно пользоваться дробными значениями градуса. Например, 96,5°.
Известно, что минуты и секунды легко переводятся в градусы, выражая их в долях градуса.
Например, 30′ = (30/60)° или 0,5°. А 0,3° = (0,3 * 60)’ или 18′. Т.о., пользоваться минутами и секундами —
📺 Видео
7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Угол. Градусная мера угла. 5 класс.Скачать

Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать

9. Градусная мера углаСкачать
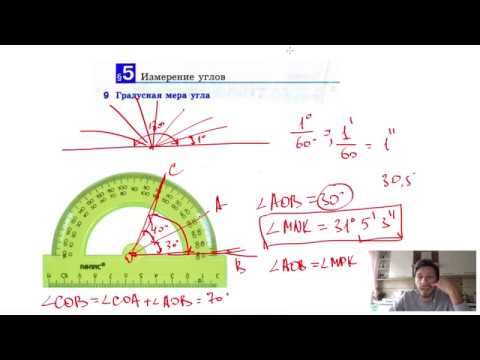
Измерение угла с помощью транспортираСкачать

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Геометрия 7 класс (Урок№23 - Сумма углов треугольника.)Скачать

Построение углов заданной градусной мерыСкачать

Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

№224. Найдите углы треугольника ABC, если ∠A:∠B:∠C= 2:3:4.Скачать

Углы треугольника относятся как 2:3:4. Найдите их градусные мерыСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Внешний угол треугольникаСкачать

КАК ИЗМЕРИТЬ УГЛЫ ТРЕУГОЛЬНИКА ТРАНСПОРТИРОМ? Примеры | МАТЕМАТИКА 5 классСкачать

Геометрия 7 класс (Урок№5 - Измерение углов.)Скачать

Задача про градусную меру углов. Геометрия 7 класс.Скачать

Градусная мера угла. 9 класс.Скачать

Угол. 7 класс.Скачать