Взаимно перпендикулярные углы треугольника

Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

Теорема об углах с соответственно перпендикулярными сторонами

Теорема

Дано: АОВ, А₁О₁В₁, ОАО₁А₁, ОВО₁В₁.

Доказать: АОВ = А₁О₁В₁ или АОВ + А₁О₁В₁ = 180 0 .

Доказательство:

1 случай

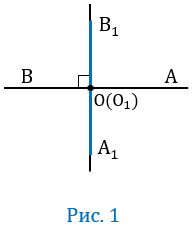
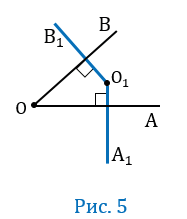
Пусть угол АОВ — развернутый (Рис. 1).

Угол АОВ — развернутый, значит лучи ОА и ОВ будут лежать на одной прямой, при этом по условию ОАО₁А₁, ОВО₁В₁, значит, лучи О₁А₁ и О₁В₁ также будут лежать на одной прямой, следовательно, А₁О₁В₁ — будет развернутым, тогда АОВ = А₁О₁В₁.

2 случай

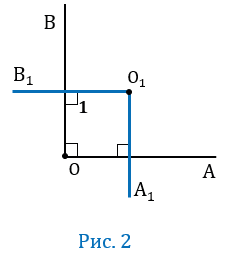
Пусть угол АОВ — прямой, т.е. равен 90 0 (Рис.2).

АОВ = 90 0 , то ОАОВ, при этом по условию ОАО₁А₁, следовательно, ОВО₁А₁. Итак, О₁В₁ — секущая относительно прямых ОВ и О₁А₁, ОВО₁А₁, тогда по теореме об односторонних углах их сумма равна 180 0 , т.е. 1 + А₁О₁В₁ = 180 0 , откуда А₁О₁В₁ = 180 0 —1, при этом по условию ОВО₁В₁, значит 1 — прямой, т.е. 1 = 90 0 , следовательно, А₁О₁В₁ = 180 0 — 90 0 = 90 0 . Из равенств АОВ = 90 0 и А₁О₁В₁ = 90 0 следует, что АОВ = А₁О₁В₁ и АОВ + А₁О₁В₁ = 90 0 + 90 0 = 180 0 .

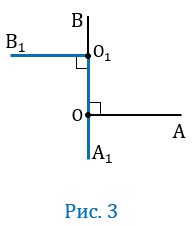
3 случай

Пусть ОО₁А₁ (Рис.3).

По условию ОО₁А₁, тогда лучи ОВ и О₁А₁ будут лежать на одной прямой А₁В. По условию ОАО₁А₁, ОВО₁В₁, значит, ОА и О₁В₁ будут перпендикулярны одной прямой А₁В, следовательно, ОАО₁В₁. Итак, ОАО₁В₁, А₁В — секущая относительно прямых ОА и О₁В₁, тогда по теореме о накрест лежащих углах АОВ = А₁О₁В₁, причем, учитывая то, что ОАО₁А₁, ОВО₁В₁ эти углы будут прямые, т.е. АОВ = А₁О₁В₁ = 90 0 , тогда АОВ + А₁О₁В₁ = 90 0 + 90 0 = 180 0 .

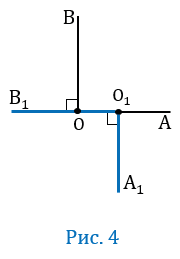
4 случай

Пусть ОО₁В₁ (Рис.4).

По условию ОО₁В₁, тогда лучи ОА и О₁В₁ будут лежать на одной прямой В₁А. По условию ОАО₁А₁, ОВО₁В₁, значит ОВ и О₁А₁ будут перпендикулярны одной прямой В₁А, следовательно, ОВО₁А₁. Итак, ОВО₁А₁, В₁А — секущая относительно прямых ОВ и О₁А₁, тогда по теореме о накрест лежащих углах АОВ = А₁О₁В₁, причем, учитывая то, что ОАО₁А₁, ОВО₁В₁ эти углы будут прямые, т.е. АОВ = А₁О₁В₁ = 90 0 , тогда АОВ + А₁О₁В₁ = 90 0 + 90 0 = 180 0 .

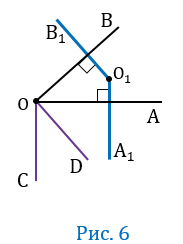
5 случай

Пусть угол АОВ — острый, т.е. меньше 90 0 , при этом ОО₁А₁, ОО₁В₁ (Рис.5).

Проведем луч ОС так, чтобы прямые ОА и ОС были взаимно перпендикулярными (т.е. ОАОС), а точки В и С лежали по разные стороны от прямой ОА. Далее проведем луч ОD так, чтобы прямые ОВ и ОD были взаимно перпендикулярными (т.е. ОВОD), а точки С и D лежали по одну сторону от прямой ОА (Рис.6).

Получим, что АОВ = 90 0 — АОD, а СОD = 90 0 — АОD, значит АОВ = СОD. Стороны угла СОD соответственно параллельны сторонам угла А₁О₁В₁, т.е. ОСО₁А₁ (т.к. две прямые перпендикулярные к третьей прямой параллельны друг другу, по построению ОАОС и по условию ОАО₁А₁), также ОDО₁В₁ (т.к. по построению ОВОD и по условию ОВО₁В₁), поэтому по теореме об углах с соответственно параллельными сторонами либо СОD = А₁О₁В₁, либо СОD + А₁О₁В₁ = 180 0 . Следовательно, учитывая то, что АОВ = СОD получим, либо АОВ = А₁О₁В₁, либо АОВ + А₁О₁В₁ = 180 0 .

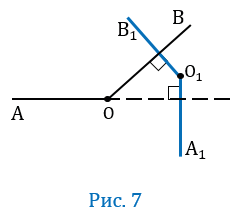
6 случай

Пусть угол АОВ — тупой, т.е. меньше 180 0 , но больше 90 0 , при этом ОО₁А₁, ОО₁В₁ (Рис.7).

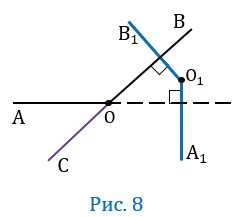
Проведем луч ОС так, чтобы угол АОС был смежным с углом АОВ (Рис.8).

Угол АВС острый, и его стороны соответственно перпендикулярны сторонам угла А₁О₁В₁. Следовательно, либо АОС + А₁О₁В₁ = 180 0 , либо АОС = А₁О₁В₁ (смотри случай 5). Тогда, учитывая, что углы АОС и АОВ смежные, их сумма будет равна 180 0 , значит АОС = 180 0 — АОВ, следовательно, в первом случае 180 0 — АОВ + А₁О₁В₁ = 180 0 , откуда АОВ = А₁О₁В₁, а во втором случае 180 0 — АОВ = А₁О₁В₁, откуда АОВ + А₁О₁В₁ = 180 0 . Что и требовалось доказать.

Поделись с друзьями в социальных сетях:

Видео:Перпендикулярные прямые. 6 класс.Скачать

Углы с соответственно перпендикулярными сторонами равны между собой, если они оба острые или оба тупые.

21.04.2020

Углы со взаимно перпендикулярными и взаимно параллельными сторонами.

Углы с соответственно параллельными сторонами.

Возьмём на плоскости две точки С и О и из этих точек проведём две пары лучей
СА || ОМ и СВ || ОN так, чтобы углы АСВ и МОN были или оба острые (рис. 1), или оба тупые (рис. 2).

Рис. 1

Рис. 2

Углы АСВ и МОN— углы с соответственно параллельными cторонами. Докажем, что эти углы равны между собой.

Пусть СВ пересекает ОМ в точке D. , как соответственные углы при параллельных АС и МО и секущей СВ.

, как соответственные углы при параллельных СВ и ОN и секущей МО, но тогда и .

Следовательно, углы с соответственно параллельными сторонами равны, если они оба острые или оба тупые.

Рис.3

Построим два острых угла АСВ и МОN с соответственно параллельными сторонами (рис. 3): СА || МО и СВ || ОN, и продолжим за вершину О стороны угла МОN. При вершине О образовались два тупых угла ЕОМ и FОN (так как смежный с ними угол МОN по построению острый). Каждый из них в сумме с углом МОN составляет 2d, а так как , то и .

Следовательно , углы с соответственно параллельными сторонами в сумме составляют 2d, если один из них острый, а другой тупой.

Углы с соответственно перпендикулярными сторонами.

Рис. 4	Построим произвольный острый угол АВС. Проведём через вершину угла лучи, перпендикулярные к его сторонам, так, чтобы они образовали острый угол. BO_|_ ВС и ВК _|_ АВ (рис. 4). Мы получим новый угол OBK. Стороны углов AВС и ОВК взаимно перпендикулярны. / АВС = d — / СВК; / ОВК = d — / СВК. Отсюда следует, что / АBС = / ОВК.
Построим произвольный тупой угол АОВ и через его вершину проведём лучи, перпендикулярные к его сторонам, так, чтобы они образовали тупой угол. ОК_|_ОА и ОС_|_ОВ (рис. 5), угол КОС — тупой. Стороны углов АОВ и КОС взаимно перпендикулярны, поэтому / АОВ = d + / КОВ; / КОС = d + / КОВ. Отсюда следует, что / АОВ = / КОС.	Рис. 5

Углы с соответственно перпендикулярными сторонами равны между собой, если они оба острые или оба тупые.

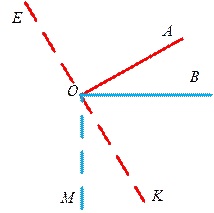Рис. 6

Построим произвольный острый угол АОВ и проведём через его вершину перпендикуляры к его сторонам так, чтобы они образовали острый угол (рис. 6). Получим: / КОМ = / АОВ. Продолжим сторону ОК за вершину О. Стороны угла ЕОМ перпендикулярны сторонам угла АОВ. При этом / ЕОМ — тупой, так как смежный с ним / МОК — острый. / КОМ + / ЕОМ = 2d (как углы смежные). Но / КОМ по ранее доказанному равен / АОВ. Следовательно, и / АОВ + / ЕОМ = 2d.

Углы с соответственно перпендикулярными сторонами в сумме составляют 2d, если один из них острый, а другой тупой.

Мы рассматривали углы, составленные взаимно перпендикулярными сторонами, когда они имели общую вершину. Выведенные нами свойства будут справедливы и в том случае, когда углы не будут иметь общей вершины.

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Please wait.

Видео:Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

We are checking your browser. mathvox.ru

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Эксперт (Короткометражка, Русский дубляж)Скачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6dad64168dae1610 • Your IP : 85.95.188.35 • Performance & security by Cloudflare

🌟 Видео

Геометрия 7 класс. Углы с соответственно параллельными или перпендикулярнымСкачать

Перпендикулярные прямыеСкачать

Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Геометрия 7 класс (Урок№7 - Перпендикулярные прямые.)Скачать

7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

7 класс, 12 урок, Перпендикулярные прямыеСкачать

82 Углы с соответственно перпендикулярными сторонами (150)Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

УГЛЫ СО ВЗАИМНО-ПЕРПЕНДИКУЛЯРНЫМИ СТОРОНАМИ #calculus #maths #огэ #егэ #algebra #школа #физикаСкачать

Наклонная, проекция, перпендикуляр. 7 класс.Скачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Как построить две взаимно перпендикулярные прямые с помощью циркуляСкачать

№211. Плоскости правильного треугольника KDM и квадрата KMNP взаимно перпендикулярны. Найдите DN, есСкачать