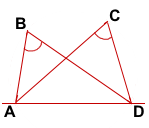
Признак принадлежности четырёх точек одной окружности
Если точки B и C лежат в одной полуплоскости относительно прямой AD, и точки B и C видны из отрезка AD под одним углом (то есть ∠ABD=∠ACD), то точки A, B, C и D лежат на одной окружности.
Дано: точки B и C лежат в одной полуплоскости относительно прямой AD,
Доказать: точки A, B, C, D лежат на одной окружности
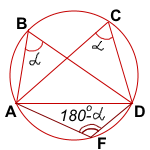
Опишем около треугольника ABD окружность.
Отметим на этой окружности произвольную точку F, лежащую относительно прямой AD в другой полуплоскости, чем точки B и C.
Четырёхугольник ABDF — вписанный в окружность. Следовательно, сумма его противолежащих углов равна 180°:
Рассмотрим четырехугольник ACDF.
Отсюда следует, что четырёхугольник ABDF — вписанный.
Поскольку около треугольника ABD можно описать только одну окружность, то точка C лежит на той же окружности, что и точки A, B и D.
Видео:Досрочный ОГЭ Математика. Задание 17 (1 вариант).Скачать

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2
Вступление
Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.
Начнем с взаимного расположения точки относительно прямой, луча и отрезка.
Задача №1
Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.
Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P1(x1, y1), P2(x2, y2). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P1P2 и P1M и по его знаку сделать вывод.
Задача №2
Определить принадлежит ли точка лучу.
Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P1(x1, y1) — начало луча, а P2(x2, y2) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P1(x1, y1), где P2(x2, y2) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (P1P2, P1M) ≥ 0 – скалярное произведение (точка лежит на луче)
Задача №3
Определить принадлежит ли точка отрезку.
Решение
Пусть точки P1(x1, y1), P2(x2, y2) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P1, P2. Далее нам нужно определить лежит ли точка между точками P1 и P2, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP1, MP2). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P1(x1, y1), P2(x2, y2) необходимо и достаточно выполнения условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (MP1,MP2) ≤ 0 – скалярное произведение (точка лежит между P1 и P2)
Задача №4
Взаимное расположение двух точек относительно прямой.
Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.
Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P1P2, P1M1] * [P1P2, P1M2] 0 – точки лежат по одну сторону.
3. [P1P2, P1M1] * [P1P2, P1M2] = 0 – одна (или две) из точек лежит на прямой.
Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P1P2, P1M1] * [P1P2, P1M2] ≤ 0.
Задача №5
Определить пересекаются ли две прямые.
Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a1x + b1y + c1 = 0 и a2x + b2y + c2 = 0. Тогда условие параллельности прямых заключается в том, что a1b2 — a2b1 = 0.
Если же прямые заданы точками P1(x1, y1), P2(x2, y2), M1(x3, y3), M2(x4, y4), то условие их параллельности заключается в проверки косого произведения векторов P1P2 и M1M2: если оно равно нулю, то прямые параллельны.
В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b1, a1), (-b2, a2) которые называются направляющими векторами.
Задача №6
Определить пересекаются ли два отрезка.
Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:
Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P1P2, P1M2] > 0, [P1P2, P1M1] [P1P2, P1M2] * [P1P2, P1M1] 2 + b 2 ).
Задача №8
Расстояние от точки до луча.
Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.
В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.
Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP1P2 – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
1. (P1M, P1P2) 2 .
Теперь рассмотрим случай, когда центр второго круга O2 находится между точками O1 и C. В этом случае получим отрицательное значение величины d2. Использование отрицательного значения d2 приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.
Заключение
Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.
Видео:Треугольник АВС вписан в окружность с центром в точке О. Точки О и С лежат в одной полуплоскости...Скачать

Разные полуплоскости относительно прямой в окружности
Проведём на плоскости какую-нибудь прямую а. Она разобьёт плоскость на две части. На рисунке 8.1 точки А и В принадлежат одной из этих частей, отрезок АВ не пересекает прямую. В этом случае говорят также, что точки А и В лежат по одну сторону от прямой а. Точки В и С принадлежат разным частям плоскости, отрезок ВС пересекает прямую а. В этом случае говорят также, что точки В и С лежат по разные стороны от прямой а.
Следующее свойство является аксиомой взаимного расположения точек на плоскости относительно данной прямой.
• Каждая прямая на плоскости разбивает эту плоскость на две части. При этом если две точки принадлежат разным частям , то отрезок, соединяющий эти точки, пересекается с прямой. Если две точки принадлежат одной части, то отрезок , соединяющий эти точки, не пересекается с прямой.
Часть плоскости, состоящая из точек данной прямой и точек, лежащих по одну сторону от этой прямой, называется полуплоскостью (рис. 8.2).
1. На сколько частей прямая разбивает плоскость?
2. Что называется полуплоскостью?
3. В каком случае две точки принадлежат: а) одной полуплоскости; б) разным полуплоскостям относительно данной прямой?
1. Изобразите прямую/? и точки А, В, С , D, Е, Е такие, что А, Е принадлежат данной прямой, а остальные ей не принадлежат, причём D и У лежат в разных полуплоскостях, В и С — в одной полуплоскости, и отрезок BD пересекает прямую р.
2. Даны прямая и четыре точки А, В, С, D, не принадлежащие этой прямой а. Пересекает ли эту прямую отрезок AD , если: а) отрезки АВ, ВС и CD пересекают прямую а б) отрезки АС и ВС пересекают прямую а, а отрезок BD не пересекает; в) отрезки АВ и CD пересекают прямую а, а отрезок ВС не пересекает; г) отрезки АВ и CD не пересекают прямую а, а отрезок ВС пересекает; д) отрезки АВ, ВС и CD не пересекают прямую д; е) отрезки АС, ВС и BD пересекают прямую? Изобразите данные ситуации.
3. Даны пять точек и прямая, не проходящая ни через одну из этих точек. Известно, что три точки расположены в одной полуплоскости, а две другие — в другой полуплоскости относительно этой прямой. Каждая пара точек соединена отрезком. Сколько отрезков: а) пересекает прямую; 6) не пересекает прямую? Сделайте соответствующий рисунок.
4. Изобразите две пересекающиеся прямые. На сколько частей они разбивают плоскость?
5. Изобразите три прямые, пересекающиеся в одной точке. На сколько частей они разбивают плоскость?
6. Изобразите четыре прямые, пересекающиеся в одной точке. На сколько частей они разбивают плоскость?
7. На сколько частей разбивают плоскость п прямых, пересекающихся в одной точке?
8. Изобразите три попарно пересекающиеся прямые, не пересекающиеся в одной точке. На сколько частей они разбивают плоскость?
9. Изобразите четыре попарно пересекающиеся прямые, никакие три из которых не пересекаются в одной точке. На сколько частей они разбивают плоскость?
10*. На сколько частей разбивают плоскость п попарно пересекающихся прямых, никакие три из которых не пересекаются в одной точке?
🎬 Видео
№147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВССкачать
Уравнение окружности (1)Скачать

ОГЭ по математике. Треугольник вписан в окружность . (Вар. 4) √ 17 модуль геометрия ОГЭСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

2034 треугольник ABC вписан в окружность с центром в точке O точки O и C лежат в одной полуплоскостиСкачать

Треугольник АВС вписан в окружность с центром в точке О. Точки О и С лежат в одной #shortsСкачать

🔴 В окружности с центром O отрезки AC и BD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Нахождение точки, симметричной данной относительно плоскости в пространствеСкачать

На окружности по разные стороны от диаметра AB ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Симметрия относительно прямойСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

ОКРУЖНОСТЬ (признак принадлежности четырех точек одной окружности) ЧАСТЬ 4Скачать

Поступающим в магистратуру МГУ, математика, 2018 год, первая волна, задача 1 (1)Скачать

Треугольник ABC вписан в окружность с центром O Угол BAC равен 32°Скачать

Повторение изученного в 7 классе Геометрия все темы просто! Видеоурок. Вся геометрия в одном урокеСкачать

10 класс, 11 урок, Числовая окружностьСкачать