Страницы работы
Содержание работы
Вычертить контуры деталей,применяя правила построения сопряжений и деления окружностей на равные части,нанести размеры.
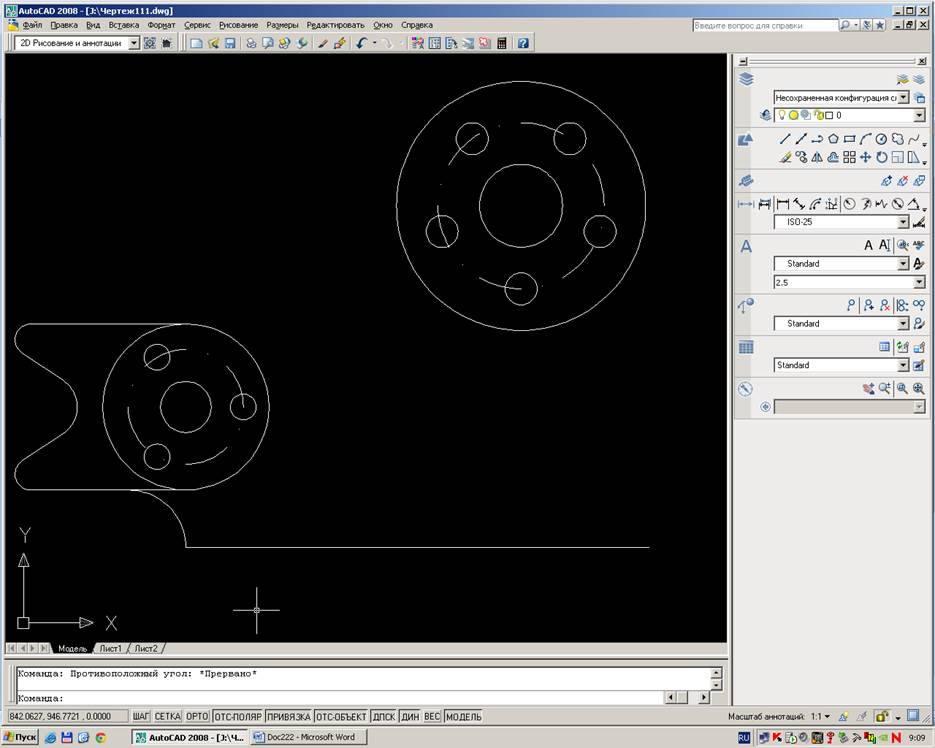
1. Начинаем с построения окружностей левой части корпуса,при этом применяем функцию Массив для построения внутренних окружностей.
2.От наружней окружности рисуем отрезки длиной 65 мм. Сверху и снизу,затем отрезки соединяем с центром внешнего радиуса наружней окружности.Затрем используем функцию Сопряжение и делаем три сопряжения два R5 и одно R10.
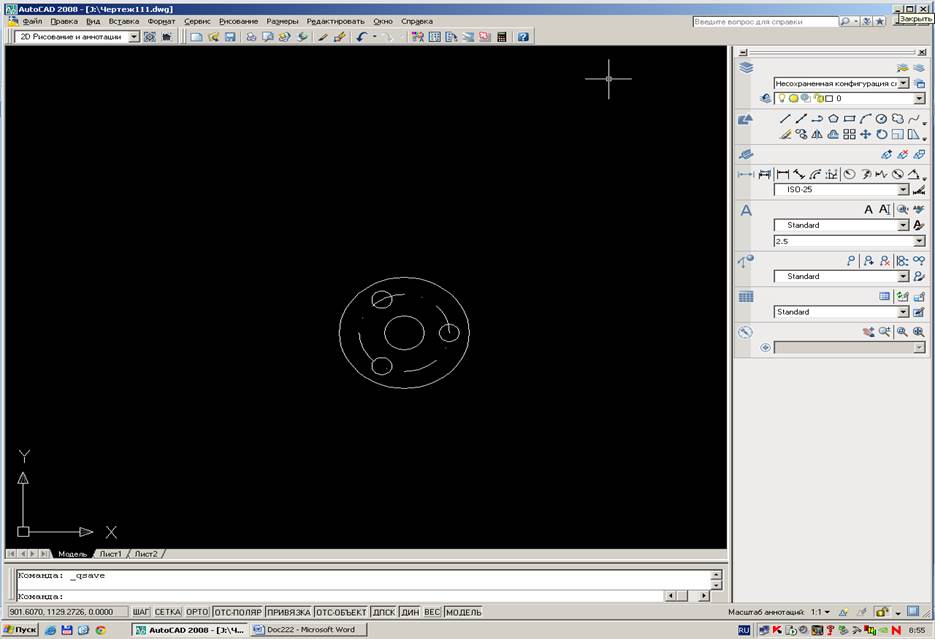
3.В нижней части окружности проводим ещё одно сопряжение R18 с линией,находящейся на расстоянии 18мм ниже.
4.Чертим правые окружности,при этом используя функцию Массив для нанесения на чертёж 5-ти окружностей диаметром 10мм.
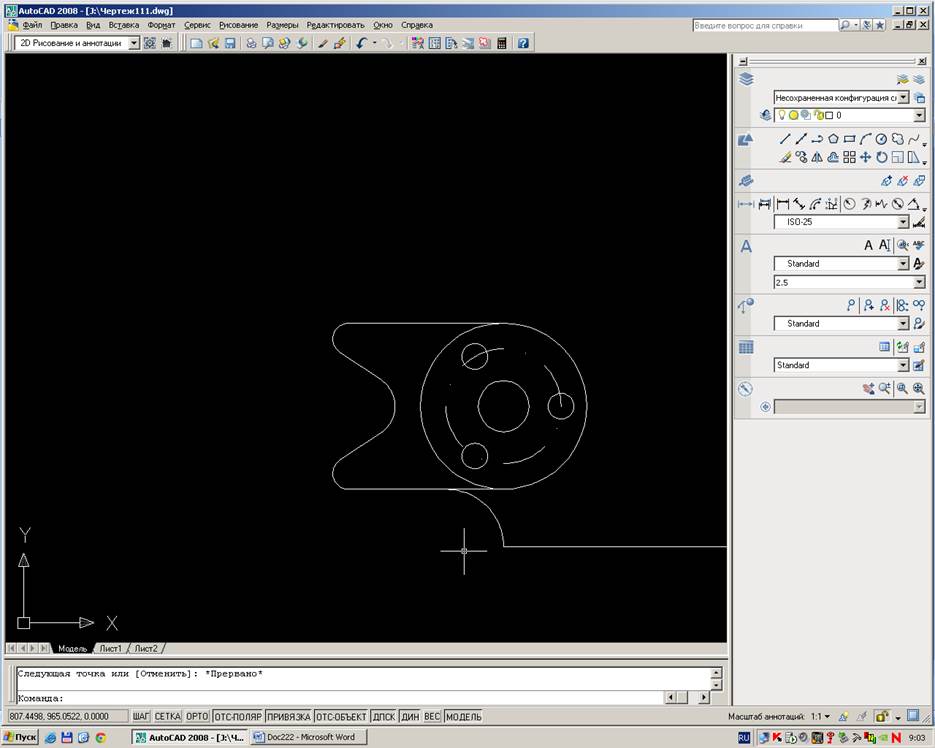
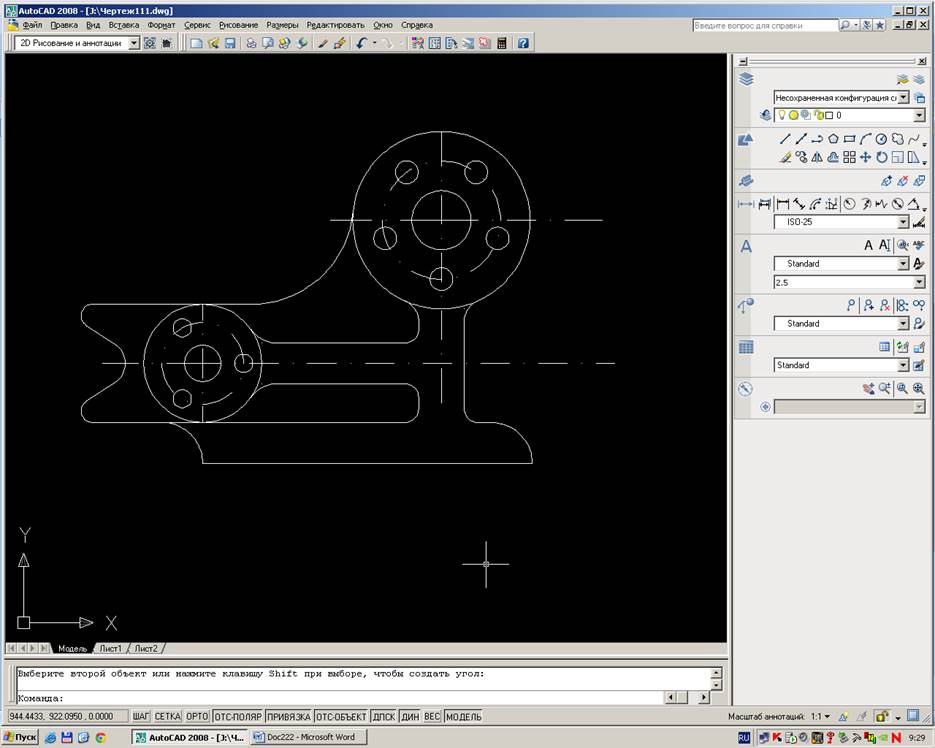
5. Сопрягаем правую и левую окружность радиусом R45 используя функцию Сопряжение.Проводим от левой окружности d52мм параллельные линии до пересеченияс вертикальными линиями от правой окружности d78мм.Затем проводим сопряжения с левой,правой окружностью и в точках пересечения опускных линий.
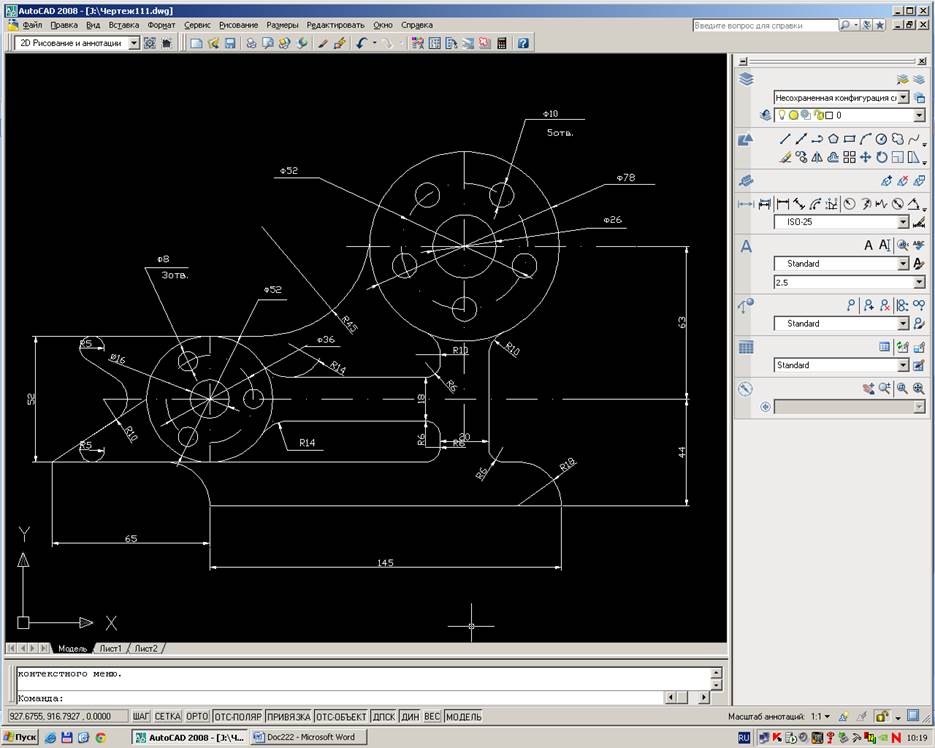
6.Наносим все размеры на полученный чертёж.
7. Наносим подпись с названием детали под чертежом.
Видео:Деление окружностей на равные частиСкачать
ЛАБОТАТОРНО — ПРАКТИЧЕСКАЯ РАБОТА №3 «ЧЕРТЕЖ ДЕТАЛИ С ПРИМЕНЕНИЕМ ДЕЛЕНИЯ ОКРУЖНОСТЕЙ НА РАВНЫЕ ЧАСТИ. ФЛАНЕЦ, ПРОКЛАДКА, РЕШЕТКА»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Лаботаторно — практическая работа №3
«Чертеж детали с применением деления окружностей на равные части. Фланец, прокладка, решетка»
Цель лабораторно — практической работы:
Целью настоящей работы является ознакомление студентов с правилами деления окружности на равное количество частей, а также приобретение ими навыков вычерчивания детали с применением деления окружности.
Задачи лабораторно- практической работы:
1. Изучить теоретический материал по теме
2. Выполнить упражнение на формате А4
строить параллельные и перпендикулярные линии;
правила определения центра дуги, деление отрезка прямой, деление углов;
правила построения вписанных многоугольников;
Количество часов: 2 часа
Перечень приборов, устройств, инструмента и других технических и материальных средств и оборудования, используемых для выполнения лабораторной работы:
Учебно-методическая литература: [1, с 29…25], ГОСТ 2.303-68, ГОСТ 2.307-2011
Чертежные принадлежности: чертежная бумага (формат А4), набор чертежных карандашей, мерительная линейка, угольники, лекала, транспортир, трафареты, шаблоны, циркуль чертежный.
План выполнения лабораторно — практической работы:
На выбранном формате бумаги (формат А4) выполнить рамку и внизу справа основную надпись.
Определить, сколько отверстий имеется в детали
Разделить окружность на нужное количество частей
С помощью угольника, рейсшины и циркуля выполнить необходимые построения.
Нанести размеры на чертеж детали.
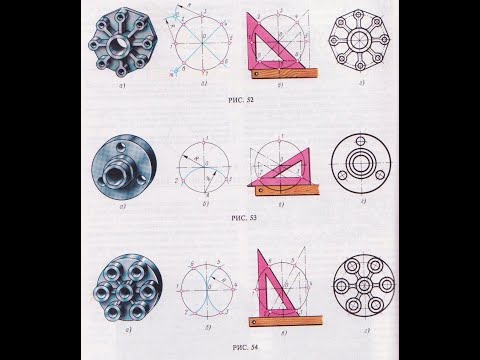
Некоторые детали машин и приборов имеют элементы, равномерно расположенные по окружности. При выполнении таких деталей необходимо знать правила деления окружности на равное количество частей.
1. Деление окружности на четыре равные части и построение правильного вписанного четырехугольника.
Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части в соответствии с рисунком 1. Соединив точки пересечения этих линий с окружностью прямыми, получим правильный вписанный четырехугольник.
Рисунок 1- Деление Рисунок 2 – Деление на
на четыре части восемь частей
2. Деление окружности на восемь равных частей и построение правильного вписанного восьмиугольника.
Две взаимно перпендикулярные линии, проведенные под углом 45 к центровым линиям с помощью угольника с углами 45, 45 и 90 и рейсшины в соответствии с рисунком 2. вместе с центровыми линиями разделять окружность на восемь равных частей.
Деление окружности на восемь равных частей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5 в соответствии с рисунком 3. Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.
Если полученные точки соединить последовательно прямыми линиями, то получится правильный восьмиугольник
Рисунок 3 — Деление окружности на восемь равных частей
3. Деление окружности на три равные части и построение правильного вписанного треугольника.
Данные построения выполняют с помощью циркуля или угольника с углами 30, 60 и 90 и рейсшины.
При делении окружности циркулем на три равные части из любой точки окружности, например из точки А пересечения центровых линий с окружностью, в соответствии с рисунком 4, проводят дугу радиусом R , равным радиусу данной окружности, получают точки 1 и 2. Третья точка деления (точка 3) будет находиться на противоположном конце диаметра, проходящего через точку А.
Рисунок 4 — Деление окружности циркулем на три равные части
Последовательно соединив точки 1, 2 и 3, получим правильный вписанный треугольник. При построении правильного вписанного треугольника, если задана одна из его вершин (например, точка 1), находят точку А. Для этого через заданную точку 1 проводят диаметр , рисунок 4 в). Точка А будет находиться на противоположном конце этого диаметра. Затем проводят дугу радиусом R , равным радиусу данной окружности, и получают точки 2 и 3.
5. Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника.
Данные построения выполняют с помощью циркуля или угольника с углами 30, 60 и 90 и рейсшины.
При делении окружности на шесть равных частей циркулем из двух концов одного диаметра радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в точках 2, 6 и 3, 5.
Последовательно соединив полученные точки, получим правильный вписанный шестиугольник в соответствии с рисунком 5
Рисунок 5 — Деление окружности на шесть равных частей
6. Деление окружности на двенадцать равных частей и построение правильного вписанного двенадцатиугольника.
Данные построения выполняют с помощью циркуля или угольника с углами 30, 60 и 90 и рейсшины.
При делении окружности циркулем из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью в соответствии с рисунком 6, а. Соединив полученные точки, получают правильный вписанный двенадцатиугольник в соответствии с рисунком 6,б.
Рисунок 6 — Деление окружности на двенадцать равных частей
7. Деление окружности на пять и десять равных частей и построение правильных вписанных пятиугольника и десятиугольника.
Половину любого диаметра (радиус) делят пополам, получают точку А в соответствии с рисунком 7,а. Из точки А, как из центра, проводят дугу радиусом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра, в точке В, в соответствии с рисунком 7,б. Отрезок 1В равен хорде, стягивающей дугу, длина которой равна 1/5 длины окружности.
Рисунок 7 — Деление окружности на пять и десять равных частей
Делая засечки на окружности, соответствии с рисунком 7, в, радиусом R , равным отрезку 1В, делят окружность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки 1 строят точки 2 и 5, затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1В, то построения выполнены правильно в соответствии с рисунком 7,г.
Деление окружности на десять равных частей выполняют аналогично делению окружности на пять равных частей, но сначала делят окружность на пять частей, начиная построение из точки 1, а затем из точки 6, находящейся на противоположном конце диаметра. В соответствии с рисунком 8,а. Соединив последовательно все точки, получают правильный вписанный десятиугольник в соответствии с рисунком 8,б.
Рисунок 8 — Деление окружности на пять и десять равных частей
9. Деление окружности на семь равных частей и построение правильного вписанного семиугольника.
Из любой точки, например точки А, радиусом заданной окружности проводят дугу до пересечения с окружностью в точках В и D в соответствии с рисунком 9,а. Соединим точки В и D прямой. Половина полученного отрезка ( в данном случае это отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1/7 длины окружности. Радиусом, равным отрезку ВС, делают засечки на окружности в последовательности, в соответствии с рисунком 9,б. Соединив последовательно все точки, получают правильный вписанный семиугольник, рисунок 9,в.
Рисунок 9 — Деление окружности на семь равных частей
10 . Деление окружности на любое число равных частей.
С достаточной точностью можно делить окружность на любое число равных частей, пользуясь таблицей коэффициентов для подсчета длины хорды (таблица 1):
Таблица 1- Коэффициенты для подсчета длины хорды
Видео:Видеоуроки по КОМПАС 3D. Урок 1 Деление окружности на равные частиСкачать

Практическая работа № 6 и 7 по теме : Деление окружности на равные части
Практическая работа №5 Нанесение размеров на чертежах деталей простой конфигурации
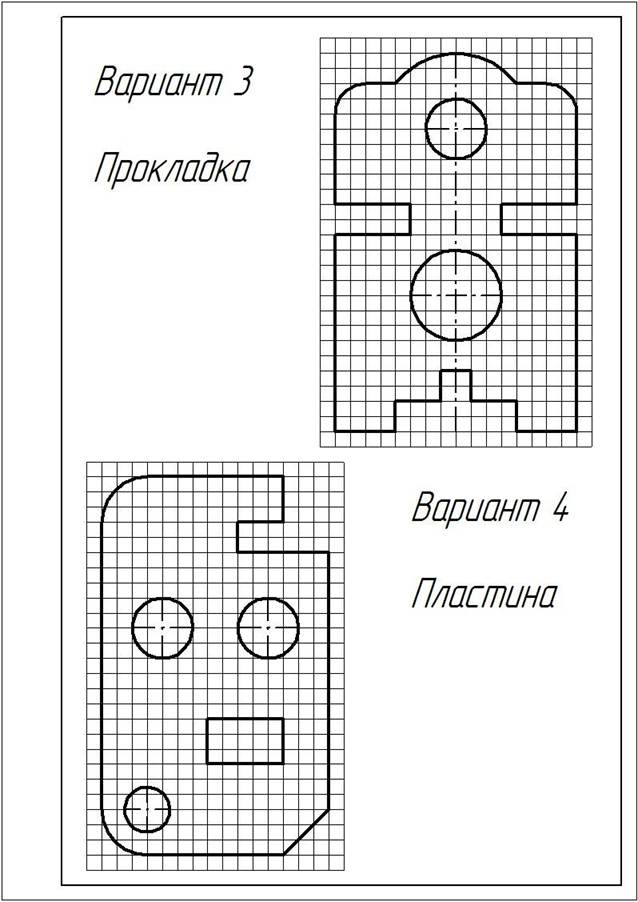
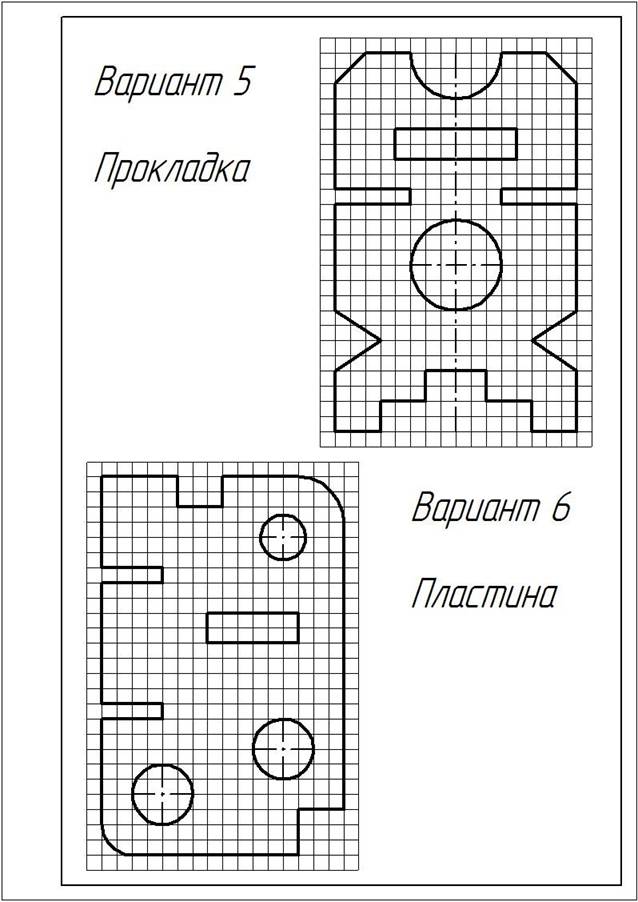
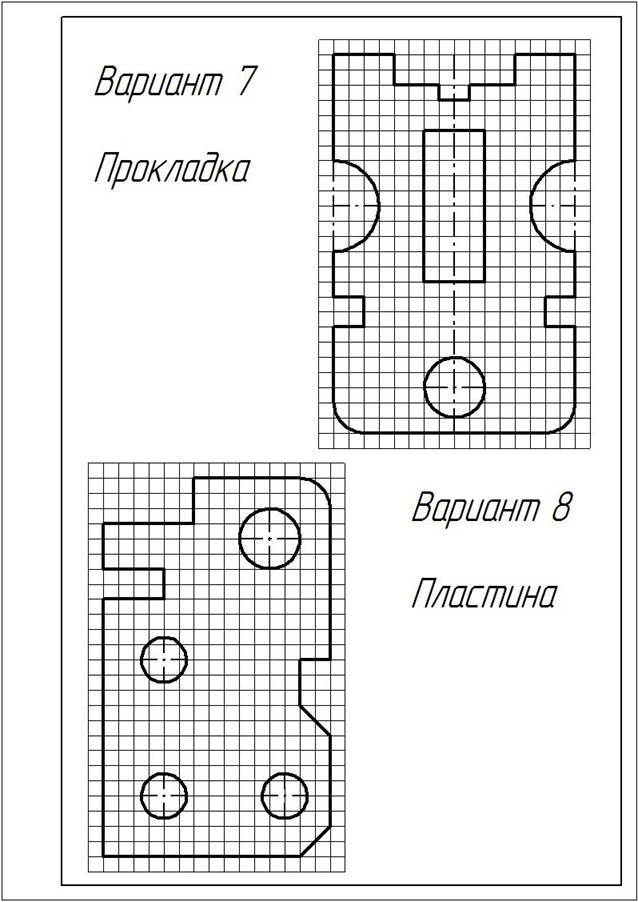
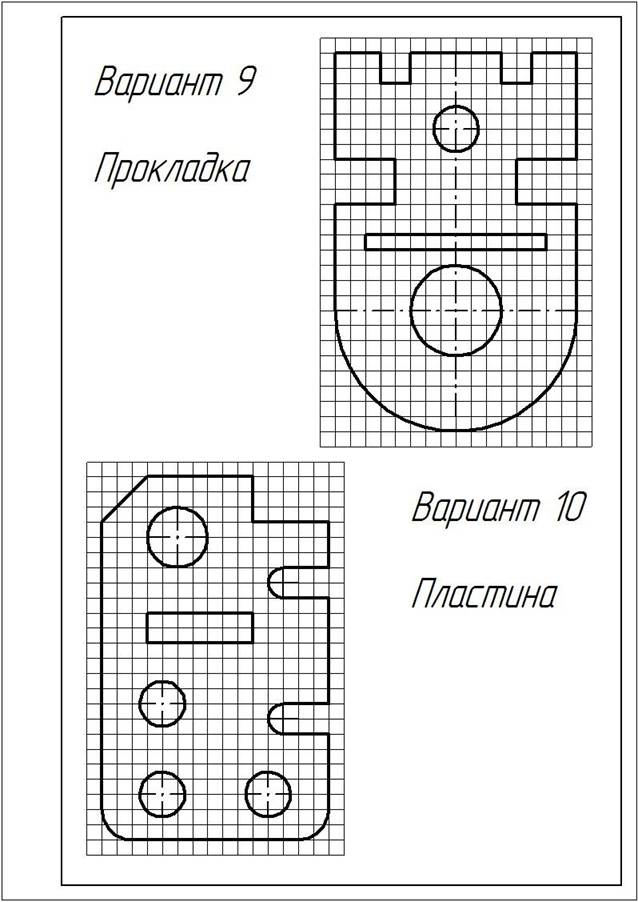
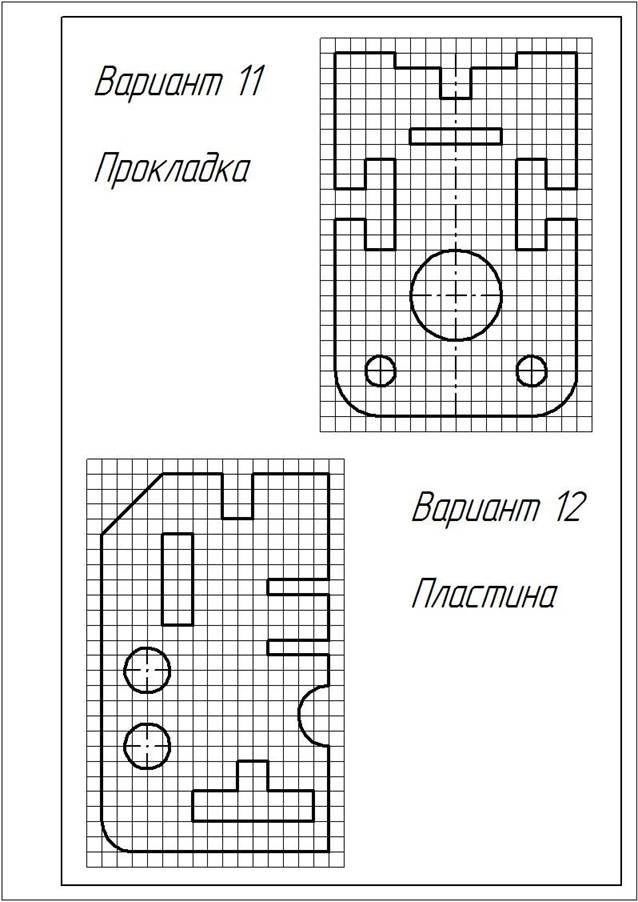
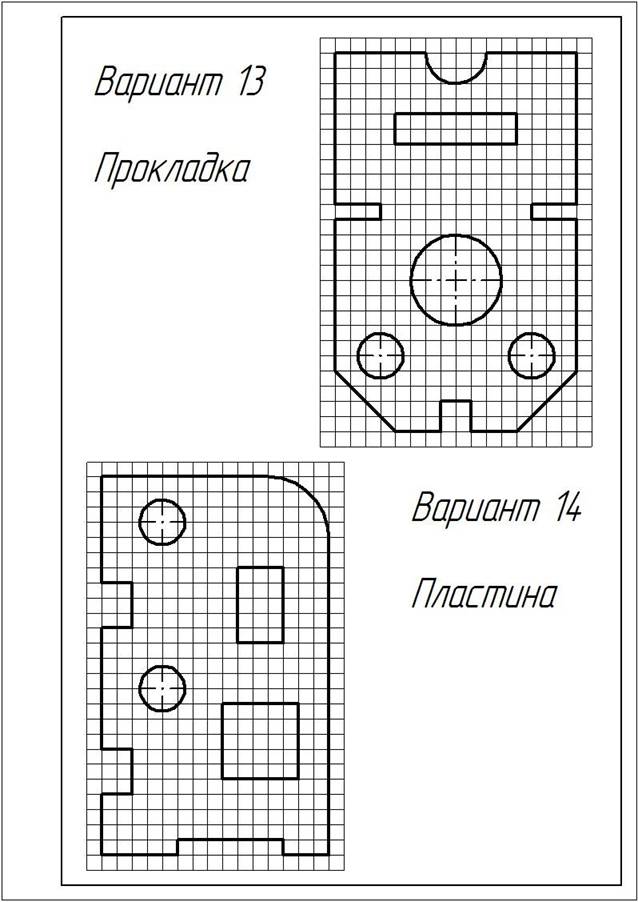
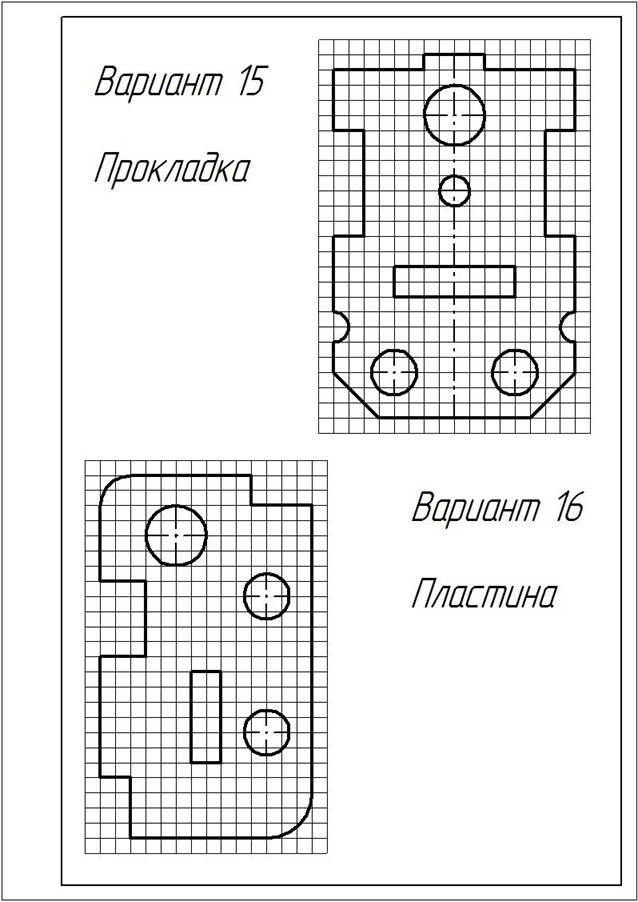
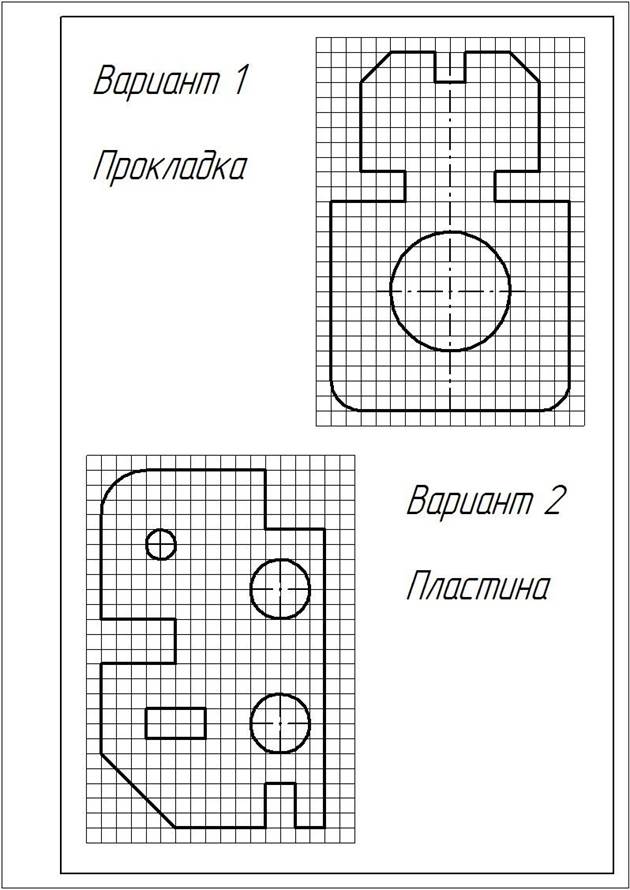
ЗАДАНИЕ:1. Перечертить деталь, определяя размеры по клеткам. Сторона клетки ровна 5 мм.
2. Поставить все необходимые размеры.
Методические указания к выполнению задания
1. Перед выполнением чертежа необходимо изучить задание (Приложение).
2. Работу над заданием начать с выполнения рамки чертежа(отступ от края формата: слева 20 мм, сверху, справа, снизу по 5 мм).
3. Далее выполнить планировку поля чертежа: изображение расположить на формате так, чтоб оно была одинаково удалена от всех сторон формата.
4. Поочередно выполнить первый и второй пункты задания.
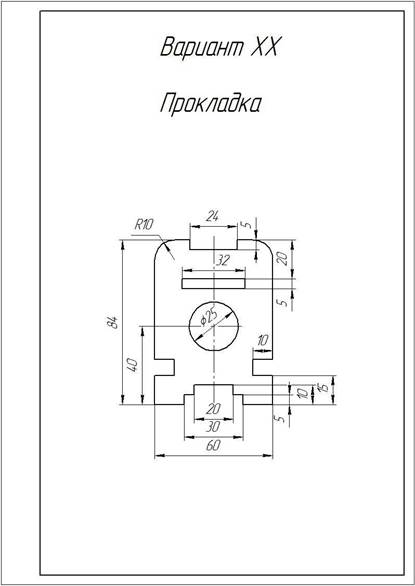 |
Образец выполнения задания
Варианты заданий
 |
Практическая работа № 6 и 7 по теме : Деление окружности на равные части
включает задание вычерчивания контуров деталей с применением рациональных методов деления окружности на равные части.
Необходимые чертежные инструменты и принадлежности (приобретаются студентом): ватман формата А3, карандаши, карандашный ластик, циркуль, линейка, угольники, транспортир, заточка для карандашей.
Раздаточный материал: плакат учебный, учебник «Инженерная графика» (1), Сборник заданий по инженерной графике (2).
Цель занятия: Научиться правильно выполнять деление окружности на части, сопряжения прямых, окружностей и по заданным размерам выполнять изображение детали и правильно проставлять их. Научиться вычерчивать линии чертежа.
Для выполнения графической работы по вычерчиванию контура технической детали необходимо проработать по учебнику следующие темы:
1 – линии чертежа
2 – простановка размеров на чертежах
3 — деление окружности на равные части и построение правильных вписанных многоугольников
Для правильного выполнения графической работы необходимо ознакомиться с ГОСТ 2.303-68 и 2. 304-81 ЕСКД.
1. ГОСТ 2.303-68 (Приложение 1) рекомендует выбирать толщину линий, длину штрихов и промежутки между ними в зависимости от формата чертежей и размера изображений. При проведении линий на чертеже нужно добиваться соблюдения отношения толщин различных по типу линий, выдерживать длину штрихов и промежутков между ними.
При этом следует учитывать рекомендации:
— центровые линии в центре окружности должны обязательно пересекаться своими штрихами, а не точками;
— штрихи должны выходить за пределы окружности на 3 — 4 мм;
— штрихпунктирная линия должна заканчиваться штрихом, а не точкой.
При начертании линий размеры их элементов следует брать из табл. 1.
2. При вычерчивании контура технической детали, вначале изучите ее контур, симметричность по вертикали или горизонтали, определите:
— габаритные размеры и место расположения изображения на поле чертежа;
— проведите оси симметрии изображения для основной окружности. Эти две линии являются базами для отсчёта, других размеров;
— построение остальных частей детали проводите согласно изображению на чертеже от базы отсчета;
— выполните деление окружности на необходимое количество частей, постройте заданный контур с использованием окружностей или их центров;
— по заданным радиусам сопряжений, определите центры и точки сопряжений, и проведите необходимые сопряжения.
3. — Проставляя размеры отдельных элементов детали, нужно решить следующие вопросы:
— какими размерами можно определить форму того или иного элемента;
— его местоположение по отношению к какой-то выбранной базе или другому элементу;
— как расставить размеры всех элементов на чертеже, как скомпоновать их.
Нужно стремиться к тому, чтобы размеры одного и того же элемента были сосредоточе — ны в одном месте (для удобства чтения) там, где этот элемент и его расположение наиболее наглядно и удобно читаются. Размерные числа должны иметь высоту 3,5 мм.
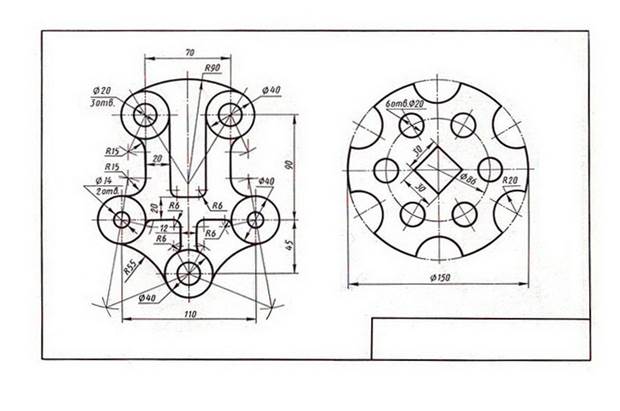
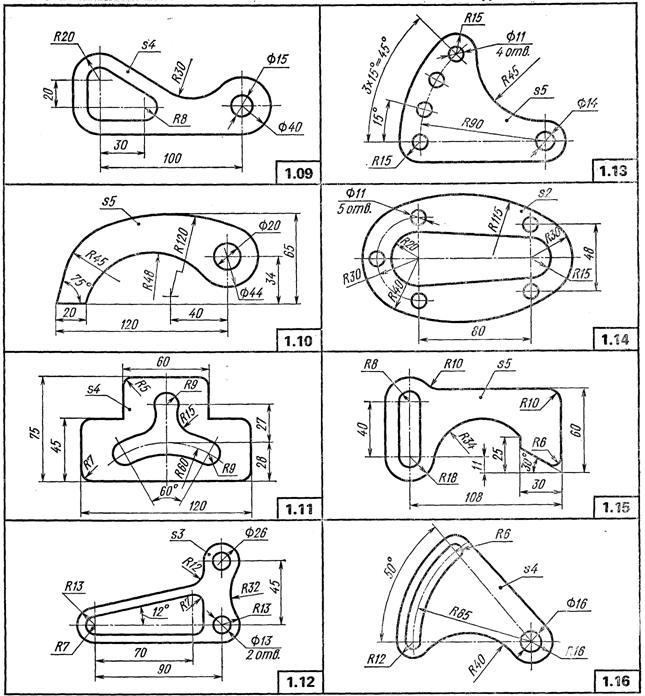
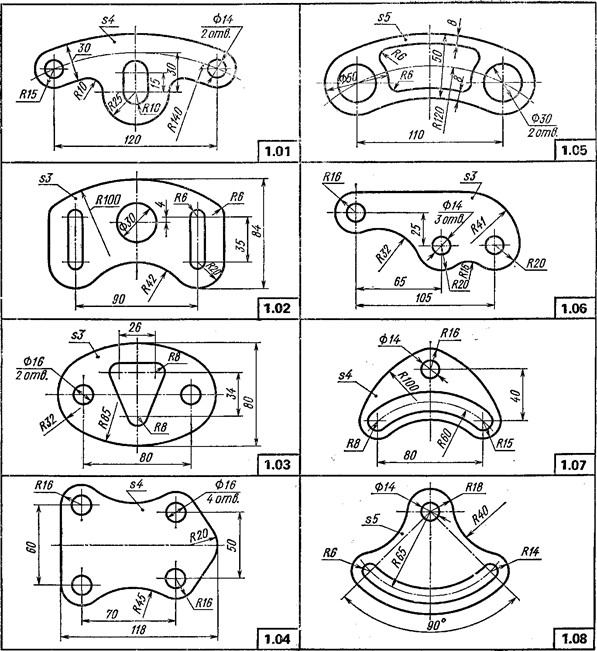
На листе формата А3 вычертить контур детали по своему варианту в масштабе 1:1, по заданным размерам, с применением правил построения сопряжений и деления окружности на части.
| Вариант 1, 11, 21 | 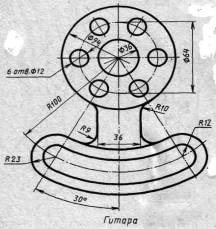 Гитара Гитара | Вариант 2, 12, 22 | 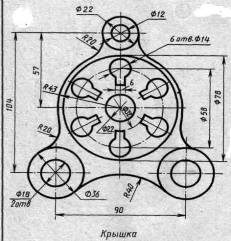 Крышка Крышка |
| Вариант 3, 13, 23 | 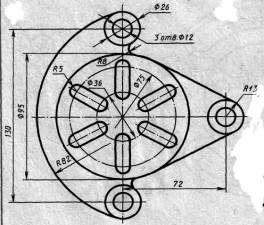 Подвеска Подвеска | Вариант 4, 14, 24 | 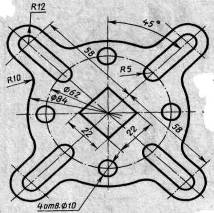 Подвеска Подвеска |
| Вариант 5, 15, 25 | 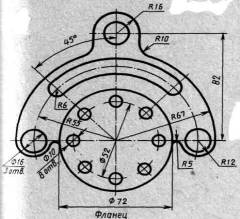 Фланец Фланец | Вариант 6, 16, 26 | 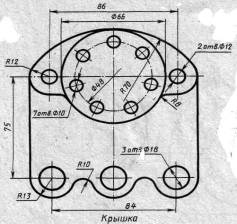 Крышка Крышка |
| Вариант 7, 17, 27 | 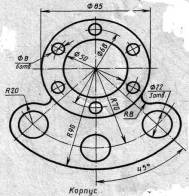 Корпус Корпус | Вариант 8, 18, 28 | 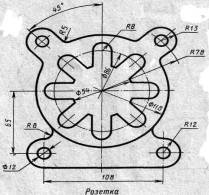 Розетка Розетка |
| Вариант 9, 19, 29 | 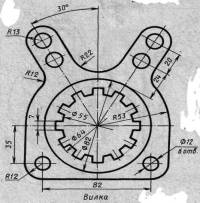 Вилка Вилка | Вариант 10, 20, 30 | 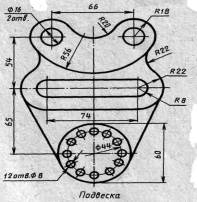 Подвеска Подвеска |
Порядок выполнения задания:
1 — определите габаритные размеры детали;
2 — выполните компоновку (определите ее положение на чертеже);
3 — для симметричной детали проведите ось симметрии;
4 — выполните контур детали, начиная с основной окружности;
5 — проставьте размеры в соответствии со стандартами ЕСКД;
5 — выполните обводку линий по ГОСТ 2.303-68
6 — завершая чертеж, проверьте правильность выполнения линий чертежа, стрелок, размерных чисел.
7 — заполните основную надпись. Код чертежа СПТ ИГ 01.02.00 (для 1 варианта).
При вычерчивании контуров технических деталей и других технических построениях часто приходится выполнять сопряжения (плавные переходы) от одних линий к другим и деление окружности на части. В приложении 3 приведены примеры деления окружности на части и построение сопряжений, когда задан радиус дуги сопряжения. В этом случае необходимо определить центр сопряжения и точки сопряжения. Обводку контура детали производят с помощью циркуля. При этом необходимо на чертеже сохранить линии построения центров и точек сопряжения.
— для симметричных элементов размер наносят один раз;
— габаритные размеры стоят последними, ближе всего к контуру детали — самый меньший из вынесенных размеров; применяйте упрощения типа: 2 отв.Ǿ10;
— на чертеже следует сохранить в тонких линиях вспомогательные построения сопряжения.
1 — как определяют точки на окружности при делении ее на 4,3 и 6 частей?
2 — как определяется центр сопряжений и точки сопряжения при сопряжении:
— прямой и окружности (внешнее и внутреннее сопряжение)?;
— двух окружностей (внешнее, внутреннее и смешанное сопряжение)?;
— каким знаком обозначается уклон, каким конусность, и как определяется и обозначается уклон и конусность?
3 — объясните по своему чертежу деление окружности на части, построение сопряжений: нахождение центра сопряжений и точки сопряжений
Графическая работа № 7
Графическая работа включает два задания: вычерчивание сопряжений и нанесение размеров на чертежах в соответствии с ГОСТ 2.307-68.
Необходимые чертежные инструменты и принадлежности (приобретаются студентом): ватман формата А3, карандаши, карандашный ластик, циркуль, линейка, угольники, транспортир, заточка для карандашей.
Раздаточный материал: плакат учебный, учебник «Инженерная графика» (1), Сборник заданий по инженерной графике (2).
Время выполнения Графической работы № 3 – 4 учебных часа.
Пример задания для выполнения Графической работы № 3 приведен на рисунке ниже.
Название работы:Построение сопряжений двух прямых дугой окружности заданного радиуса, дуг с дугами и дуги с прямой.
— изучение методов построения сопряжений, приобретение навыков в выполнении геометрических построений, продолжение закрепления навыков работы с чертежными инструментами и оформления чертежа;
— способствование развитию пространственного воображения, логического мышления. Основные понятия: (при необходимости)
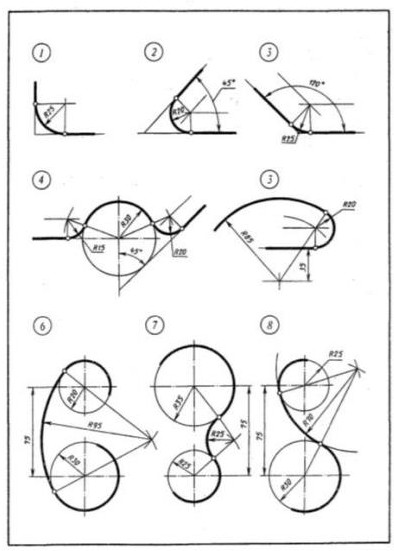
Исходные данные (задание): Выполнить примеры построения сопряжений и нанести размеры. Задание выполняется в одном варианте. Масштаб 1:1.
 |
Порядок выполнения: Методические указания по выполнению работы.
При выполнении чертежа рекомендуется соблюдать следующую последовательность: 1. Подготовить формат листа А-4, начертить внешнюю и внутреннюю рамки чертежа, отвести место для основной надписи и дополнительной графы. Масштаб изображения М 1:1 2. Провести осевые и центровые линии, взяв расстояние между ними согласно размерам детали и учитывая равномерность распределения изображений на поле чертежа. 3. Провести дуги окружностей, окружности и прямые линии, положение которых определено заданными размерами и не требует дополнительных построений. 4. Выполнить геометрические построения и сопряжения. Предварительные построения выполнять тонкими линиями твердым карандашом (Т или 2Т). 5. Нанести выносные и размерные линии, надписать размерные числа (шрифт 5). 6. Проверить правильность выполнения чертежа и обвести
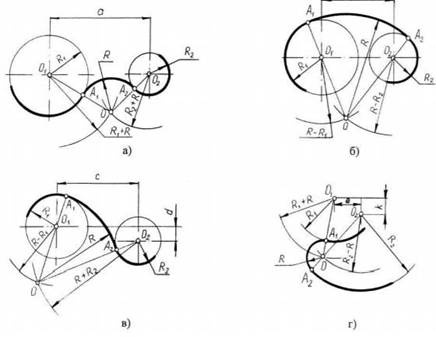
чертеж карандашом (ТМ или М). Вначале обвести дугу окружностей и окружности, затем – прямые линии. Обвести внутреннюю рамку чертежа. Все построения сопряжений сохранить. Краткие сведения из теории. При выполнении чертежей деталей встречаются случаи плавного перехода от одной линии к другой, называемые сопряжениями. Различают виды сопряжений: a) Сопряжение двух прямых дугой окружности заданного радиуса; b) Сопряжение дуги окружности и прямой линии дугой заданного радиуса c) Сопряжение углов дугой заданного радиуса; Сопряжение двух окружностей дугой заданного радиуса. Различают внешнее, внутреннее и смешанное касания. Если одна окружность с центром О касается окружности с центром О1 с внешней стороны, то такое сопряжение называется внешним. При этом точка сопряжения В лежит на линии центров О и О1, а расстояние между центрами О и О1 равно сумме радиусов R + r (рис. 1а). Если одна окружность касается другой окружности внутри, то такое сопряжение называется внутренним, при этом точка сопряжения В лежит на линии центров ОО1 = R – r (рис. 1в).
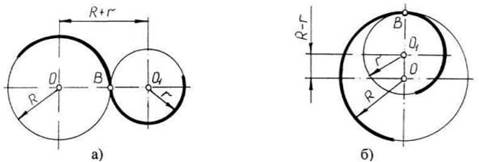 |
Рис.1 Внешнее и внутреннее сопряжения
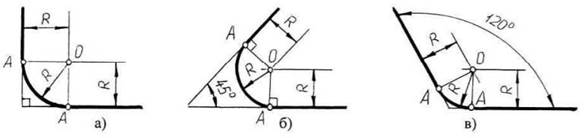
Чтобы построить сопряжение необходимо найти: 1. Центр сопряжения 2. Точки сопряжения Прежде чем начертить, необходимо провести анализ графического состава изображения, чтобы установить, какие геометрические построения необходимо применить. Сопряжение двух прямых линий (скругление углов) Здесь возможны три случая: прямые пересекаются под прямым углом друг к другу (рис.2,а), прямые пересекаются под острым углом и прямые пересекаются под тупым углом (рис.2,б,в,). Во всех трех случаях методика решения одна и та же. Параллельно сторонам угла, образованного данными прямыми, провести прямые на расстоянии заданного радиуса R. Точка пересечения этих прямых является центром О сопряжения. Из центра опустить перпендикуляры к сторонам данного угла и определить точки сопряжения А. Между точками А из центра О провести сопрягающую дугу радиуса R.
Рис.2 Построение сопряжения двух прямых линий
Сопряжение дуги окружности и прямой линии второй дугой Если прямая не пересекает окружность, то можно осуществить внешнее сопряжение (рис.3, а) и внутреннее сопряжение (рис.3, б). В первом случае необходимо провести вспомогательную прямую, параллельную заданной прямой, на расстоянии заданного радиуса R1 и из точки О вспомогательную окружность радиуса (R + R1). Пересечение вспомогательных линий даст центр дуги сопряжения О1. Опуская из точки О1 перпендикуляр на заданную прямую, найти точку сопряжения А, а соединяя точку О1 с О, найти точку сопряжения на заданной окружности А1. Во втором случае построение аналогично предыдущему случаю, но так как сопряжение внутреннее, то вспомогательную окружность проводят радиусом R1 R (рис.13, б). Построение сопряжения прямой с окружностью радиуса R, когда прямая пересекает окружность (рис.3, в), аналогично предыдущему, то есть необходимо провести вспомогательную прямую параллельно заданной прямой на расстоянии радиуса R1 и вспомогательную окружность радиусом R — R1. Затем найти точки сопряжения А и А1.
Сопряжение двух дуг окружностей третьей дугой В данном случае сопрягающая дуга радиуса R может касаться заданных дуг радиусов R1 и R2 с внешней стороны (рис.4, а), создавать внутреннее касание (рис.4, б) или сочетание внешнего и внутреннего касания (рис.4, в, г). При построении внешнего сопряжения центр О искомой дуги радиуса R находится на пересечении вспомогательных окружностей, проведенных из центров О1 и О2 соответствующими радиусами R + R1 и R + R2. Соединяя О1 и О2 с О, необходимо найти точки сопряжения А1 и А2. Между точками А1 и А2 из центра О провести сопрягающую дугу радиуса R (рис.4, а).
Рис.4. Построение сопряжения двух дуг окружностей третьей дугой.
Построение внутреннего касания аналогично, только вспомогательные окружности проводят радиусами R — R1 и R — R2 (рис.4, б). При построении смешанного касания (сочетание внутреннего и внешнего) центр сопряжения находится на пересечении вспомогательных окружностей радиусами R- R1 и R + R2 (рис.4, в, г). Затем необходимо найти точки сопряжения А1, А2 и соединить их сопрягающей дугой. Нанесение размеров Величины изображенного изделия и его элементов на чертежах определяются размерами, общее число которых должно быть минимальным, но достаточным для его изготовления и контроля. Линейные размеры указывают в миллиметрах без обозначения единиц. Угловые единицы указывают на чертеже в градусах (°). Правила нанесения размеров установлены ГОСТ 2.307- 68*. Размеры на чертежах указывают размерными линиями. Размерные линии ограничивают стрелками (рис.16, а), которые острием касаются выносных линий, линий контура, осевых линий. Выносная линия выступает за стрелку на 12 мм. Размерную линию проводят параллельно отрезку, размер которого указывают, по возможности, вне контура изображения (рис.16, б). Расстояние от размерной линии до контура и между параллельными размерными линиями должно быть 10 мм. Размерные линии не должны быть продолжением линий контура, осевых, центровых и выносных линий. Все перечисленные линии не могут быть использованы в качестве размерных. Размерные линии не должны 17 пересекаться с выносными, поэтому меньшие размеры наносят ближе к линиям контура, а большие дальше. Форму стрелки и ее размеры выдерживают на чертеже одинаковыми. Каждый размер указывается только один раз. Размерные числа наносят над размерной линией возможно ближе к ее середине. Для обозначения диаметра перед размерным числом наносят знак Ф, для обозначения радиуса R (рис.16, в), размеров квадратных элементов — □. Размерную линию при указании величины углов проводят в виде дуги с центром в вершине угла. Перечень оборудования: (ТСО, наглядные пособия): Плакаты.
Задание
1. Что такое сопряжение?
2. Как определить точку касания при построении окружности, касательной к прямой?
3. На чем основан общий прием нахождения центра сопрягающей дуги?
4. Как выполняется сопряжение двух заданных окружностей дугой заданного радиуса?
5. Как выполняется сопряжение двух пересекающихся прямых?
🎦 Видео
Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

1 2 4 сопряжение окружностейСкачать

Деление окружности на n- равные частиСкачать

ВСЯ СУТЬ СОПРЯЖЕНИЙ И ПЕРЕХОДОВ. Правило построения сопряжений. Геометрические построенияСкачать

Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Деление окружности на 3; 6; 12 равных частейСкачать

Деление окружности на 3 частиСкачать

Деление окружности на N равных частей. Урок 8. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Деление окружности на равные части с помощью циркуляСкачать

Деление окружности на 12 равных частейСкачать

НАЧЕРТИТЬ ЗАСОВ. ГЕОМЕТРИЧЕСКОЕ ЧЕРЧЕНИЕ. ИНЖЕНЕРНАЯ ГРАФИКА. ПЕРЕХОДЫ И СОПРЯЖЕНИЯСкачать

деление окружности на произвольное число частейСкачать
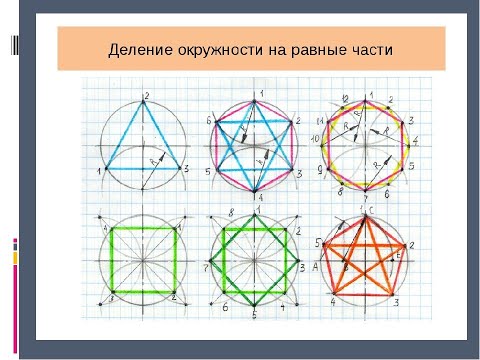
Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать

1 2 2 деление окружности на 5 равных частейСкачать

Деление отрезка на равные части, перпендикуляр к прямой.Урок 4.(Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Деление окружностейСкачать

Деление окружности на равные части. Внимание!!! В таблице имеются ошибки. ПОЛЬЗУЙТЕСЬ ФОРМУЛОЙ!!!Скачать