Вся теория по теме окружность 8 9 класс атанасян

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Определение окружности

• Отрезки в окружности

Определение окружности

Окружность – геометрическое место точек, равноудаленных от данной точки.

Эта точка называется центром окружности .

Отрезки в окружности

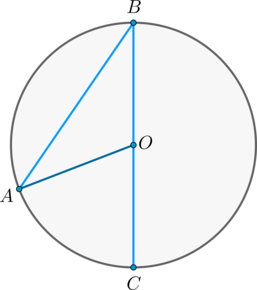
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.

Дуга в окружности

Часть окружности, заключенная между двумя точками, называется дугой окружности .

Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .

Теорема 4:
Равные хорды стягивают равные дуги.

Если A B = C D , то ∪ A B = ∪ C D

Углы в окружности

В окружности существует два типа углов: центральные и вписанные.

Центральный угол – угол, вершина которого лежит в центре окружности.

∠ A O B – центральный.

Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α

Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.

Градусная мара всей окружности равна 360 ° .

Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ A C B – вписанный.

Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α

Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2

Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .

∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °

Длина окружности, длина дуги

Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .

Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .

Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.

Длина окружности находится по формуле:

Длина дуги окружности , на которую опирается центральный угол α равна:

l α = π R 180 ∘ ⋅ α

Площадь круга и его частей

Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.

Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.

Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.

Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.

Площадь круга находится по формуле: S = π R 2

Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.

Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α

Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.

Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.

S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α

Теорема синусов

Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с окружностями.

Окружность. Основные теоремы

Определения

Центральный угол – это угол, вершина которого лежит в центре окружности.

Вписанный угол – это угол, вершина которого лежит на окружности.

Градусная мера дуги окружности – это градусная мера центрального угла, который на неё опирается.

Теорема

Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.

Доказательство

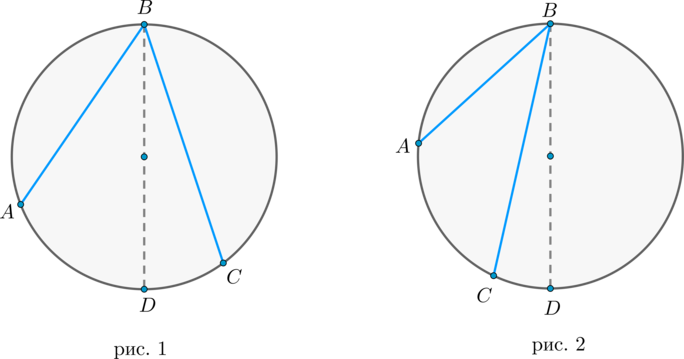
Доказательство проведём в два этапа: сначала докажем справедливость утверждения для случая, когда одна из сторон вписанного угла содержит диаметр. Пусть точка (B) – вершина вписанного угла (ABC) и (BC) – диаметр окружности:

Треугольник (AOB) – равнобедренный, (AO = OB) , (angle AOC) – внешний, тогда (angle AOC = angle OAB + angle ABO = 2angle ABC) , откуда (angle ABC = 0,5cdotangle AOC = 0,5cdotbuildrelsmileover) .

Теперь рассмотрим произвольный вписанный угол (ABC) . Проведём диаметр окружности (BD) из вершины вписанного угла. Возможны два случая:

1) диаметр разрезал угол на два угла (angle ABD, angle CBD) (для каждого из которых теорема верна по доказанному выше, следовательно верна и для исходного угла, который является суммой этих двух и значит равен полусумме дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 1.

2) диаметр не разрезал угол на два угла, тогда у нас появляется ещё два новых вписанных угла (angle ABD, angle CBD) , у которых сторона содержит диаметр, следовательно, для них теорема верна, тогда верна и для исходного угла (который равен разности этих двух углов, значит, равен полуразности дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 2.

Следствия

1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.

2. Вписанный угол, опирающийся на полуокружность, прямой.

3. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.

Определения

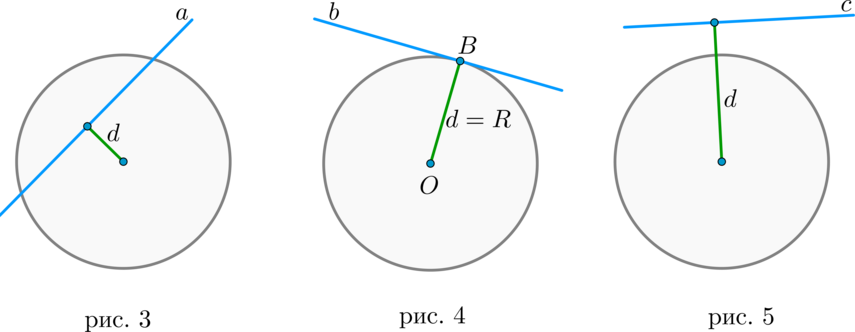
Существует три типа взаимного расположения прямой и окружности:

1) прямая (a) пересекает окружность в двух точках. Такая прямая называется секущей. В этом случае расстояние (d) от центра окружности до прямой меньше радиуса (R) окружности (рис. 3).

2) прямая (b) пересекает окружность в одной точке. Такая прямая называется касательной, а их общая точка (B) – точкой касания. В этом случае (d=R) (рис. 4).

3) прямая (c) не имеет общих точек с окружностью (рис. 5).

Теорема

1. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.

2. Если прямая проходит через конец радиуса окружности и перпендикулярна этому радиусу, то она является касательной к окружности.

Следствие

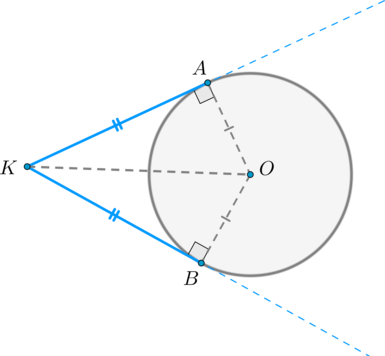
Отрезки касательных, проведенных из одной точки к окружности, равны.

Доказательство

Проведем к окружности из точки (K) две касательные (KA) и (KB) :

Значит, (OAperp KA, OBperp KB) как радиусы. Прямоугольные треугольники (triangle KAO) и (triangle KBO) равны по катету и гипотенузе, следовательно, (KA=KB) .

Следствие

Центр окружности (O) лежит на биссектрисе угла (AKB) , образованного двумя касательными, проведенными из одной точки (K) .

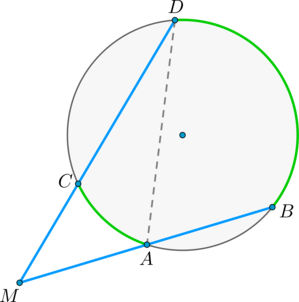
Теорема об угле между секущими

Угол между двумя секущими, проведенными из одной точки, равен полуразности градусных мер большей и меньшей высекаемых ими дуг.

Доказательство

Пусть (M) – точка, из которой проведены две секущие как показано на рисунке:

Покажем, что (angle DMB = dfrac(buildrelsmileover — buildrelsmileover)) .

(angle DAB) – внешний угол треугольника (MAD) , тогда (angle DAB = angle DMB + angle MDA) , откуда (angle DMB = angle DAB — angle MDA) , но углы (angle DAB) и (angle MDA) – вписанные, тогда (angle DMB = angle DAB — angle MDA = fracbuildrelsmileover — fracbuildrelsmileover = frac(buildrelsmileover — buildrelsmileover)) , что и требовалось доказать.

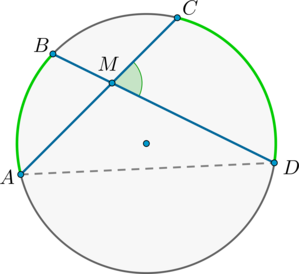
Теорема об угле между пересекающимися хордами

Угол между двумя пересекающимися хордами равен полусумме градусных мер высекаемых ими дуг: [angle CMD=dfrac12left(buildrelsmileover+buildrelsmileoverright)]

Доказательство

(angle BMA = angle CMD) как вертикальные.

Из треугольника (AMD) : (angle AMD = 180^circ — angle BDA — angle CAD = 180^circ — frac12buildrelsmileover — frac12buildrelsmileover) .

Но (angle AMD = 180^circ — angle CMD) , откуда заключаем, что [angle CMD = frac12cdotbuildrelsmileover + frac12cdotbuildrelsmileover = frac12(buildrelsmileover + buildrelsmileover).]

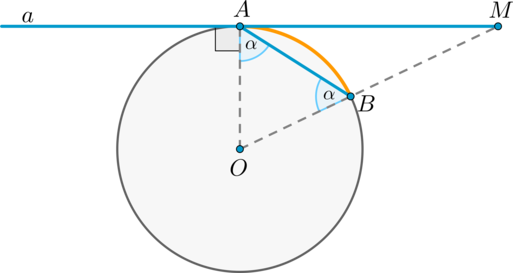
Теорема об угле между хордой и касательной

Угол между касательной и хордой, проходящей через точку касания, равен половине градусной меры дуги, стягиваемой хордой.

Доказательство

Пусть прямая (a) касается окружности в точке (A) , (AB) – хорда этой окружности, (O) – её центр. Пусть прямая, содержащая (OB) , пересекает (a) в точке (M) . Докажем, что (angle BAM = frac12cdot buildrelsmileover) .

Обозначим (angle OAB = alpha) . Так как (OA) и (OB) – радиусы, то (OA = OB) и (angle OBA = angle OAB = alpha) . Таким образом, (buildrelsmileover = angle AOB = 180^circ — 2alpha = 2(90^circ — alpha)) .

Так как (OA) – радиус, проведённый в точку касания, то (OAperp a) , то есть (angle OAM = 90^circ) , следовательно, (angle BAM = 90^circ — angle OAB = 90^circ — alpha = frac12cdotbuildrelsmileover) .

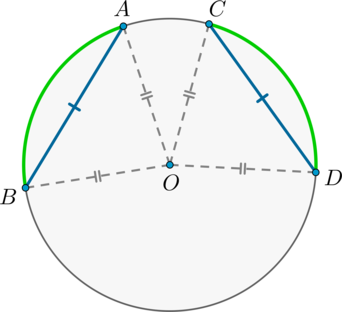
Теорема о дугах, стягиваемых равными хордами

Равные хорды стягивают равные дуги, меньшие полуокружности.

И наоборот: равные дуги стягиваются равными хордами.

Доказательство

1) Пусть (AB=CD) . Докажем, что меньшие полуокружности дуги (buildrelsmileover=buildrelsmileover) .

(triangle AOB=triangle COD) по трем сторонам, следовательно, (angle AOB=angle COD) . Но т.к. (angle AOB, angle COD) — центральные углы, опирающиеся на дуги (buildrelsmileover, buildrelsmileover) соответственно, то (buildrelsmileover=buildrelsmileover) .

2) Если (buildrelsmileover=buildrelsmileover) , то (triangle AOB=triangle COD) по двум сторонам (AO=BO=CO=DO) и углу между ними (angle AOB=angle COD) . Следовательно, и (AB=CD) .

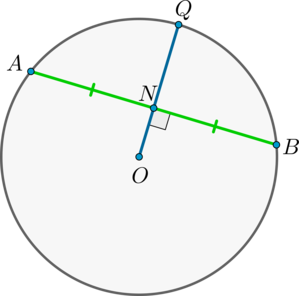
Теорема

Если радиус делит хорду пополам, то он ей перпендикулярен.

Верно и обратное: если радиус перпендикулярен хорде, то точкой пересечения он делит ее пополам.

Доказательство

1) Пусть (AN=NB) . Докажем, что (OQperp AB) .

Рассмотрим (triangle AOB) : он равнобедренный, т.к. (OA=OB) – радиусы окружности. Т.к. (ON) – медиана, проведенная к основанию, то она также является и высотой, следовательно, (ONperp AB) .

2) Пусть (OQperp AB) . Докажем, что (AN=NB) .

Аналогично (triangle AOB) – равнобедренный, (ON) – высота, следовательно, (ON) – медиана. Следовательно, (AN=NB) .

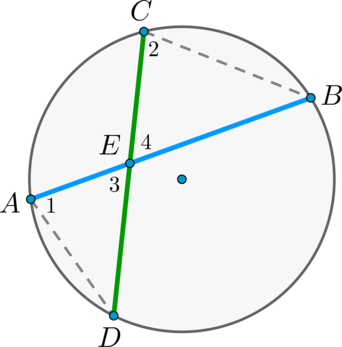
Теорема о произведении отрезков хорд

Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

Доказательство

Пусть хорды (AB) и (CD) пересекаются в точке (E) .

Рассмотрим треугольники (ADE) и (CBE) . В этих треугольниках углы (1) и (2) равны, так как они вписанные и опираются на одну и ту же дугу (BD) , а углы (3) и (4) равны как вертикальные. Треугольники (ADE) и (CBE) подобны (по первому признаку подобия треугольников).

Тогда (dfrac = dfrac) , откуда (AEcdot BE = CEcdot DE) .

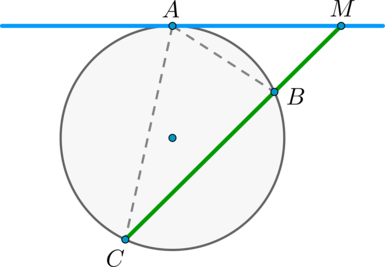
Теорема о касательной и секущей

Квадрат отрезка касательной равен произведению секущей на ее внешнюю часть.

Доказательство

Пусть касательная проходит через точку (M) и касается окружности в точке (A) . Пусть секущая проходит через точку (M) и пересекает окружность в точках (B) и (C) так что (MB . Покажем, что (MBcdot MC = MA^2) .

Рассмотрим треугольники (MBA) и (MCA) : (angle M) – общий, (angle BCA = 0,5cdotbuildrelsmileover) . По теореме об угле между касательной и секущей, (angle BAM = 0,5cdotbuildrelsmileover = angle BCA) . Таким образом, треугольники (MBA) и (MCA) подобны по двум углам.

Из подобия треугольников (MBA) и (MCA) имеем: (dfrac = dfrac) , что равносильно (MBcdot MC = MA^2) .

Следствие

Произведение секущей, проведённой из точки (O) , на её внешнюю часть не зависит от выбора секущей, проведённой из точки (O) :

Разработка уроков по геометрии 8 класс тема: «Окружность». Атанасян. Позиционный метод

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

МБОУ Мугудайская средняя общеобразовательная школа имени Д. Д. Красильникова

Разработка уроков с применением заданий по позиционным ролям по теме «Окружность» для учащихся 8 класса

Монастырева С. Л.

Тема урока: «Свойство биссектрисы треугольника и серединного перпендикуляра ».

Тип урока: Изучение нового материала, с применением заданий по позиционным ролям.

Обучающие: углубленное изучение теоретического материала по теме «Свойство биссектрисы треугольника и серединного перпендикуляра»;

Развивающие: Развитие мышления, логики, речи, воображения, умения анализировать и оценивать работу, развитие умения групповой работы;

Воспитательные: Воспитание чувства ответственности за качество и результат выполняемой работы.

Бланк ответов, карточки с заданиями для каждой группы, бумаги, в виде треугольника.

Приветствие учителя и подготовка к уроку .

Инструкция изучения нового материала

Для выполнения данной работы вы должны выполнить задания по позиционным ролям как: «Понятие», «Схема», «Историки».

Инструктаж: Каждая группа получает карточки с заданиями. Для выполнения одной задании дается 5 мин. После выполнения вы всей группой начинается защищать свою позицию.

Учащиеся делятся на группу, сидящих рядом по парте. (4-5 человек)

Учитель раздает каждой группе задания.

Ученики решают задачи.

Защита позиции «Понятие»

Задание: Найдите из разных источников понятие теоремы о биссектрисе треугольника, серединном перпендикуляре треугольника, какими свойствами они обладают.

«Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. Обратно: каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе. Биссектрисы треугольника пересекаются в одной точке. Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярна к нему. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка».

Защита позиции «Историк»

Найдите из разных источников, как называется точка пересечения биссектрисы и серединного перпендикуляра треугольника, какие ученые работали? Заполните таблицу. (Название точки, ученого, что пересекается)

Ученики должны проанализировать и найти правильный ответ

Защита позиции «Схема»

Покажите схематично доказательство теорему о серединном перпендикуляре, теорему о биссектрису угла, используя учебник или другой источник.

Дети показывают доказательство схематично, творчески выполняя свою позицию.

Итак, дети вам понравилось работать в группах?

Хотели бы работать в таких условиях?

Что нового вы узнали?

Тема урока: « Теорема о пересечения высот треугольника»

Тип урока: изучение нового материала, с применением заданий по позиционным ролям

Обучающие: углубленное изучение теоретического материала по теме « Теорема о пересечения высот треугольника »;

Развивающие: Развитие мышления, логики, речи, воображения, умения анализировать и оценивать работу, развитие умения групповой работы;

Воспитательные: Воспитание чувства ответственности за качество и результат выполняемой работы.

Оборудование: карточки с заданиями.

Приветствие учителя и подготовка к уроку .

Инструкция изучения нового материала

Для выполнения данной работы вы должны выполнить задания по позиционным ролям как: «Понятие», «Схема», «Историки».

Инструктаж: Каждая группа получает карточки с заданиями. Для выполнения одной задании дается 5 мин. После выполнения вы всей группой начинается защищать свою позицию.

Учащиеся делятся на группу, сидящих рядом по парте. (4-5 человек). Историки:

Учитель раздает каждой группе задания.

Ученики решают задачи.

Защита позиции «Понятие» (5мин)

Задание: Найдите из разных источников понятие теоремы о точке пересечения высот, о точке пересечения медиан треугольника, какими свойствами они обладают.

Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону или на её продолжение. Любой треугольник имеет три высоты. Высоты треугольника (или их продолжения) пересекаются в одной точке. Медианой треугольника называется отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Любой треугольник имеет три медианы. Медианы треугольника пресекаются в одной точке.

Защита позиции «Историки»

Найдите из разных источников, как называется точка пересечения высот и медиан треугольника, какие ученые работали? Заполните таблицу. (Название точки, ученого, что пересекается)

Ученики должны проанализировать и найти правильный ответ

Защита позиции «Схема»

Покажите схематично доказательство теорему о точке пересечения высот, теорему о пересечения медиан, используя учебник или другой источник.

Дети показывают доказательство схематично, творчески выполняя свою позицию.

Итак, дети вам понравилось работать в группах?

Что нового вы узнали?

Тема урока: « Четыре замечательные точки треугольника»

Тип урока: дифференцированный контроль знаний, с применением заданий по позиционным ролям

Образовательные: добиться результата дифференцированного контроля знаний о четырех замечательных точках треугольника.

Развивающие: формировать умение решать задачи с разными уровнями сложности.

Воспитательные: умение работать в тишине, не мешая другу по парте, умение не отвлекаться.

оценить свои умения решать задачи

овладеть умением решать задачи

Оборудование: карточки с заданиями

Сегодня, перед выполнением контрольной работы, вы должны выбрать вариант контрольной работы.

Учащиеся должны выбрать уровень знания.

1 вариант (30мин)

1. Отрезок BD является биссектрисой треугольника ABC. Найдите АВ, если ВС = 9 см, AD= 7,5 см, DC=4,5cm.

2. Серединный перпендикуляр к стороне ВС треугольника ABC пересекает сторону АС в точке D. Найдите: AD и CD, если BD=5 см, АС=8,5 см.

3. Медиана AD треугольника ABC продолжена за сторону ВС на отрезок DE, равный AD, и точка Е соединена с точкой С. найдите ∠ ACE, если ∠ ACD = 56°, ∠ ABD = 40°.

4. Треугольник АВС, АК и ВД- высоты треугольника, пересекающиеся в точке О, ∠ САВ=42°. Найти ∠ АСО.

1.

2.

3.

4. Приведем еще одну высоту СМ, по теореме пересечении высот треугольника СМ пройдет через точку О, а значит, треугольник АСМ- прямоугольный. Тогда ∠ АСО=180°-(90°+42°)=48°

2 вариант (30мин)

1. Отрезок BD является биссектрисой треугольника ABC. Найдите DC, если АВ = 30, AD = 20, ВС= 16.

2. Серединный перпендикуляр к стороне ВС треугольника ABC пересекает сторону АС в точке D. Найдите: АС, если BD = 11,4 AD=3,2 см.

3. Медиана AM треугольника ABC равна отрезку ВМ. Докажите, что один из углов треугольника ABC равен сумме двух других углов.

4. Острые углы прямоугольного треугольника равны и . Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.

1.

Ответ:

2.

3. АВМ- равнобедренный треугольник, потому что вм= ма, тогда ∠ 1 = ∠ 2.
АМС– равнобедренный треугольник, потому что ам= мс, тогда ∠ 3 = ∠ 4.

4. Пусть — высота, проведенная из вершины прямого угла , — биссектриса угла . Тогда
. Угол между высотой и биссектрисой — это угол . Ответ: .

3 вариант (30мин)

1. Биссектрисы АА1 и ВВ1 треугольника ABC пересекаются в точке М. Найдите углы ACM и ВСМ, если: ∠ AMB = 136°

2. Серединный перпендикуляр к стороне АВ равнобедренного треугольника ABC пересекает сторону ВС в точке Е. Найдите основание АС, если периметр треугольника ABC равен 27 см, а АВ=18 см.

3. В равнобедренном треугольнике ABC с основанием АС проведена медиана BD. На сторонах АВ и СВ отмечены соответственно точки E и F так, что АЕ=CF. Докажите, что: a) ΔBDE = ΔBDF; б) ΔADE=ΔCDF.

4. Два угла треугольника равны и . Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.

1. Дано: Найти: Ответ:

2.

3.

4. Из треугольника (угол — прямой) найдем угол . Он равен . Из треугольника ( — прямой) найдем угол . Он равен . В треугольнике известны два угла. Найдем третий, то есть угол , который и является тупым углом между высотами треугольника : . Ответ: .

Итог урока (2мин)

Время закончилось, собираем работы.

— какие задачи показались вам трудными? Что не получилось? ∆АВС, АК и В D – высоты треугольника АВС, пересекающиеся в точке О, ∠ САВ = 42 Найти: ∠ АСО.

Дети собирают контрольные работы, и обсуждают свои работы с учителем.

[2] ∠ АСО. Дано: ∆АВС, АК и В D – высоты треугольника АВС, пересекающиеся в точке О, ∠ САВ = 42 Найти:

🔍 Видео