Найдите неизвестные элементы треугольника если

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

1. Три стороны треугольника.
2. Две стороны треугольника и угол между ними.
3. Две стороны и угол противостоящий к одному из этих сторон треугольника.
4. Одна сторона и любые два угла.

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Видео:Найдите сторону треугольника на рисункеСкачать

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

(1)

(2)

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

.

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

.

.

, .

И, наконец, находим угол C:

Видео:Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:

.

.

Далее, из формулы

.

.

(3)

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

.

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

,

.

Из формулы (3) найдем cosA:

.

Поскольку уже нам известны два угла то находим третий:

.

Видео:9 класс, 15 урок, Решение треугольниковСкачать

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:

.

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

, .

, .

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Найдите неизвестные элементы треугольника ABC, если : a = 2, 4, b = 1, 3, угол С = 30°?

Геометрия | 5 — 9 классы

Найдите неизвестные элементы треугольника ABC, если : a = 2, 4, b = 1, 3, угол С = 30°.

Ответ : c ≈ 1, 4∠A ≈ 96°∠B ≈ 54°Объяснение : По теореме косинусов : c² = a² + b² — 2ab·cosCcos30° ≈ 0, 866c² ≈ 2, 4² + 1, 3² — 2 · 2, 4 · 1, 3 · 0, 866 ≈ 5, 76 + 1, 69 — 5, 4 ≈ 2, 05c ≈ 1, 4Углы можно найти по теореме синусов.

По синусу угла нельзя определить, острый он или тупой, поэтому применяем теорему для меньшей стороны (если тупой угол есть, то он лежит против большей стороны).

По теореме синусов : $dfrac=dfrac$$sinB=dfracapprox dfracapprox0,8041$∠B ≈ 54°Сумма углов треугольника 180°.

∠А = 180° — (∠B + ∠C) ≈ 180° — (54° + 30°) ≈ 180° — 84° ≈ 96°.

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Найдите неизвестные линейные элементы прямоугольного треугольника ABC (угол С = 90 градусов)?

Найдите неизвестные линейные элементы прямоугольного треугольника ABC (угол С = 90 градусов).

Дано : треугольник АВС,.

Видео:Теорема косинусов. Решить задачи. Найти сторону по двум сторонам и углу. Найти угол по сторонам.Скачать

В треугольнике АВС угол А равен 40 градусов, угол С равен 75 градусов, ВС равен 17?

В треугольнике АВС угол А равен 40 градусов, угол С равен 75 градусов, ВС равен 17.

Найдите неизвестные элементы треугольника.

Видео:Геометрия 9 класс (Урок№17 - Решение треугольников. Измерительные работы.)Скачать

В треугольнике CDE угол C = 64 градуса, угол D = 50 градусов, DE + CE = 21?

В треугольнике CDE угол C = 64 градуса, угол D = 50 градусов, DE + CE = 21.

Найдите неизвестные элементы треугольника.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

В треугольнике ABC a + b = 21, угол A = 64 градуса, угол B = 50 градусов ?

В треугольнике ABC a + b = 21, угол A = 64 градуса, угол B = 50 градусов .

Найдите неизвестные элементы треугольника.

Видео:9 класс. Геометрия. Решение треугольниковСкачать

В прямоугольном треугольнике ABC угол C = 90 градусов, угол B = 60 градусов, катет CB = 15см ?

В прямоугольном треугольнике ABC угол C = 90 градусов, угол B = 60 градусов, катет CB = 15см .

Найдите неизвестные элементы треугольника.

Видео:Нахождение стороны прямоугольного треугольникаСкачать

Найдите неизвестный угол треугольника, abc если известны его два угла 1?

Найдите неизвестный угол треугольника, abc если известны его два угла 1.

Видео:Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать

Найдите неизвестные углы каждого из треугольников ABC ?

Найдите неизвестные углы каждого из треугольников ABC :

Видео:Признаки равенства треугольников. 7 класс.Скачать

Найдите неизвестные элементы прямоугольного треугольника acd угол d = 90°, если ac = 4 угол, a = 60?

Найдите неизвестные элементы прямоугольного треугольника acd угол d = 90°, если ac = 4 угол, a = 60.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Найдите неизвестные углы треугольника а ABC если угол Б равен 25° внешне угол при вершине c равен 136?

Найдите неизвестные углы треугольника а ABC если угол Б равен 25° внешне угол при вершине c равен 136.

Видео:Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

В треугольнике ABC угол С равен 30 градусам, а внешний угол при вершине А равен 120 градусам?

В треугольнике ABC угол С равен 30 градусам, а внешний угол при вершине А равен 120 градусам.

Найдите неизвестные углы треугольника.

Перед вами страница с вопросом Найдите неизвестные элементы треугольника ABC, если : a = 2, 4, b = 1, 3, угол С = 30°?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

По теореме об отношении площадей подобных треугольников знаем, что площади подобных треугольников относятся, как k² = >² = > Но так как площадь хотя бы одно треугольника неизвестна, то задача дальше не решается.

1 задание 1) + 2) — 3) — 4) + 5) + 6) — 7) + 8) — 2 — 3 задание На фото.

Решение — в приложении.

Сумма внутреннего и внешнего углов равна 180° Находим внутренний угол при вершине b (т. Е. ∠abc) : 180 — 140 = 40° Поскольку треугольник abc — равнобедренный, следовательно углы при основании равны, следовательно∠abc = ∠acb = 40°.

Tgα = ВД(высоты) / 0, 5 * АС⇒10 / 7 = ВД / 14 ВД(высота) = 10 * 14 / 7 = 20⇒Sавс = 1 / 2 * 28 * 20 = 280.

1) 6 : 2 = 3 см — середина АВ и середина СD , так как они равны. 6 см + 3 см + 3 см = 12 см Ответ : 12 см 2) Не знаю как решать , извини. 3) Возьмем АВ за х AM = MB = x 2 Тогда MN = BN = MB 2 = x 4 AM : MN = x 2 : x 4 = 2 : 1 BN : AM = x ..

SΔ = (a * ha) / 2 SΔ = (14 * 6) / 2 = 42 см².

По твоему чертежу, но без окружности : А 0 — центр окружности I А0 — радиус I 0В — радиус I 0С — радиус I0___________C ∠А0С = ∠В0С = 90° I Соедини· А и· С I Получим равнобедренныйΔ А0С I А0 = 0С (это радиусы) I В равнобедренномΔ углы при основании B ..

1)х + х + 160 = 180 2х = 20 х = 10 2)160 + 10 = 170.

Видео:Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

Найти неизвестный элемент треугольника

Видео:Короткие загадки, которые осилит не каждый профессорСкачать

Решение задач по математике онлайн

Видео:Решение треугольников. Измерительные работыСкачать

Калькулятор онлайн.
Решение треугольников.

Решением треугольника называется нахождение всех его шести элементов (т.е. трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.

Эта математическая программа находит сторону ( c ), углы ( alpha ) и ( beta ) по заданным пользователем сторонам ( a, b ) и углу между ними ( gamma )

Программа не только даёт ответ задачи, но и отображает процесс нахождения решения.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Введите стороны ( a, b ) и угол между ними ( gamma ) Решить треугольник

Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

1. Три стороны треугольника.
2. Две стороны треугольника и угол между ними.
3. Две стороны и угол противостоящий к одному из этих сторон треугольника.
4. Одна сторона и любые два угла.

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Видео:Математика это не ИсламСкачать

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

(1)

(2)

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

.

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

.

.

, .

И, наконец, находим угол C:

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:

.

.

Далее, из формулы

.

.

(3)

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

.

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

,

.

Из формулы (3) найдем cosA:

.

Поскольку уже нам известны два угла то находим третий:

.

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:

.

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

, .

, .

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

Элементы треугольника — формулы вычисления основных параметров

Общие сведения

Произвольное множество точек называют геометрической фигурой. На плоскости они соединены замкнутыми линиями, образующими контур тела. В трёхмерном пространстве многоугольник, состоящий из трёх отрезков, не принадлежащих одной прямой, носит имя треугольник. Его линии называют сторонами или боковыми гранями, а место их пересечения — вершинами.

Треугольник — замкнутое геометрическое тело, состоящее из трёх сторон и такого же количества углов. Боковые грани принято обозначать маленькими латинскими буквами. Углы на рисунке показывают маленькой дугой, а в записи — символом ∠ с указанием соответствующей вершины. Точки же пересечения линий подписывают большими буквами.

Например, если имеется треугольник ABC, у него есть углы A, B, C и стороны a, b, c. Боковые грани могут обозначать и как отрезки, тогда в их имени учитываются ограничивающие точки. Например, AB, BC, CA. Строгого требования в виде обозначений нет, но существуют негласные правила, которых всё же рекомендуется придерживаться.

Хотя определение треугольника и его элементов одинаковое, выделяют 3 класса фигур:

• остроугольный — любой из углов тела не превышает 90 градусов;
• тупоугольный — форма одного из разворотов тупоугольная;
• прямоугольный — размер одного из трёх углов составляет 90 градусов.

Кроме этого, многоугольник классифицируют по числу равных сторон. Разносторонним он считается в том случае, если все они разной длины, равнобедренным — треугольник, имеющий 2 равные стороны, а равносторонним — у которого все стороны равны. Последний в литературе может ещё называться правильным.

На основании классификационных групп треугольники можно сравнивать между собой. Они считаются подобными, если 2 угла одного соответственно равны двум углам другого, или когда 2 стороны одного пропорциональны двум сторонам другого, а углы, заключённые между этими сторонами, равны. Эти правила называют признаками подобия. Они особенно популярны среди физиков. Их часто используют при вычислении элементов прямоугольников, квадратов, трапеций.

Элементы треугольника

Кроме сторон и вершин, фигура имеет различные точки и линии, называемые замечательными. Такое имя они получили из-за своих свойств. Но перед тем как их перечислить, нелишним будет привести основные величины, характеризующие фигуру, способы их нахождения и теоремы.

Периметр многоугольника можно определить, сложив все стороны: P = a + b + c. Площадь треугольника находится как половина произведения двух граней, умноженных на синус угла между ними: S = (a * b * sinC) / 2. Сумма углов равна 180 градусов, при этом напротив равных сторон лежат одинаковые углы.

К замечательным линиям относят:

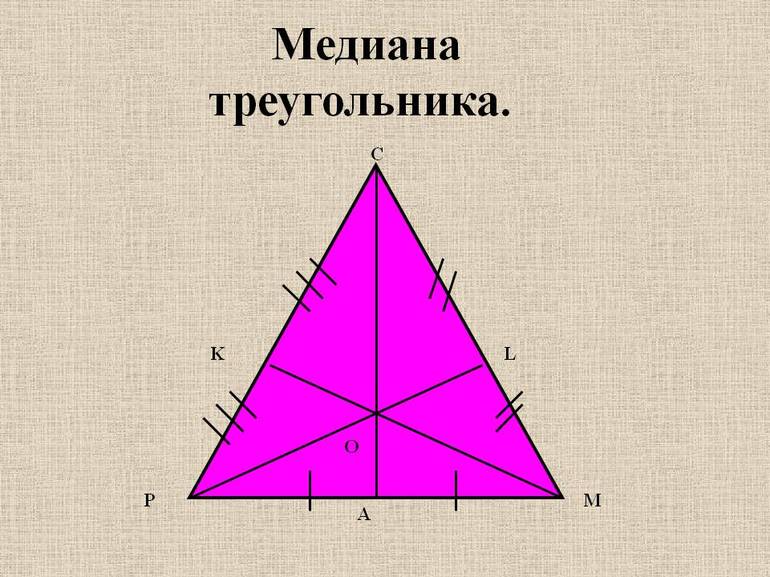
1. Медиану — линию, проходящую через вершину к середине противолежащей стороны. Всего в треугольнике можно провести 3 таких отрезка. Точка их пересечения является центром массы. Если считать от вершины, в ней она делится в отношении 2 к 1. Каждая медиана разделяет фигуру на 2 объекта с одинаковой площадью.
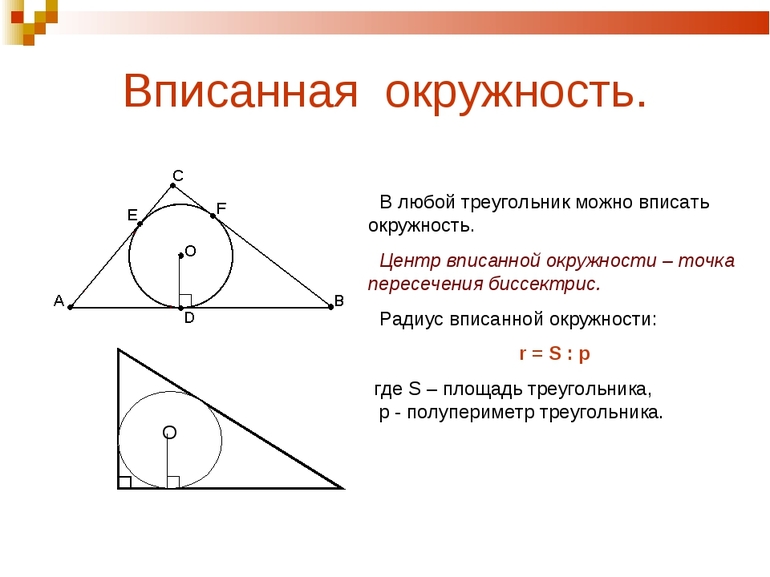
2. Биссектрису — отрезок, построенный к стороне из угла и делящий его на 2 равные части. Она делит грань на 2 замкнутые линии, пропорциональные прилежащим сторонам. Точка, в которой пересекаются биссектрисы, является началом диаметра вписанной в треугольник окружности.
3. Высоту — перпендикуляр, опущенный из угла на противоположную сторону. Все они пересекаются в одной точке.
4. Срединную линию — проходит всегда параллельно одной из граней и соединяет середины двух оставшихся сторон. 3 таких линии разделят многоугольник на 4 равных треугольника.

При измерениях используют и «особенные» точки фигуры. Если в треугольник вписать окружность, её центр совпадёт с местом скрещивания перпендикуляров. А если поместить в круг, середина будет совпадать с пересечением биссектрис. Для других замечательных линий точки их соприкосновения также имеют свои названия: ортоцентр (высот) и центроид (медиан). Первая может принадлежать как внутренней площади фигуры, так и внешней (тупоугольный треугольник).

В равнобедренном треугольнике медиана, высота и биссектриса совпадают. При этом их центр является серединой как вписанной окружности, так и описанного круга. А угол, из которого построен один из таких отрезков, будет разделён на 2 одинаковых разворота равных 30 градусам.

Основные формулы

Найти любой элемент треугольника можно по специальным формулам. Чаще всего приходится искать стороны фигуры. Зная их, можно найти практически любые параметры, просто подставив в выражения значения размеров граней.

Найти длину отрезка, формирующего контур фигуры, можно, зная длины двух сторон и угла или значения двух углов и одной стороны. Для первого случая формула имеет вид a = b * sin (a) / sin (b) = b * sin (a) / sin (a + c), а второго: a = √(b 2 + c 2 — 2bc * cos (a)). Если имеется тупой угол, косинус будет отрицательный. Это необходимо учитывать при расчётах.

Это общие формулы, подходящие для любого типа треугольника. Но в то же время для прямоугольного существует своё правило, связывающее все 3 грани в одну формулу: c = √(b 2 + a 2 ). Называется оно теоремой Пифагора. В равнобедренном вычислить сторону можно, зная любую другую и угол. Для основания используют равенство b = 2a * cos (a), а для равных граней: a = b / 2 * cos (a).

Из множества других существующих формул для определения различных элементов фигуры, можно указать на те, что чаще всего используются при решении примеров:

1. Высота: h = (2 / a) * √(p * (p — a) * (p — b) * (p — c)) или h = b * sin© = c * sin (b). Отрезок можно найти, зная площадь и сторону h = 2 * S / a или радиус описанной окружности: h = (b * c) / 2 * R.
2. Биссектриса: L = √(a * b * (a + b + c) * (a + b — c)) / (a + b). Формулу можно упростить, используя периметр: L = 2 * √ (a * b * P) * (P — c)) / (a + b), где P = p /2 (полупериметр).
3. Медиана: М = √(2 * a 2 + 2b 2 — c 2 ) / 2. Линию можно определить, зная только 2 стороны и лежащий между ними угол: М = √(a 2 + b 2 — 2 * a * b * cos (с)) / 2. В прямоугольном треугольнике она равняется радиусу описанного круга или половине гипотенузы: М = R = c / 2.

Существуют и упрощённые выражения. Формула Герона позволяет высчитать площадь, используя полупериметр и длины сторон: S = √(P * (P — a) * (P — b) * (P — c)). Также величину можно определить, зная высоту и длину основания: S = (a * H) / 2.

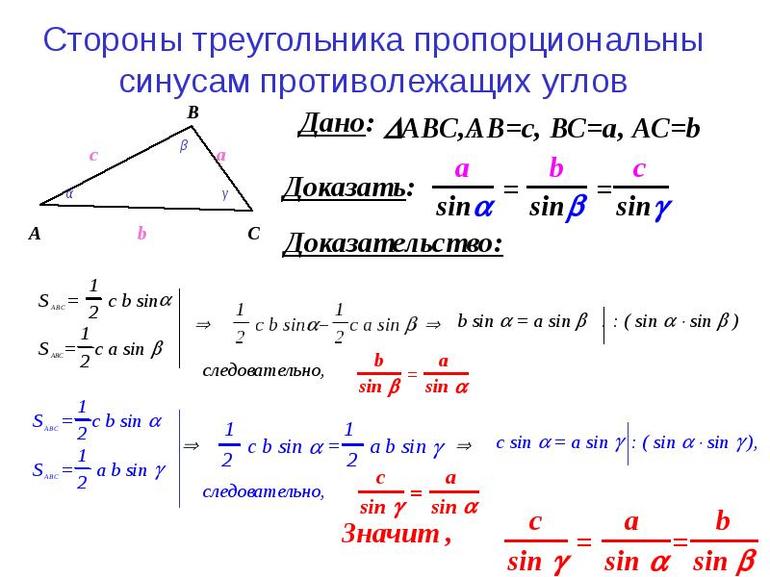
Для нахождения элементов треугольника в 7 классе ученикам дают ещё 2 фундаментальные теоремы: косинусов и синусов. Первая сообщает, что квадрат грани фигуры равен удвоенному произведению двух сторон и косинуса угла между ними, вычтенному из сумы квадратов: a 2 = b 2 + c 2 — 2 * b * c * cos (a). Согласно же второй, стороны пропорциональны синусам противолежащих углов: a / sin (a) = b / sin (b) = c / sin©.

Решение примеров

Формул для вычисления элементов треугольников можно насчитать несколько десятков. Запомнить их довольно сложно, поэтому нужно выучить основные определения и выражения, а сделать это лучше всего, решая практические примеры. Вот некоторые из них:

1. В треугольнике проведено 2 высоты. Одна равняется 63 см, а другая 56 см. Найти истинный отрезок, если основание AC = 84 см, а размер медианы BK совпадает с длиной стороны BC. Так как точка K делит отрезок AC пополам, AK = KC = AC / 2 = 84 /2 = 42 см. В треугольнике BKC 2 стороны равны друг другу, согласно условию, значит, он равнобедренный. Следовательно, высота является одновременно и медианой. KH = HC = MC /2 = 42 / 2 = 21 см. Искомый отрезок будет равен: h = AK + KC = 42 + 21 = 63 см. Следовательно, правильный первый вариант.
2. Пусть дан треугольник ABC. Найти возможный отрезок BN, на который биссектриса поделит сторону BC, если AB = 6 см, BC = 7 см, AC = 8 см. Для решения понадобится вспомнить свойство биссектрисы. Из него следует, что BN / NC = AB / AC = 6 / 8. Если искомый отрезок принять за икс, будет верным равенство KC = 7 — x. Значит: x / (7 — x) = 6 / 8. Отсюда можно выразить неизвестное: x = 42 / 14 = 3 см. Теперь останется подставить найденное число и найти искомое значение: KC = 7 — 3 = 4 см.
3. Завод начал выпускать новую серию объёмных фигур. Определить, какой тип многоугольника лежит в их основании, если её стороны равны 3, 2 и √3. Чтобы найти ответ, нужно проанализировать исходные данные. Так как сумма двух меньших сторон больше третей боковой грани, в основании лежит треугольник. 3 в квадрате не равно 2 2 + (√3) 2 . Следовательно, геометрическое тело непрямоугольное. По теореме косинусов можно записать: a 2 = b 2 + c 2 — 2 * b * c * cos (a). Исходя из того, что cos (a) = -1/ √ 3, то есть он отрицательный, можно утверждать, что разворот угла тупой. Значит, треугольник у основания тупоугольный.

Проверить правильность вычислений можно, воспользовавшись онлайн-калькуляторами. Это сервисы, предоставляющие услуги по расчёту различных математических величин. Воспользоваться ими сможет любой, даже тот, кто не знает ни одной формулы и теоремы. Всё, что требуется от пользователя — правильно ввести исходные данные в специальную форму и нажать кнопку «Рассчитать». Через несколько секунд ответ, а в некоторых случаях и решение, появится на экране.