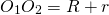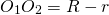Общие касательные к двум окружностям
 Взаимное расположение двух окружностей |
| Общие касательные к двум окружностям |
| Формулы для длин общих касательных и общей хорды |
| Доказательства формул для длин общих касательных и общей хорды |
Видео:9 класс, 8 урок, Взаимное расположение двух окружностейСкачать
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
| ||
| Внешнее касание двух окружностей | ||
| ||
| Внутреннее касание двух окружностей | ||
| ||
| Окружности пересекаются в двух точках | ||
| ||
| ||
| Каждая из окружностей лежит вне другой | ||
Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
| |
| Внутреннее касание двух окружностей | |
| |
| Окружности пересекаются в двух точках | |
| |
| Внешнее касание двух окружностей | |
| |
| |
| Каждая из окружностей лежит вне другой | |
| |
| Внешняя касательная к двум окружностям | |||||||||||||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||||||||||||
| Внутреннее касание двух окружностей | |||||||||||||||||||||
| Окружности пересекаются в двух точках | |||||||||||||||||||||
| Внешнее касание двух окружностей | |||||||||||||||||||||
| Каждая из окружностей лежит вне другой | |||||||||||||||||||||
| Фигура | Рисунок | Формула | ||||||||||||
| Внешняя касательная к двум окружностям |  | |||||||||||||
| Внутренняя касательная к двум окружностям |  | |||||||||||||
| Общая хорда двух пересекающихся окружностей |  | |||||||||||||
| Внешняя касательная к двум окружностям | ||||
| ||||
| Внутренняя касательная к двум окружностям | ||||
| ||||
| Общая хорда двух пересекающихся окружностей | ||||
| ||||
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
Длина общей хорды двух окружностей вычисляется по формуле
Видео:Взаимное расположение двух окружностей. Урок 8. Геометрия 9 классСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле
Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Взаимное расположение окружностей. Практическая часть. 7 класс.Скачать  Взаимное расположение окружностейВыясним, каким может быть взаимное расположение двух окружностей. Две окружности могут пересекаться, не пересекаться либо касаться друг друга. I. Пересекающиеся окружности имеют две общие точки.
Расстояние между центрами двух пересекающихся окружностей больше разности, но меньше суммы их радиусов:
II. Не пересекающиеся окружности не имеет общих точек.
Если одна окружность лежит внутри другой, то расстояние между центрами меньше разности их радиусов:
III. Касающиеся окружности имеют одну общую точку — точку касания.
При внешнем касании расстояние между центрами окружностей равно сумме их радиусов:
При внутреннем касании расстояние между центрами равно разности радиусов:
Концентрические окружности разного радиуса не пересекаются. Расстояние между центрами концентрических окружностей равно нулю: O1O2=0. Видео:Взаимное расположение окружностей. 7 класс.Скачать  Геометрия. 9 классДве окружности могут пересекаться, не пересекаться либо касаться друг друга. Если одна окружность лежит внутри другой, то расстояние между центрами меньше разности их радиусов: Кольцом называют фигуру, заключенную между концентрическими окружностями. Видео:Взаимное расположение двух окружностейСкачать  НАШИ ПАРТНЁРЫ
© Государственная образовательная платформа «Российская электронная школа» 🌟 ВидеоТеорема о числе точек пересечения двух окружностейСкачать  УЧИМ ВМЕСТЕ (ВОЛШЕБНАЯ ГЕОМЕТРИЯ).Скачать  Общая хорда двух окружностейСкачать  Взаимное расположение двух окружностейСкачать  Взаимное расположение двух окружностей.Использование уравнений окружности и прямой при решении задачСкачать  Взаимное расположение двух окружностейСкачать  Пересечение двух окружностейСкачать  Взаимное расположение прямой и окружности Взаимное расположение двух окружностейСкачать  Пересечение двух окружностейСкачать  Геометрия 16-09. Взаимное расположение двух и более окружностей. Задача 9Скачать  1 2 4 сопряжение окружностейСкачать  взаимное расположение двух окружностей.(не пересекаются)Скачать  Алгоритмы. Пересечение окружностейСкачать  7 класс. Геометрия. Взаимное расположение двух окружностей.Скачать  |
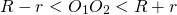
Если одна окружность находится вне другой, расстояние между центрами больше суммы их радиусов: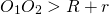
R + r]» title=»Rendered by QuickLaTeX.com»/>
