Центробежная сила при движении по окружности (6 видео)

Центробежная сила

Сегодня среди специалистов укрепилось мнение, что из двух составляющих криволинейного движения, частным случаем которого является вращательной движение, реальной является только центростремительная сила, а центробежная — это некая математическая фикция, являющеюся силой виртуальной. При этом реальный опыт во внимание не принимается.
Корни этого положения вещей кроются в фундаментальных ошибках Ньютона, одна из которых касается понимания природы центростремительной силы.

Отрывая свой труд «Материалистические начала натуральной философии» 1686 года Исаак Ньютон предваряет его описанием терминов, которые он использует в своей работе. Так на странице 26 [1] читаем:

«Центростремительная сила есть та, с которою тела к некоторой точке, как центру, отовсюду притягиваются, гонятся или как бы то ни было стремятся.
Такова сила тяжести, под действием которой тела стремятся к центру Земли; магнитная сила, которою железо притягивается к магниту, и та сила, каковою бы она не была, которые планеты постоянно отклоняются от прямолинейного движения и вынуждаются обращаться по кривым линиям…»

Здесь Ньютон достаточно не двусмыслено определяет центростремительную силу, как некую внешнюю силу действующую на тела и заставляющюю их изменять свое прямолинейное джижение в соответствии с его первым законом механики на криволинейное движение. Здесь важно отметить, что под центростремительной силой Ньютон понимает именно силу, а не просто препятствие прямолинейному движению.

Но вот то, что он пишет далее является одной из его фундаментальных ошибок определившей судьбу центробежной силы:

«Камень, вращаемый в праще, стремится удалиться от вращающей пращу руки, и этим свои стремлением натягивает пращу тем сильнее, чем сильнее вращение, и как только его пустят, то камень улетает.
Силу, противоположную сказанному стремлению, которою праща постоянно оттягивает камень к руке и удерживает его на круге, т.е. силу направленную к руке или к центру описываемого круга, я называю центростремительной. Это относится и до всякого тела, движущегося по кругу.»

Здесь Ньютон становится заложником логического принципа «аналогия»: если гравитационная и магнитная сила являются центростремительными, то и любое непрерывное ограничение прямолинейного движения является силой.
Если в отношении гравитационной и магнитной силы утверждение, что эти силы являются центростремительными, при определенных условиях, верно, то распространение этого утверждения на все случаи непрерывного ограничения прямолинейного движения является фундаментальной ошибкой Ньютона.
Праща, удерживающая камень на орбите вращения, не создает ни какой силы, а лишь препятствует прямолинейному движению камня. Это доказывается тем, что сила, которая натягивает пращу, пропорциональна угловой скорости вращения, и если бы существовала аналогичная центростремительная сила, то тело бы, сколько не увеличивай скорость вращения, всегда оставалось бы в равновесии, так как пропорционально этому увеличивалась бы и центростремительная сила. Но при достижении определенной скорости вращения, если прочность материала пращи будет недостаточна, она рвется и камень уходит с орбиты, но не в сторону центра, а в противоположную. Причём не по касательной как многие считают, а под углом к ней в 54,74 градуса.
Если бы Ньютон, провел опыт с телом, свободно передвигающимся по вращающемуся штоку, то увидел бы, что тело это всегда стремится от центра к периферии и никогда обратно. Если не ограничивать тело на концах штока, то оно всегда уходит с орбиты вращения. Это указывает на то, что на тело во время вращения действует, лишь одна сила, направленная в противоположную от центра вращения сторону, а центростремительной силы в пассивных связях физически не существует. Поэтому отождествлять реакцию кинематической связи с центростремительной силой в корне не верно.

Сделав эту фундаментальную ошибку, Ньютон вновь возвращается к рассмотрению центростремительной силы тождественной гравитационному и магнитному взаимодействию, тем самым дав понять, что кинематическая связь во вращательном движении и собственно источники центростремительной силы суть одно и тоже, закрепив в сознании своих последователей искаженное понимание природы центростремительной силы. Так на странице 81 [1] он пишет в отношении тела вращающегося внутри круга:

«Такова центробежная сила, с которою тело давит на круг; ей равна и противоположна сила, с которою круг отталкивает тело к своему центру.»

Здесь мы уже видим приложение четвертого следствия третьего закона Ньютона: у любого действия есть равное и обратно направленное противодействие.
Ложность этого утверждения показана мною в статье «Третий закон Ньютона».
В рассмотренном случае в отсутствии природной центростремительной силы (гравитационной, магнитной или иной аналогичной) круг лишь ограничивает движение тела под действием центробежной силы, но сам при этом никакой силы не создает.

На странице 513 [1] Ньютон достаточно витиевато объясняет, что основной причиной, по которой Луна находится на своей орбите, есть равенство центростремительной и центробежной силы. Причем в качестве центростремительной силы Ньютон рассматривает силу тяжести, или как мы её теперь называем силу гравитационного взаимодействия.
Этим утверждением Ньютон фактически признает, что при наличии двух равных по модулю и противоположных по направлению сил вращательного движения, тело находится в равновесии неограниченно долго. Поэтому если в связке двух тел отсутствует центростремительная сила, то тело сателлит, которое движется вокруг центра вращения, будет находиться под действием всего одной физически реальной силы — центробежной. В связи с этим для того чтобы удержать его на стационарной орбите нужна кинематическая связь, позволяющая сохранять расстояние между телами постоянным. При этом следует помнить, что эта связь, также как и тело-сателлит будет находиться под воздействием центробежной силы со всеми вытекающими из этого последствиями.

Далее Ньютон рассматривает различие природы центростремительной силы, в качестве которой выступает гравитация, и центробежной силы.
Гравитационная сила всегда направлена к центру Земли, поэтому её значение в любом месте на поверхности Земли одинаково.* А вот центробежная сила зависит от расстояния рассматриваемой точки до оси вращения Земли, и чем дальше от полюсов, тем больше его значение. В связи с этим вес тела у полюса будет больше чем на экваторе. Этого не могло бы произойти, если бы центростремительная сила находилась в той же плоскости, что и центробежная, и зависела от параметров вращательного движения. Отсюда мы можем сделать один единственный вывод, что центростремительная сила (именно сила) является особого рода природной силой и зависящей исключительно от расстояния между телами, а не от угловой скорости тела-сателлита.
Этот вывод подтверждает и собственно форма Земли – сплюснутый эллипсоид, образовавшийся благодаря тому, что в природе не существует центростремительной силы, в том виде, в каком её представляет Ньютон вне действия природных сил взаимодействия материальных тел (гравитационных, магнитных и аналогичных).

Таким образом, вращательное (криволинейное) движение является уравновешенным в двух совершенно разных случаях:
1. В качестве центростремительной силы выступает некая природная сила, характер которой не зависит от скорости движения тела-сателлита по криволинейной траектории. В качестве такой силы может выступать гравитационная, магнитная или аналогичная им сила.
2. Вращательное (криволинейное) движение осуществляется исключительно под воздействием центробежной силы, действие которой ограничивается кинематической связью, которая в свою очередь, так же находится под её воздействием. В этом случае, ни какой центростремительной силы в криволинейном движении нет.

1. Ньютон Исаак. Математические начала натуральной философии. — М.: Наука, 1989. Перепечатка с VII тома собрания трудов академика А.Н. Крылова, его собственного перевода. М.-Л.: изд. АН СССР, 1936.
* Эта одинаковость условна в определенных границах.

Содержание

Вращательное движение
1. Равномерное вращательное движение
2. Центробежное ускорение
3. Центробежная сила
4. Градусы и радианы
Центробежная сила
📸 Видео

Видео:Движение тел по окружностиСкачать

Вращательное движение

Ранее рассматривались характеристики прямолинейного движения: перемещение, скорость, ускорение. Их аналогами при вращательном движении являются: угловое перемещение, угловая скорость, угловое ускорение.

Роль перемещения во вращательном движении играет угол;
Величина угла поворота за единицу времени — это угловая скорость;
Изменение угловой скорости за единицу времени — это угловое ускорение.

1. Равномерное вращательное движение

Во время равномерного вращательного движения тело совершает движение по окружности с одинаковой скоростью, но с изменяющимся направлением. Например, такое движение совершают стрелки часов по циферблату.

Допустим, шар равномерно вращается на нити длиной 1 метр. При этом он будет описывать окружность с радиусом 1 метр. Длина такой окружности: C = 2πR = 6,28 м

Время, за которое шар полностью делает один полный оборот по окружности, называется периодом вращения — T.

Чтобы вычислить линейную скорость шара, необходимо разделить перемещение на время, т.е. длину окружности на период вращения:

Если наш шар будет делать один оборот за 1 секунду (период вращения = 1с), то его линейная скорость:
V = 6,28/1 = 6,28 м/с

2. Центробежное ускорение

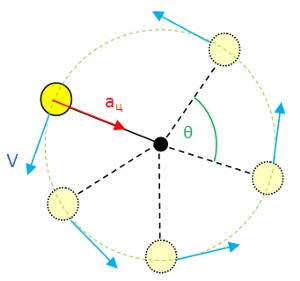
В любой точке вращательного движения шара вектор его линейной скорости направлен перпендикулярно радиусу. Нетрудно догадаться, что при таком вращении по окружности, вектор линейной скорости шара постоянно меняет свое направление. Ускорение, характеризующее такое изменение скорости, называется центробежным (центростремительным) ускорением.

Составляющая вектора скорости, перпендикулярная радиусу вращения, является касательной к траектории движения и называется тангенциальной составляющей. Перпендикулярная ей компонента называется нормальной составляющей

Во время равномерного вращательного движения меняется только направление вектора скорости, но не величина! Поэтому линейное ускорение = 0. Изменение линейной скорости поддерживается центробежным ускорением, которое направлено к центру окружности вращения перпендикулярно вектору скорости — a_ц.

Центробежное ускорение можно вычислить по формуле: a_ц = V 2 /R

Чем больше линейная скорость тела и меньше радиус вращения, тем центробежное ускорение больше.

3. Центробежная сила

Из прямолинейного движения мы знаем, что сила равна произведению массы тела на его ускорение.

При равномерном вращательном движении на вращающееся тело действует центробежная сила:

Если наш шарик весит 1 кг, то для удержания его на окружности понадобится центробежная сила:

F_ц = 1·6,28 2 /1 = 39,4 Н

С центробежной силой мы сталкиваемся в повседневной жизни при любом повороте.

Задача №1: расчитать, какую максимальную скорость может развить тело в повороте с радиусом 30 метров при коэффициенте трения 0,9, чтобы «вписаться» в этот поворот.

Сила трения должна уравновесить центробежную силу:

V = √μmgR/m = √μgR = √0,9·9,8·30 = 16,3 м/с = 58,5 км/ч

Ответ: 58,5 км/ч

Обратите внимание, что скорость в повороте не зависит от массы тела!

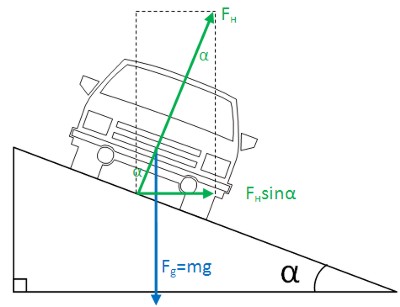
Наверняка вы обращали внимание, что некоторые повороты на шоссе имеют некоторый наклон внутрь поворота. Такие повороты «легче» проходить, вернее, можно проходить с бОльшей скоростью. Рассмотрим какие силы действуют на автомобиль в таком повороте с наклоном. При этом силу трения учитывать не будем, а центробежное ускорение будет компенсироваться только горизонтальной составляющей силы тяжести:

В вертикальном направлении на тело действует сила тяжести F_g = mg, которая уравновешивается вертикальной составляющей нормальной силы F_нcosα:

F_нcosα = mg , отсюда: F_н = mg/cosα

Подставляем значение нормальной силы в исходную формулу:

F_ц = F_нsinα = (mg/cosα)sinα = mg·sinα/cosα = mg·tgα

Т.о., угол наклона дорожного полотна:

α = arctg(F_ц/mg) = arctg(mV 2 /mgR) = arctg(V 2 /gR)

Опять обратите внимание, что в расчетах не участвует масса тела!

Задача №2: на некотором участке шоссе имеется поворот с радиусом 100 метров. Средняя скорость прохождения этого участка дороги автомобилями 108 км/ч (30 м/с). Каким должен быть безопасный угол наклона полотна дороги на этом участке, чтобы автомобиль «не вылетел» (трением пренебречь)?

α = arctg(V 2 /gR) = arctg(30 2 /9,8·100) = 0,91 = 42°

Ответ: 42°. Довольно приличный угол. Но, не забывайте, что в наших расчетах мы не принимаем во внимание силу трения дорожного полотна.

4. Градусы и радианы

Многие путаются в понимании угловых величин.

При вращательном движении основной единицей измерения углового перемещения является радиан.

2π радиан = 360° — полная окружность
π радиан = 180° — половина окружности
π/2 радиан = 90° — четверть окружности

Чтобы перевести градусы в радианы, необходимо значение угла разделить на 360° и умножить на 2π. Например:

45° = (45°/360°)·2π = π/4 радиан
30° = (30°/360°)·2π = π/6 радиан

Ниже в таблице представлены основные формулы прямолинейного и вращательного движения.

Прямолинейное движение	Вращательное движение
s — линейное перемещение V — линейная скорость a — линейное ускорение V = Δs/Δt a = ΔV/Δt s = V₀(t₁ — t₀) + sa(t₁ — t₀) 2 V₁ 2 — V₀ 2 = 2as	Θ — угловое перемещение ω — угловая скорость α — угловое ускорение ω = ΔΘ/Δt α = Δω/Δt Θ = ω₀(t₁ — t₀) + sα(t₁ — t₀) 2 ω₁ 2 — ω₀ 2 = 2αΘ

Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:

Код кнопки:
Политика конфиденциальности Об авторе

Видео:Физика - движение по окружностиСкачать

Центробежная сила

Вам, наверное, доводилось испытывать неприятные ощущения, когда машина, в которой вы едете, входила в крутой вираж. Казалось, что сейчас вас так и выбросит на обочину. И если вспомнить законы механики Ньютона, то получается, что раз вас буквально вдавливало в дверцу, значит на вас действовала некая сила. Ее обычно называют «центробежная сила». Именно из-за центробежной силы так захватывает дух на крутых поворотах, когда эта сила прижимает вас к бортику автомобиля. (Между прочим, этот термин, происходящий от латинских слов centrum («центр») и fugus («бег»), ввел в научный обиход в 1689 году Исаак Ньютон.)

Стороннему наблюдателю, однако, всё будет представляться иначе. Когда машина закладывает вираж, наблюдатель сочтет, что вы просто продолжаете прямолинейное движение, как это и делало бы любое тело, на которое не оказывает действия никакая внешняя сила; а автомобиль отклоняется от прямолинейной траектории. Такому наблюдателю покажется, что это не вас прижимает к дверце машины, а, наоборот, дверца машины начинает давить на вас.

Впрочем, никаких противоречий между этими двумя точками зрения нет. В обеих системах отсчета события описываются одинаково и для этого описания используются одни и те же уравнения. Единственным отличием будет интерпретация происходящего внешним и внутренним наблюдателем. В этом смысле центробежная сила напоминает силу Кориолиса (см. Эффект Кориолиса), которая также действует во вращающихся системах отсчета.

Поскольку не все наблюдатели видят действие этой силы, физики часто называют центробежную силу фиктивной силой или псевдосилой. Однако мне кажется, что такая интерпретация может вводить в заблуждение. В конце концов, едва ли можно назвать фиктивной силу, которая ощутимо придавливает вас к дверце автомобиля. Просто всё дело в том, что, продолжая двигаться по инерции, ваше тело стремится сохранить прямолинейное направление движения, в то время как автомобиль от него уклоняется и из-за этого давит на вас.

Чтобы проиллюстрировать эквивалентность двух описаний центробежной силы, давайте немного поупражняемся в математике. Тело, движущееся с постоянной скоростью по окружности, движется с ускорением, поскольку оно всё время меняет направление. Это ускорение равно v 2 /r, где v — скорость, а r — радиус окружности. Соответственно, наблюдатель, находящийся в движущейся по окружности системе отсчета, будет испытывать центробежную силу, равную mv 2 /r.

Теперь обобщим сказанное: любое тело, движущееся по криволинейной траектории, — будь то пассажир в машине на вираже, мяч на веревочке, который вы раскручиваете над головой, или Земля на орбите вокруг Солнца — испытывает на себе действие силы, которая обусловлена давлением дверцы автомобиля, натяжением веревки или гравитационным притяжением Солнца. Назовем эту силу F . С точки зрения того, кто находится во вращающейся системе отсчета, тело не движется. Это означает, что внутренняя сила F уравновешивается внешней центробежной силой:

Однако с точки зрения наблюдателя, находящегося вне вращающейся системы отсчета, тело (вы, мяч, Земля) движется равноускоренно под воздействием внешней силы. Согласно второму закону механики Ньютона, отношение между силой и ускорением в этом случае F = ma. Подставив в это уравнение формулу ускорения для тела, движущегося по окружности, получим:

Но тем самым мы получили в точности уравнение для наблюдателя, находящегося во вращающейся системе отсчета. Значит, оба наблюдателя приходят к идентичным результатам относительно величины действующей силы, хотя и исходят из разных предпосылок.

Это очень важная иллюстрация того, что представляет собою механика как наука. Наблюдатели, находящиеся в различных системах отсчета, могут описывать происходящие явления совершенно по-разному. Однако, сколь бы принципиальными ни были различия в подходах к описанию наблюдаемых ими явлений, уравнения, их описывающие, окажутся идентичными. А это — не что иное, как принцип инвариантности законов природы, лежащий в основе теории относительности.