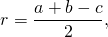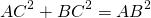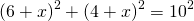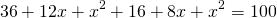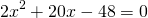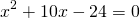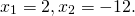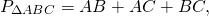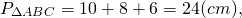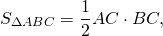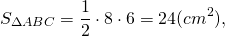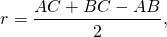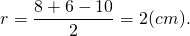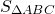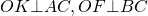Вписанная окружность в прямоугольный треугольник окружность делит гипотенузу

Окружность, вписанная в прямоугольный треугольник, делит точкой касания гипотенузу на отрезки 12 и 5. Найдите радиус окружности.

По свойству касательных, проведенных из одной точки: (AK=AN=12, CK=CM=5, BM=NB=R,) где (R) — радиус окружности.

По теореме Пифагора: (17^2=(5+R)^2+(12+R)^2) .

Тогда получаем квадратное уравнение (применим формулу сокращенного умножения квадрат суммы) относительно радиуса вписанной окружности, которое решаем при помощи дискриминанта и получаем корни.

(R^2+17R-60=0 Rightarrow R_1=3, R_2=-20.)

Второй корень не подходит, так как радиус — величина неотрицательная. Следовательно, ответ 3.

Видео:Геометрия Точка касания вписанной окружности делит гипотенузу прямоугольного треугольника на отрезкиСкачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:Геометрия Точка касания окружности, вписанной в прямоугольный треугольник, делит его гипотенузу наСкачать

Окружность, вписанная в прямоугольный треугольник

Если в задаче дана окружность, вписанная в прямоугольный треугольник, то ее решение может быть связано со свойством отрезков касательных, проведенных из одной точки, и теоремой Пифагора.

Кроме того, следует учесть, что радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле

где a и b — длины катетов, c — гипотенузы.

Рассмотрим две задачи на вписанную в прямоугольный треугольник окружность.

Точка касания окружности, вписанной в прямоугольный треугольник, делит гипотенузу на отрезки 4 см и 6 см. Найти периметр и площадь треугольника и радиус окружности.

Дано: ∆ ABC, ∠C=90º,

окружность (O, r) — вписанная,

K, M, F — точки касания со сторонами AC, AB, BC,

1) По свойству отрезков касательных, проведенных из одной точки,

AK=AM=6 см,

2) AB=AM+BM=6+4=10 см,

3) По теореме Пифагора:

Второй корень не подходит по смыслу задачи. Значит, CK+CF=2 см, AC=8 см, BC=6 см.

Ответ: 24 см, 24 см², 2 см.

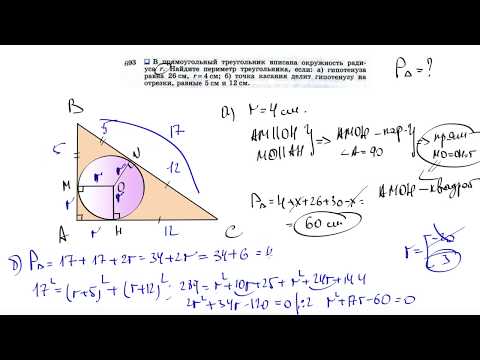
Найти площадь прямоугольного треугольника, гипотенуза которого равна 26 см, а радиус вписанной окружности — 4 см.

Дано:∆ ABC, ∠C=90º,

окружность (O, r) — вписанная,

K, M, F — точки касания со сторонами AC, AB, BC,

1) Проведем отрезки OK и OF.

(как радиусы, проведенные в точки касания).

Четырехугольник OKCF — прямоугольник (так как у него все углы — прямые).

А так как OK=OF (как радиусы), то OKCF — квадрат.

2) По свойству касательных, проведенных из одной точки,

3) AC=AK+KC=(x+4) см, BC=BF+CF=26-x+4=(30-x) см.

Видео:Г: В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5 12Скачать

Докажите, что вписанная в прямоугольный треугольник окружность делит гипотенузу на отрезки, произведение длин которых равно площади этого треугольника?

Геометрия | 5 — 9 классы

Докажите, что вписанная в прямоугольный треугольник окружность делит гипотенузу на отрезки, произведение длин которых равно площади этого треугольника.

Проведём три радиуса в точки касания.

Рассмотрим фигуру ODBF.

OD = OF, ∠ODB = ∠OFB = 90° (т.

К. радиус, проведённый в точку касания, перпендикулярен касательной) .

Тогда ODBF — квадрат⇒ OD = OF = BF = DB.

Выразим теперь площадь треугольника через радиус вписанной окружности и периметр :

$S_ = dfrac(AB + BC + AC) cdot r = \ \ = dfracOD cdot (AD + DB + BF + FC + EC + AE) = \ \ dfracOD( 2OD + 2AE + 2EC) =$

А теперь через катеты :

$S_ = dfracAB cdot BC = dfrac(AD + DB)(BF + FC) = \ \ = dfrac(DO + EC)(DO + AE) = \ \ = dfrac(DO^2 + DO cdot AE + EC cdot DO + EC cdot AE)$$= OD(OD + AE + EC) (1)$

Приравняем теперь две данные формулы площади :

$dfrac(DO^2 + DO cdot AE + EC cdot DO + EC cdot AE) = OD(OD + AE + EC) \ \ DO^2 + DO cdot AE + EC cdot DO + EC cdot AE = 2OD(OD + AE + EC) \ \ DO^2 + DO cdot AE + EC cdot DO + EC cdot AE = 2OD^2+ 2OD cdot AE + \ + 2OD cdot EC \ \ AE cdot EC = 2OD^2+ 2OD cdot AE + 2OD cdot EC — DO^2 — DO cdot AE — \ — EC cdot DO — EC cdot AE \ \ AE cdot EC = OD^2 + OD cdot AE + OD cdot EC \ \ AE cdot EC = OD(OD + AE + EC)$

Мы пришли к формуле (1), через которую находили площадь треугольника.

Значит, площадь прямоугольного треугольника равна произведению отрезков, на которые вписанная окружность делит гипотенузу.

Видео:Вписанная окружность. ЗАДАЧА ИЗ ГОНКОНГА!Скачать

В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна 26см, а длина вписанной окружности равна 16п см?

В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна 26см, а длина вписанной окружности равна 16п см.

Обчислиты площадь треугольника.

Видео:№693. В прямоугольный треугольник вписана окружность радиуса r. Найдите периметр треугольника,Скачать

Гипотенуза прямоугольного треугольника равна 16, а радиус вписанной окружности этого треугольника равен 3?

Гипотенуза прямоугольного треугольника равна 16, а радиус вписанной окружности этого треугольника равен 3.

Найдите периметр треугольника.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

В прямоугольном треугольнике сумма катетов равна 13 а радиус вписанной окружности равен 2 найдите длину гипотенузы?

В прямоугольном треугольнике сумма катетов равна 13 а радиус вписанной окружности равен 2 найдите длину гипотенузы.

Видео:Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать

В прямоугольный треугольник вписана окружность радиус которой равен 3 см Вычислите периметр треугольника если его гипотенуза равно 20см ?

В прямоугольный треугольник вписана окружность радиус которой равен 3 см Вычислите периметр треугольника если его гипотенуза равно 20см .

Видео:№694. Найдите диаметр окружности, вписанной в прямоугольный треугольник, если гипотенузаСкачать

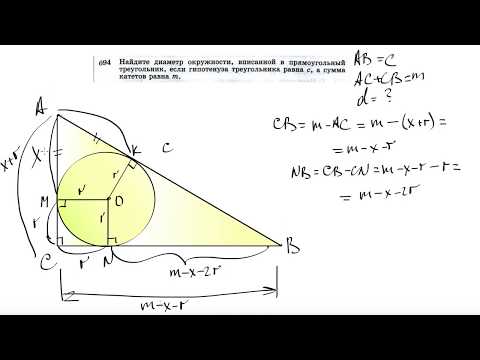
Окружность, вписанная в прямоугольный треугольник, делит гипотенузу на отрезки , равные 5 см и 12см ?

Окружность, вписанная в прямоугольный треугольник, делит гипотенузу на отрезки , равные 5 см и 12см .

Видео:Прямоугольный треугольник. ОкружностьСкачать

Точка касания вписанной окружности делит гипотенузупрямоугольного треугольника на отрезки 4 см и 6 см?

Точка касания вписанной окружности делит гипотенузу

прямоугольного треугольника на отрезки 4 см и 6 см.

Найдите радиусы описаной и вписаной окружности.

Видео:Волшебная формула для вписанной окружностиСкачать

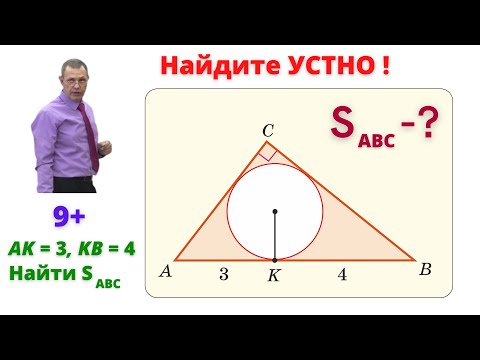
Найти длину высоты прямоугольного треугольника, если эта высота делит гипотенузу на отрезки, длины которых равны 4 и 9?

Найти длину высоты прямоугольного треугольника, если эта высота делит гипотенузу на отрезки, длины которых равны 4 и 9.

Видео:Окружность, вписанная в прямоугольный треугольник | Геометрия 8-9 классыСкачать

Гипотенуза прямоугольного треугольника равна 17, а радиус вписанной окружности этого треугольника равен 3?

Гипотенуза прямоугольного треугольника равна 17, а радиус вписанной окружности этого треугольника равен 3.

Найти периметр этого треугольника.

Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 4см и 21см?

В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 4см и 21см.

Найдите радиус окружности если периметр треугольника равен 56см.

Видео:ОГЭ Задание 25 Окружность вписанная в прямоугольный треугольникСкачать

В прямоугольном треугольнике вписана окружность радиусом 2 см?

В прямоугольном треугольнике вписана окружность радиусом 2 см.

Гипотенуза треугольника 10 см.

Найдите площадь и периметр треугольника.

Видео:Геометрия Центр окружности, вписанной в прямоугольный треугольник удален от концов гипотенузы на aСкачать

В прямоугольном треугольнике точка касания вписанной в него окружности и гипотенузы делит гипотенузу на отрезки, длины которых равны 3 и 7?

В прямоугольном треугольнике точка касания вписанной в него окружности и гипотенузы делит гипотенузу на отрезки, длины которых равны 3 и 7.

Найдите площадь треугольника.

Вы зашли на страницу вопроса Докажите, что вписанная в прямоугольный треугольник окружность делит гипотенузу на отрезки, произведение длин которых равно площади этого треугольника?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

Х — меньший катет, тогда 2х это гипотенуза (так как меньший катет лежит напротив угла в 30°) х + 2х = 36 3х = 36 х = 12, значит гипотенуза 24см.

💥 Видео

№705. Около прямоугольного треугольника ABC с прямым углом С описана окружность. Найдите радиусСкачать

Математика за минуту: Объяснение формулы радиуса вписанной окружности в прямоугольный треугольник.Скачать

Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Вписанная и описанная окружность - от bezbotvyСкачать

Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

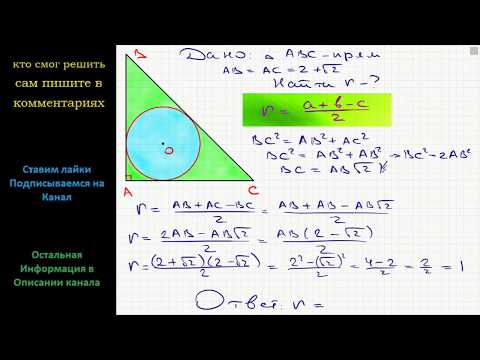
Геометрия Катеты равнобедренного прямоугольного треугольника равны 2+√2. Найдите радиус окружностиСкачать