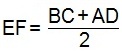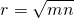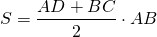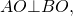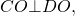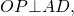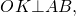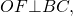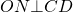В данной статье мы расскажем Вам о свойствах прямоугольной трапеции, как обычной, так и той, в которую вписана окружность.
Для начала напомним некоторые основные определения.
Трапеция – это четырехугольник, имеющий 2 параллельные друг другу стороны, причем 2 другие стороны параллельными не являются.
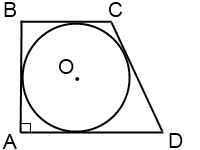
Прямоугольная трапеция — это такая трапеция, одна из боковых сторон которой перпендикулярна ее основаниям (изображена на рис.).
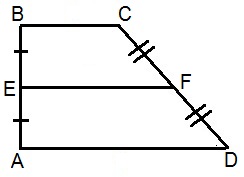
Средняя линия трапеции – это отрезок, который соединяет середины боковых сторон фигуры (на рис. EF).
Видео:СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ #математика #егэ #shorts #профильныйегэСкачать

Основные свойства прямоугольной трапеции
- Средняя линия EF равна половине суммы ее оснований BC и AD.
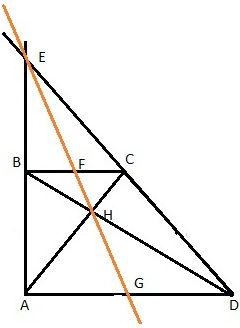
- точка пересечения (H) диагоналей прямоугольной трапеции AC и BD;
- точка пересечения (E) продолжений боковых сторон трапеции AB и CD;
- середины (F и G) оснований трапеции BC и AD.
Данным свойством обладает как прямоугольная, так и равносторонняя трапеция.
Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Свойства прямоугольной трапеции, в которую вписана окружность
SABCD = BC * AD
Узнать подробнее о свойствах трапеции с прямым углом, в которую вписана окружность, а также ознакомиться с доказательствами этих свойств, можно на сайте uznateshe.ru.
Понравилась статья, расскажите о ней друзьям:
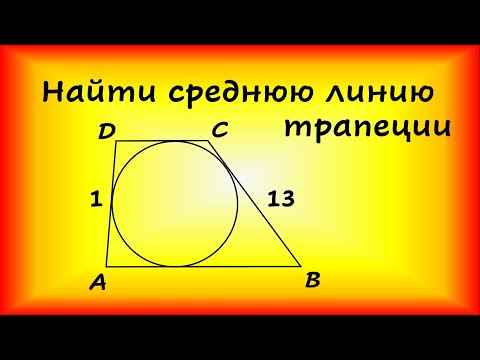
Видео:Боковые стороны трапеции, описанной около окружности, равны 13 и 1. Найдите среднюю линию трапеции.Скачать
Узнать ещё
Знание — сила. Познавательная информация
Видео:8 класс, 49 урок, Средняя линия трапецииСкачать

В прямоугольную трапецию вписана окружность
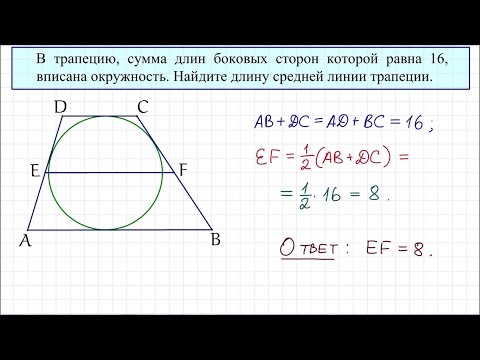
Если в условии задачи сказано, что в прямоугольную трапецию вписана окружность, можно использовать следующие свойства.
1. Сумма оснований трапеции равна сумме боковых сторон.
2. Расстояния от вершины трапеции до точек касания вписанной окружности равны.
3. Высота прямоугольной трапеции равна ее меньшей боковой стороне и равна диаметру вписанной окружности.
4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции.
5. Если точка касания делит боковую сторону на отрезки m и n, то радиус вписанной окружности равен
И еще два полезных свойства прямоугольной трапеции, в которую вписана окружность:
1) Четырехугольник, образованный центром вписанной окружности, точками касания и вершиной трапеции — квадрат, сторона которого равна радиусу. (AMOE и BKOM — квадраты со стороной r).
2) Если в прямоугольную трапецию вписана окружность, площадь трапеции равна произведению ее оснований.
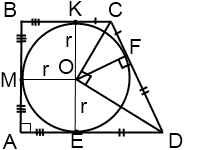
Обозначим CF=m, FD=n. Поскольку расстояния от вершин до точек касания равны, высота трапеции равна двум радиусам вписанной окружности, а
Видео:ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Вписанная в трапецию окружность
Когда в трапецию можно вписать окружность? Какими свойствами обладает вписанная в трапецию окружность? Где находится центр этой окружности? Чему равен ее радиус?
1. В трапецию можно вписать окружность тогда и только тогда когда суммы ее противоположных сторон равны.

2) Обратно, если AD+BC=AB+CD, то в трапецию ABCD можно вписать окружность.
2. Центр вписанной в трапецию окружности — точка пересечения её биссектрис.
O — точка пересечения
биссектрис трапеции ABCD.
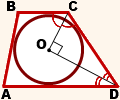
и точка O лежит на средней линии трапеции.



📺 Видео
Трапеция, решение задач. Вебинар | МатематикаСкачать

СРЕДНЯЯ ЛИНИЯ. ТРАПЕЦИЯ. ВПИСАННЫЕ И ОПИСАННЫЕ ЧЕТЫРЕХУГОЛЬНИКИ. Контрольная № 2 Геометрия 8 классСкачать

Трапеция и вписанная окружностьСкачать

Трапеция. Средняя линия трапеции.Скачать
ЕГЭ ВПИСАННАЯ ОКРУЖНОСТЬ В ПРЯМОУГОЛЬНУЮ ТРАПЕЦИЮ | ЗАДНИЙ ХОД В МАТЕМАТИКЕ ИЛИ КАКОЙ ТО ПОДВОХ |Скачать

Геометрия В прямоугольную трапецию вписана окружность радиуса 12 см Большая из боковых сторон точкойСкачать

ВСЕ О СЕЧЕНИЯХ В СТЕРЕОМЕТРИИСкачать

1742. Названия основных геометрических фигур на иврите: мэшулаш, рибУа, мэруба, мэуйан, кадурСкачать

Средняя линия описанной трапеции. ВЫ ТОЧНО ПОПАЛИ!Скачать
Теорема о средней линии трапецииСкачать

Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

88. Средняя линия трапецииСкачать

В равнобедренную трапецию вписана окружность, средняя линия трапеции 3, диагональ 5. Найти высоту трСкачать

Задание 24 ОГЭ по математике #4Скачать