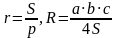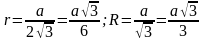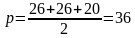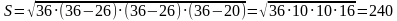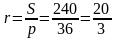Вписанная и описанная окружность в треугольник задачи 9 класс

Урок №7. СКАЧИВАЙТЕ файл на устройства, чтобы все знаки и формулы были видны и распознаны. Во время чтения файла онлайн происходит потеря формул.

Просмотр содержимого документа
«Решение задач по теме «Вписанная и описанная окружности»»

Тема: Решение задач по теме «Вписанная и описанная окружности»

Задачи: продолжить формирование навыков решения задач по теме.

Центр вписанной в треугольник окружности находится в точке пересечения его биссектрис.

Центр описанной около треугольника окружности находится в точке пересечения серединных перпендикуляров.

Формулы нахождения радиуса вписанной r и описанной R около треугольника окружностей.

Для любого треугольника:

Для равностороннего треугольника.

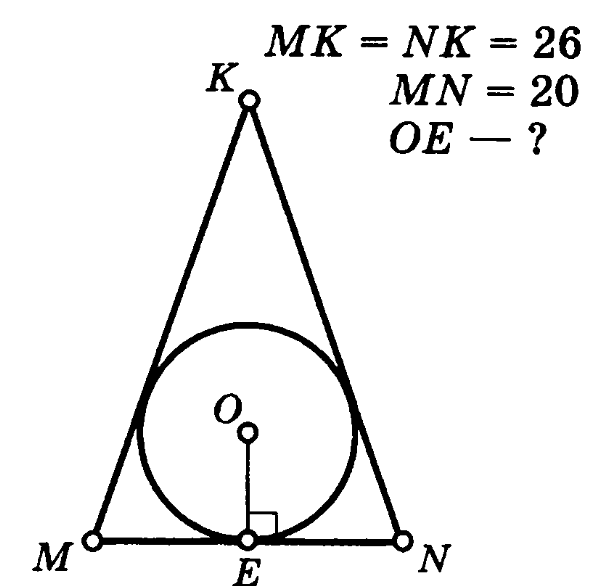
Задача 1. В равнобедренном треугольнике MKN боковые стороны равны 26, а основание – 20. В треугольник вписана окружность с радиусом ОЕ. Найти длину ОЕ.

Решение (краткое). Радиус окружности, вписанной в равнобедренный треугольник можно вычислить по стандартной формуле 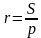, где р – полупериметр.

Ответ: .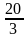

Задача 2. Прямоугольный треугольник KMN описан около окружности радиуса 13. Один из катетов треугольника равен 24. Найти периметр треугольника.

Решение (краткое). MN=d=2r=26, по теореме Пифагора KN=10, Р=60.

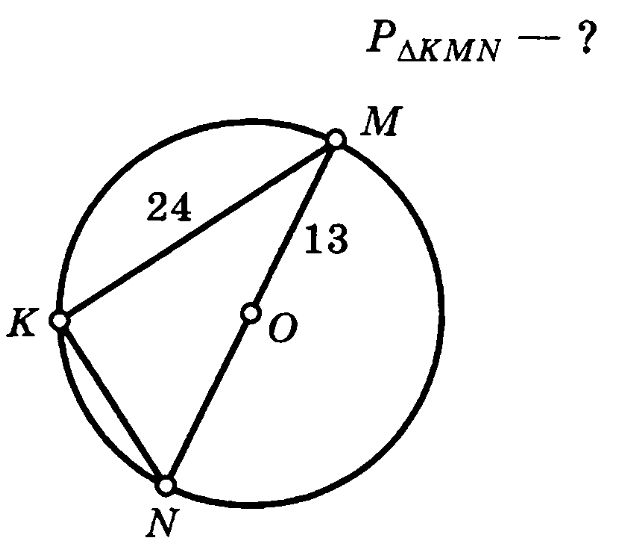
Задача 3. Равнобедренный треугольник АВС вписан в окружность, отрезок ОD=4. Найти площадь треугольника.

Решение (краткое). ОВ=5, ОС=ОВ=5, СD=9, S=0.5*9*6=27.

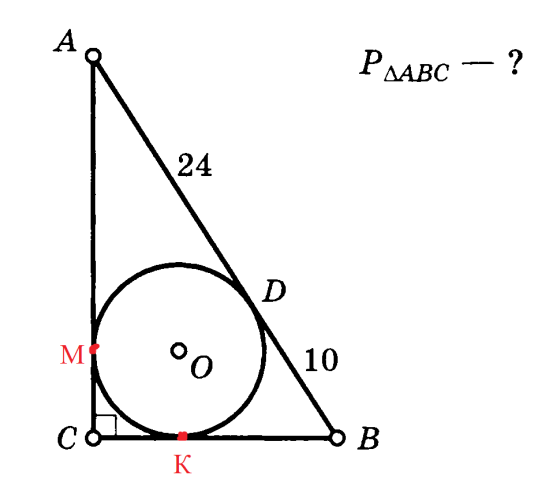
Задача 4. Прямоугольный треугольник описан около окружности. Точка D делит гипотенузу на две части, длинами по 10 и 24. Найти периметр треугольника.

Решение (краткое). DB=DK=10, AD=AM=24.

KOMC – квадрат, т.к. ОК перпендикулярен СВ, ОМ перпендикулярен АС и KC=CM, OK=OM=r.

Пусть KC=CM=х, тогда ВС=10+х, АС=24+х, АВ=24+10=34.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Набор задач на вписанную и описанную окружность при подготовке к ОГЭ ( раздел геометрия)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Задачи на вписанную и описанную окружность при подготовке к ОГЭ.

Окружность с центром в точке О описана около равнобедренного треугольника АВС, в котором АВ=ВС и угол АВС = 28 0 . Найдите величину угла ВОС. Ответ дайте в градусах.

Угол между стороной правильного n -угольника, вписанного в окружность , и радиусом этой окружности, проведённым в одну из вершин стороны, равен 75 0 . Найдите n .

АС и BD -диаметры окружности с центром О. Угол АСВ равен 69 0 . Найдите угол АО D . Ответ дайте в градусах.

Два угла вписанного в окружность четырёхугольника равны 21 0 и 43 0 . Найдите больший из оставшихся углов. Ответ дайте в градусах.

Четырёхугольник АВС D вписан в окружность. Угол АВС равен 128 0 , угол CAD равен 78 0 . Найдите угол ABD . Ответ дайте в градусах.

Стороны четырёхугольника АВС D AB , BC , CD и AD стягивают дуги описанной окружности , градусные величины которых равны соответственно 63 0 , 62 0 , 90 0 , 145 0 . Найдите угол В этого четырёхугольника. Ответ дайте в градусах.

Угол А четырёхугольника АВС D , вписанного в окружность , равен 92 0 . Найдите угол С этого четырёхугольника. Ответ дайте в градусах.

Угол С треугольника АВС, вписанного в окружность радиуса 12, равен 30 0 . Найдите сторону АВ этого треугольника.

Сторона АВ треугольника АВС равна11. Противолежащий её угол С равен 30 0 . Найдите радиус окружности, описанной около этого треугольника.

Около окружности, радиус которой равен 16 , описан квадрат. Найдите радиус окружности, описанного около этого квадрата.

Периметр четырёхугольника , описанного около окружности . равен 56, две его стороны равен 17 и 22. найдите большую из оставшихся сторон.

В четырёхугольник АВС D вписана окружность , АВ =49, CD = 47. Найдите периметр четырёхугольника.

Около окружности описана трапеция, периметр которой равен 120. Найдите её среднюю линию.

около трапеции описана окружность. Периметр трапеции равен 96, средняя линия равна 16. Найдите боковую сторону трапеции.

Сторона ромба равна 34 , острый угол равен 60 0 . Найдите радиус вписанной в этот ромб окружности.

Найдите диагональ прямоугольника, вписанного в окружность , радиус которой равен 40.

Окружность , вписанная в равнобедренный треугольник , делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 25 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

Боковые стороны равнобедренного треугольника равны 5, основание равно 6. найдите радиус окружности, описанной около этого треугольника.

В треугольнике АВС ВС=, угол С равен 90 0 . Радиус окружности, описанной около этого треугольника, равен 8,5. Найдите АС.

Сторона правильного треугольника равна 36. Найдите радиус окружности , описанной около этого треугольника.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 988 человек из 78 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 310 человек из 68 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 673 человека из 75 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 536 528 материалов в базе

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 30.06.2017
• 1034
• 13

• 30.06.2017
• 2151
• 0

• 30.06.2017
• 392
• 0

• 30.06.2017
• 2215
• 10

• 30.06.2017
• 679
• 0

• 30.06.2017
• 432
• 3

• 30.06.2017
• 253
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 30.06.2017 9060
• DOCX 15.1 кбайт
• 323 скачивания
• Рейтинг: 3 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Коровятская Наталья Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 4 месяца
• Подписчики: 0
• Всего просмотров: 14686
• Всего материалов: 7

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид

Время чтения: 1 минута

В Омской области школы и колледжи перейдут на дистанционное обучение с 7 по 21 февраля

Время чтения: 1 минута

Минтруд рекомендовал перевести на удаленку максимальное число сотрудников

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Путин поручил обучать педагогов работе с девиантным поведением

Время чтения: 1 минута

В ЕГЭ обновили задания по математике

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Вписанные и описанные окружности. Геометрия 9 класс. Ключевая задача № 3.Скачать

Вписанная и описанная окружность в треугольник задачи 9 класс

Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.

Воспользуемся теоремой косинусов:

(здесь a и b — боковые стороны равнобедренного треугольника, c — основание.

Диаметр описанной окружности найдем по обобщенной теореме синусов:

Вместо того, чтобы искать основание треугольника, можно было найти угол при основании. Действительно, сумма углов при основании данного равнобедренного треугольника равна 60°. Эти углы равны, поэтому каждый из них равен 30°. Применяя обобщенную теорему синусов для боковой стороны и противолежащего ей угла, получаем:

Приведем решение Андрея Ларионова.

Угол при основании равен

Следовательно, дуга описанной окружности, на которую он опирается, равна 2 · 30° = 60°. Эту дугу стягивает боковая сторона треугольника.

Хорда, стягивающая дугу в 60°, равна радиусу окружности, поэтому радиус описанной окружности равен боковой стороне треугольника, тогда D = 2 · 4 = 8.

🔥 Видео

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Геометрия 9 класс. Вписанные и описанные окружности. Ключевая задача № 4.Скачать

Вписанная и описанная окружности. ЗадачиСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Вписанные и описанные окружности. Геометрия 9 класс. Ключевая задача №2.Скачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Вписанные и описанные окружности. С. р. 3 в1 9 классСкачать

Тема 7. Вписанные и описанные окружности треугольникаСкачать

Геометрия 9 класс : Окружность. Описанная и вписаннаяСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Геометрия. 9 класс. Формулы для нахождения радиусов вписанной и описанной окружностей треугольникаСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Формулы для радиусов вписанной и описанной окружностей треугольника Геометрия 9классСкачать

Углы, вписанные в окружность. 9 класс.Скачать