Вокруг окружности описали квадрат площадь которого равна 64 найдите радиус

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около квадрата. Также разберем примеры решения задач для закрепления изложенного материала.

Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Формулы вычисления радиуса описанной окружности

Через сторону квадрата

Радиус R окружности, описанной около квадрата, равняется длине его стороны a, умноженной на квадратный корень из двух и деленной на два.

Через диагональ квадрата

Радиус R описанной вокруг квадрата окружности равен половине его диагонали d.

Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Примеры задач

Задание 1

Длина стороны квадрата равняется 8 см. Найдите радиус описанной вокруг него окружности.

Применим первую формулу, рассмотренную выше:

Задание 2

Вычислите длину диагонали квадрата, если радиус описанной вокруг него окружности составляет 6 см.

Как мы знаем, радиус описанной окружности равняется половине диагонали квадрата. Следовательно, общая длина диагонали равняется 12 см (6 см ⋅ 2).

Видео:Найти площадь квадрата описанного около окружности радиуса 19Скачать

Квадрат. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):

Можно дать и другие определение квадрата.

Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.

Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).

Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Свойства квадрата

• Длины всех сторон квадрата равны.
• Все углы квадрата прямые.
• Диагонали квадрата равны.
• Диагонали пересекаются под прямым углом.
• Диагонали квадрата являются биссектрисами углов.
• Диагонали квадрата точкой пересечения делятся пополам.

Изложеннные свойства изображены на рисунках ниже:

Видео:15 задание треугольники огэ по математике / маттаймСкачать

Диагональ квадрата

Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

(1)

Из равенства (1) найдем d:

.

(2)

Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.

Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:

Ответ:

Видео:Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.Скачать

Окружность, вписанная в квадрат

Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):

Видео:Длина окружности. Математика 6 класс.Скачать

Формула вычисления радиуса вписанной окружности через сторону квадрата

Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:

(3)

Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.

Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:

Ответ:

Видео:Задание 16 ОГЭ по математике. Окружность описана около квадратаСкачать

Формула вычисления сторон квадрата через радиус вписанной окружности

Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:

(4)

Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.

Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:

Ответ:

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Окружность, описанная около квадрата

Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

(5)

Из формулы (5) найдем R:

(6)

или, умножая числитель и знаменатель на , получим:

.

(7)

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Формула стороны квадрата через радиус описанной около квадрата окружности

Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.

Из формулы (1) выразим a через R:

.

(8)

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать

Периметр квадрата

Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

(9)

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:

Ответ:

Видео:Площадь круга. Математика 6 класс.Скачать

Признаки квадрата

Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.

Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).

Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть

(10)

Так как AD и BC перпендикулярны, то

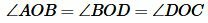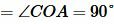(11)

Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда

(12)

Эти реугольники также равнобедренные. Тогда

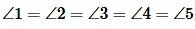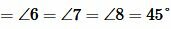(13)

Из (13) следует, что

(14)

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Найдите площадь квадрата описанного вокруг окружности радиуса 64?

Математика | 5 — 9 классы

Найдите площадь квадрата описанного вокруг окружности радиуса 64.

Можно попробовать провести диаметр через цент окружности, параллельный одной из сторон квадрата.

Получается, что мы находим саму сторону :

Площадь квадрата находиться по формуле :

S = a2(a в квадрате)

S = 128 * 128 = 16384.

Видео:2134 около окружности радиус которой равен 16 корней из 2Скачать

Докажите, что отношение площади квадрата, вписанного в окружность, до площади квадрата, описанного вокруг окружности, равна 1 : 2?

Докажите, что отношение площади квадрата, вписанного в окружность, до площади квадрата, описанного вокруг окружности, равна 1 : 2.

Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

Около окружности, радиус которой равен корень 8, описан квадрат?

Около окружности, радиус которой равен корень 8, описан квадрат.

Найдите радиус окружности, описанной около этого квадрата.

Видео:Радиус описанной окружностиСкачать

Найдите площадь квадрата , описанного вокруг окружности радиуса 7?

Найдите площадь квадрата , описанного вокруг окружности радиуса 7.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Найдите площадь квадрата, описанного вокруг окружности радиуса 84?

Найдите площадь квадрата, описанного вокруг окружности радиуса 84.

Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Найти площадь квадрата описанного около окружности радиуса 25?

Найти площадь квадрата описанного около окружности радиуса 25.

Видео:ОГЭ ЗАДАНИЕ 16 #математика #2023 #огэ #math #огэпоматематикеСкачать

Найдите площадь квадрата описанного около окружности радиуса 4?

Найдите площадь квадрата описанного около окружности радиуса 4.

Найдите площадь куадрата, описанного вокруг окружности радиуса 83?

Найдите площадь куадрата, описанного вокруг окружности радиуса 83.

Вокруг окружности описаны квадрат и правильный шестиугольник?

Вокруг окружности описаны квадрат и правильный шестиугольник.

Найдите отношение площадей этих фигур.

Найдите площадь кольца между вписанной и описанной вокруг квадрата окружностями, если его сторона 1 / корень из пи?

Найдите площадь кольца между вписанной и описанной вокруг квадрата окружностями, если его сторона 1 / корень из пи.

Найдите площадь квадрата, описанного около окружности радиуса 32?

Найдите площадь квадрата, описанного около окружности радиуса 32.

На этой странице находится ответ на вопрос Найдите площадь квадрата описанного вокруг окружности радиуса 64?, из категории Математика, соответствующий программе для 5 — 9 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Математика. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

Найдём скорость 2 машины : 74 — 12 = 62. Скорость с которой машины отдаляются друг от друга : 62км / ч + 74км / ч = 136км / ч. А в условии 6 часов, значит через 6 часов перед ними будет 136х6 = 816км. Ответ : 816км будет между этими машинами через..

20 5 = 4 . 4х2 = 8 . 8 20 (сьедино) = Ответ 2 5.

А) навстречу т. К. 400 — 60 * 2 + 90 * 2 = 400 — 120 — 180 = 100 км б) противоположно, в) автобус противоположно, а автомобиль в сторону автобуса, 400 — 180 + 120 = 340 км г) автомобиль противоположно, а автобус в сторону автомобиля, 400 + 180 — 120..

Приложение Photomath скачай.

(( — 1) ^ 4) / 4 — (( — 1) ^ 3) / 3 — 1 = 1 / 4 — 1 / 3 — 1 = — 13 / 12.

Разрезать пополам — 2 по 8 ещё пополам — 4 по 4 ещё раз — 8 по 2 ещё — 16 по 1.

Че­ловек стал пря­мохо­дящим из — за оби­лия в Вос­точной и Юж­ной Аф­ри­ке гор — та­кой лан­дшафт в этом ре­ги­оне сфор­ми­ровал­ся в эпо­ху пли­оце­на бла­года­ря вул­ка­ничес­кой ак­тивнос­ти и сме­щению тек­то­ничес­ких плит. Го­мини­ды, на­ши п..

Потому что это было наиболее выгодно с точки зрения эволюции, ибо когда ты выше, можно заметить врага на большем расстоянии. В дикие времена было полезно.

1, 8х + 4, 6х — 0, 6 = 1 6, 4х — 0, 6 = 1 6, 4х = 1 + 0, 6 6, 4х = 1, 6 х = 1, 6 : 6, 4 х = 1 : 4 х = 0, 25.

40 : 2 = 20 промежутков по 3 минуты 20 * 3 = 60 минут потрачено на чтение Перерывов на 1 меньше, т. Е. 19. 19 * 2 = 38 минут — перерыв. 60 + 38 = 98 минут затрачено на чтение всей книги.