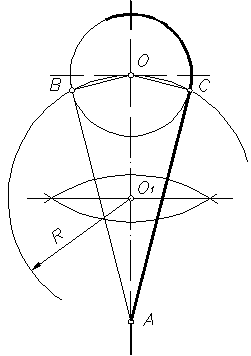
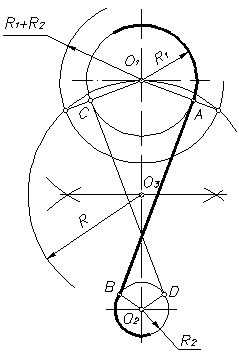
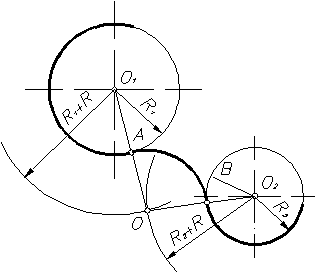Общие касательные к двум окружностям
 Взаимное расположение двух окружностей Взаимное расположение двух окружностей |
 Общие касательные к двум окружностям Общие касательные к двум окружностям |
 Формулы для длин общих касательных и общей хорды Формулы для длин общих касательных и общей хорды |
 Доказательства формул для длин общих касательных и общей хорды Доказательства формул для длин общих касательных и общей хорды |
Видео:Внешняя касательная к двум окружностямСкачать
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
 | ||
| Внешнее касание двух окружностей | ||
 | ||
| Внутреннее касание двух окружностей | ||
 | ||
| Окружности пересекаются в двух точках | ||
 | ||
 | ||
| Каждая из окружностей лежит вне другой | ||
 Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
 Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
 Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
 | |
| Внутреннее касание двух окружностей | |
 | |
| Окружности пересекаются в двух точках | |
 | |
| Внешнее касание двух окружностей | |
 | |
 | |
| Каждая из окружностей лежит вне другой | |
 | |
| Внешняя касательная к двум окружностям | |||||||||||||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||||||||||||
| Внутреннее касание двух окружностей | |||||||||||||||||||||
| Окружности пересекаются в двух точках | |||||||||||||||||||||
| Внешнее касание двух окружностей | |||||||||||||||||||||
| Каждая из окружностей лежит вне другой | |||||||||||||||||||||
| Фигура | Рисунок | Формула | ||||||||||||
| Внешняя касательная к двум окружностям |  | |||||||||||||
| Внутренняя касательная к двум окружностям |  | |||||||||||||
| Общая хорда двух пересекающихся окружностей |  | |||||||||||||
| Внешняя касательная к двум окружностям | ||||
 | ||||
| Внутренняя касательная к двум окружностям | ||||
 | ||||
| Общая хорда двух пересекающихся окружностей | ||||
 | ||||
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
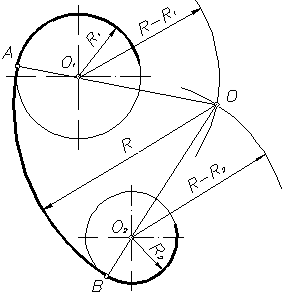
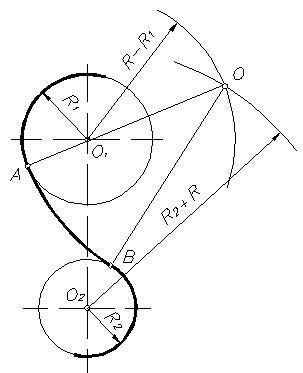
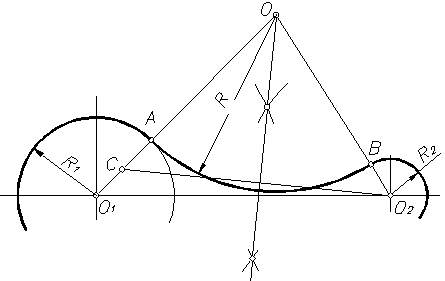
 Длина общей хорды двух окружностей вычисляется по формуле Видео:Внутренняя касательная к двум окружностямСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Касательные к окружностиСкачать  Построение общей внутренней касательной к двум окружностямДаны две окружности (а это значит, что даны и их центры O1 и O2). Требуется провести общую внутреннюю касательную к ним, то есть такую касательную, от которой данные окружности лежат по разные стороны. Радиус большей окружности называем R, радиус меньшей окружности — r. Сначала вокруг меньшей окружности построим вспомогательную окружность с тем же центром и с радиусом, равным сумме радиусов двух данных окружностей (R + r). Затем построим из центра большей окружности вспомогательную касательную к вспомогательной окружности. Требуемая внутренняя касательная будет параллельна вспомогательной касательной. Отложим первый вспомогательный луч с началом в точке A. Замерим циркулем радиус большей окружности, и тем же раствором циркуля от начала первого луча отложим отрезок AB, равный R. Теперь циркулем замерим радиус меньшей окружности, и тем же раствором циркуля от точки B отложим отрезок BC, равный r. Получился отрезок AC, равный сумме радиусов двух данных окружностей (R + r). Замерим AC циркулем, и тем же раствором циркуля построим первую вспомогательную окружность с центром в O1. Теперь соединим отрезком центры O1 и O2. Произвольным раствором циркуля строим вторую вспомогательную дугу окружности с центром O1. И тем же раствором циркуля строим третью вспомогательную дугу окружности с центром O2 — так, чтобы третья дуга пересекала вторую в двух точках (называем их D и E). Соединяем D и E отрезком, который пересекает O1O2 в середине — эту точку называем F. Теперь замерим циркулем FO1 и этим раствором циркуля строим четвёртую вспомогательную окружность с центром в F на отрезке O1O2, как на диаметре. Эта четвёртая окружность пересекает первую вспомогательную окружность в двух точках (называем их G и H). Выбираем из этих двух точек ту, которая нам больше нравится (в данном построении это точка H), и соединяем прямой с точкой O2. Прямая HO2 — это касательная к первой вспомогательной окружности, проходящая через центр большой данной окружности. Прямая HO2 пересекла большую окружность в двух точках (называем их K и L). Эти точки равно отстоят от O2 и помогут нам построить перпендикуляр к HO2. Произвольным раствором циркуля проводим пятую вспомогательную дугу окружности с центром в K. Тем же раствором циркуля проводим шестую вспомогательную дугу окружности с центром в L — так, чтоб шестая дуга пересекала пятую в некоторой точке (называем точку M). Соединяем O2 и M прямой — эта прямая (перпендикуляр к HO2) пересекает большую данную окружность в некоторой точке (называем её N). Теперь через N проведём прямую, параллельную вспомогательной касательной HO2. Произвольным раствором циркуля строим седьмую вспомогательную окружность с центром в точке N — так, чтоб седьмая окружность пересекала HO2 в двух точках (точки называем P и Q). Тем же раствором циркуля строим восьмую вспомогательную окружность с центром в Q, и восьмая окружность пересекает вспомогательную касательную HO2 в двух точках (точки называем Z и S). Тем же раствором циркуля проводим девятую вспомогательную дугу окружности с центром в S — так, чтобы девятая дуга пересекала седьмую окружность в некоторой точке (точку называем T). Соединяем N и Т прямой — эта прямая NT и будет требуемой общей внутренней касательной к двум данным окружностям. И вот почему. NT проходит через конец радиуса O2N, лежащий на окружности. Также по построению NT параллельна HO2 и перпендикулярна радиусу O2N — следовательно, NT — касательная к большой данной окружности. Теперь проведём радиус O1H и точку его пересечения с прямой TN называем U. Радиус O1H перпендикулярен касательной O2H — значит, угол O2HU — прямой. Получилось, что в четырёхугольнике UHO2N есть три прямых угла — значит, и четвёртый угол HUN прямой, и UHO2N — прямоугольник, в котором сторона HU равна противоположной стороне O2N, то есть радиусу R. Теперь можем найти длину отрезка O1U (составляющего вместе с UH отрезок O1H). Длина равна разности длин O1H и HU, то есть (r + R) — R = r. Выходит, что U отстоит от O1 на r, то есть U лежит на меньшей данной окружности, а это значит, что TN, проходящая через U — проходит через конец радиуса O1U, лежащий на окружности, и перпендикулярна радиусу, то есть TN — касательная к меньшей данной окружности. Построение закончено. Видео:Построение касательной двум окружностям внешнего касанияСкачать  СОПРЯЖЕНИЕ ДВУХ ОКРУЖНОСТЕЙВозможны два варианта построений сопряжений двух окружностей: · Задан радиус сопряжения. · Задана точка сопряжения на одной из окружностей. Сопряжение может быть внешним, внутренним и смешанным. 1. Сопряжение двух окружностей дугой заданного радиуса R (Рисунок16) При внешнем сопряжении (рисунок 16) центр сопряжения О определяется пересечением двух геометрических мест – вспомогательных окружностей радиусов R1 + R и R2 + R, проведенных соответственно из центров сопрягаемых дуг, то есть из точек О1 и О2. Точки сопряжения А и В определяются как точки пересечения заданных дуг с прямыми ОО1 и ОО2. При внутреннем сопряжении (рисунок 17) центр сопряжения О определяется пересечением двух геометрических мест – вспомогательных окружностей радиусов R – R1 и R – R2, проведенных соответственно из О1 и О2 (рисунок 17). При смешанном сопряжении (рисунок 18) центр сопряжения О определяется в пересечении вспомогательных окружностей радиусов R — R1 и R + R2, проведенных соответственно из О1 и О2. Точки сопряжения А и В лежат на пересечении линий центров ОО1 и ОО2 с дугами заданных окружностей. 2. Сопряжение двух окружностей, если задано точка сопряжения А на одной из окружностей (рисунок 19). Соединяют точку А с центром О1 и откладывают на этой прямой отрезок АС, равный R2. К середине отрезка СО2 восставляют перпендикуляр до пересечения с продолжением линии О1А. Точка О пересечения и является центром сопряжения. Вторая точка сопряжения В лежит на пересечении линии центров ОО2 с дугой второй окружности. Рисунок 19 ПОСТРОЕНИЕ КАСАТЕЛЬНЫХ Построение касательных к окружности основано на том, что касательная перпендикулярна к радиусу, проведенному в точку касания. 1. Касательная к окружности из точки А, лежащей вне окружности (рисунок 20). Отрезок ОА, соединяющий данную точку с центром окружности, делят пополам и из полученной О1, как из центра описывают вспомогательную окружность радиусом R = О1А. Вспомогательная окружность пересекает заданную в точке С. Прямая АС является касательной к окружности, так как угол АСО прямой, как вписанный в окружность и опирающийся на ее диаметр. 2. Касательная к двум окружностям может быть внешней, если обе окружности расположены с одной стороны от нее, и внутренней, если окружности расположены с разных сторон от касательных. 2.1 Внешняя касательная к окружностям радиусов R1 и R2 (рисунок 21). Из центра О1 большей окружности проводят вспомогательную окружность радиусом R1 – R2. Отрезок О1О2 делят пополам и проводят вспомогательную окружность радиусом R = О3О1. Точки пересечения этих окружностей соединяют с центром О1 и продолжают до пересечения с окружностью радиуса R1 в точках В и D. Эти точки являются точками касания окружности большего диаметра. Из центра О2 проводят прямые О2А и О2С, соответственно параллельные О1В и ОD, до пересечения с контуром окружности в точках А и С. Прямые АВ и СD – искомые внешние касательные к двум окружностям. 2.2 Внутренняя касательная к двум окружностям радиусов R1 и R2 (рисунок 22). Рисунок 22 Из центра окружности О1 проводят вспомогательную окружность радиусом R1 + R2. Делят отрезок О1О2 пополам, и из полученной точки О3 проводят вторую вспомогательную окружность радиусом R = О3О1. Точки пересечения этих окружностей соединяют с центром О1 и на пересечении с окружностью радиуса R1 получают точки касания А и С. Из точки О2 проводят прямую, параллельную прямой О1А, и получают точку касания В на малой окружности. Аналогично построена точка касания D. Прямые АВ и СD – искомые внутренние касательные к двум окружностям. 🔥 ВидеоПостроение общей внутренней касательной к двум окружностямСкачать  Построение внешней касательной к двум дугам окружностей. Урок11.(Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать  Построение общей внешней касательной к двум окружностямСкачать  1 2 4 сопряжение окружностейСкачать  Касательные к двум окружностям.Скачать  Построение касательной к окружностиСкачать  Построение общей касательной к двум окружностямСкачать  Построение касательной к окружности.Скачать  Построение общей касательной к двум окружностямСкачать  Черчение. Внутреннее, внешнее и смешенное сопряжение двух окружностей.Скачать  Построение касательной к окружностиСкачать  Построение общей касательной к двум окружностямСкачать  Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  Внутреннее сопряжение двух дуг окружностей третьей дугой. Урок14.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать  Внешнее сопряжение двух дуг окружностей третьей дугой. Урок13.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать  |