Как строить фигуры треугольников

Видео:Геометрические фигуры на HTML и CSS // Треугольник стрелка круг трапеция и другиеСкачать

Задачи на построение

Широкое распространение в геометрии получили задачи на построение. Суть этих задач состоит в следующем: при заданных начальных условиях нужно построить тот или иной геометрический объект при помощи линейки и циркуля. Разберем общие принципы решения данных задач:

Анализирование задачи. На этом этапе необходимо установить взаимосвязь между заданными условиями и объектом, который нужно изобразить. Результатом выполнения этого этапа является план решения задачи.

Построение. Согласно разработанного плана выполняется построение объекта.

Доказательство. На этом этапе необходимо доказать, что изображенная фигура полностью соответствует заданным условиям.

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

Изучение. На этом этапе выполняется анализ начальных условий и определение, при каких условиях задача решается одним способом, при каких двумя, а при каких – вовсе не решаема.

Разберем задачи на построение треугольника по трем различным начальным условиям.

Видео:Осевая симметрия, как начертить треугольники симметричноСкачать

Изображение треугольника, если задана одна сторона и два прилегающих к ней угла

Задана одна сторон треугольника (BC) и прилежащие к ней углы (∝) и (β) , необходимо построить треугольник.

1. Анализируем условия. Необходимо построить треугольник (ABC) , имея одну сторону (BC) и углы (∠K= ∝ и ∠M= β) к ней прилежащие. Разработаем план решения задачи:

• Начертим прямую a, а на ней отмерим отрезок (BC) ;
• Изображаем угол (∠K= ∝) с центром в вершине (B) на стороне (BC) ;
• Изображаем угол (∠M= β) с центром в вершине (C) на стороне (BC) ;
• На пересечении лучей построенных углов получим точку (A) , соединяем ее с точками (C) и (B) , получаем отрезки (AC) и (AB) .

2. Строим треугольник

3. Доказательство. По изображенному рисунку делаем вывод, что все заданные условия выполнены в полной мере.

4. Изучение. Заданные углы могут быть построены и в противоположную сторону, соответственно мы можем построить еще один треугольник, но так как он точно такой же, как и первый, можно считать, что решение этой задачи единственное. Учитывая то, что сумма всех углов треугольника должна равняться 180 0 , если сумма углов (∝) и (β) будет равна или больше 180 0 , решения задача не будет иметь.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Изображение треугольника, если заданы три стороны

Заданы три стороны треугольника (AB) , (AC) и (BC) , нужно построить треугольник.

1. Анализируем условия. Необходимо построить треугольник (ABC) , имея три стороны (AB) , (AC) и BC. Разработаем план решения задачи:

• Начертим прямую (a) , а на ней отмерим отрезок (AB) ;
• Чертим с помощью циркуля две окружности. Одна окружность будет с центром в точке (A) с радиусом (AC) , а вторая с центром в точке (B) с радиусом (BC) ;
• На пересечении окружностей мы получим точку (C) , соединяем ее с точками (A) и (B) , получаем отрезки (AC) и (BC) .

2. Строим треугольник:

3. Доказательство. По изображенному рисунку делаем вывод, что все заданные условия выполнены в полной мере.

Не нашли что искали?

Просто напиши и мы поможем

4. Изучение. Построенные окружности имеют две точки пересечения, поэтому мы можем построить еще один треугольник, но так как он точно такой же, как и первый, можно считать, что решение этой задачи единственное. Учитывая то, что сумма двух сторон треугольника всегда больше, чем третья его сторона, можно сделать вывод, если это условие не будет выполнено для заданных сторон, то задача не будет иметь решение.

Видео:Построение треугольника в трёх проекцияхСкачать

Изображение треугольника, если заданы две стороны и угол между ними

Заданы две стороны треугольника (AB) и (AC) , а также угол ∝ между ними, необходимо построить треугольник.

1. Анализируем условия. Необходимо построить треугольник (ABC) , имея стороны (AB) и (AC) , а также угол (CAB) , равный (∝) . Разработаем план решения задачи:

• начертим прямую (a) , а на ней отмерим отрезок (AB) ;
• отмеряем угол (MAB) , равный (∝) ;
• откладываем отрезок (AC) на прямой (AM) ;
• чертим третью сторону треугольника (CB) , соединяя точки (B) и (C) .

2. Строим треугольник:

3. Доказательство. По изображенному рисунку делаем вывод, что все заданные условия выполнены в полной мере.

4.Изучение. Прямая a бесконечна, поэтому таких треугольников можно изобразить очень много, но учитывая тот факт, что они все одинаковые, будем считать, что задача имеет одно решение. При условии, если угол (∝) будет равен или больше 180 0 , решения задача не будет иметь, так как сумма всех углов треугольника должна равняться 180 0 .

Видео:Как построить точки в системе координат OXYZСкачать

Осевая и центральная симметрия

О чем эта статья:

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

• Ось симметрии угла — биссектриса.
• Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
• Оси симметрии прямоугольника проходят через середины его сторон.
• У ромба две оси симметрии — прямые, содержащие его диагонали.
• У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
• Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Видео:Натюрморт из геометрических предметовСкачать

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

1. Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
2. Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
3. С другой стороны прямой отложим такие же расстояния.
4. Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
5. Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

1. Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
2. Измеряем расстояние от вершин до точек на прямой.
3. Откладываем такие же расстояния на другой стороне оси симметрии.
4. Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

1. Проводим через точку А прямую, перпендикулярную прямой l.
2. Проводим через точку В прямую, перпендикулярную прямой l.
3. Измеряем расстояния от точек А и В до прямой l.
4. Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.
5. Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Видео:Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

1. Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
2. Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
3. Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
4. Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

1. Измеряем расстояние от точки B до точки О и от точки А до точки О.
2. Проводим прямую из точки А через точку О и выводим ее на другую сторону.
3. Проводим прямую из точки B через точку О и выводим ее на другую сторону.
4. Чертим на противоположной стороне отрезки А₁О и B₁О, равные отрезкам АО и АB.
5. Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Видео:САМАЯ ПОПУЛЯРНАЯ ФИГУРА В ТРЕЙДИНГЕ! КАК ТОРГОВАТЬ ПО ТРЕУГОЛЬНИКУ НА OLYMP TRADE!Скачать

Симметричный треугольник

В этой статье разберемся что такое симметричный треугольник. Трейдинг используя симметричный треугольник. Где появляется и что означает.

На эту тему есть видео на нашем канале YouTube — Симметричный треугольник

Последние новости в канале телеграмм — PROТрейдинг
Общение на тему теханализа в чате телегам — PROТрейдинг Chat

Видео:Построить линию пересечения треугольников ABC и DEF. Определить видимость. Вариант 2Скачать

Фигура технического анализа симметричный треугольник

Каждый опытный технический аналитик знает, что в развитии тренда не переменно случаются остановки. В эти остановки образуется фигура технического анализа треугольник. Далее тренд продолжается.

Треугольник фигура технического анализа

В трейдинге есть несколько фигур технического анализа треугольник. В данной статье проведет анализ и разбор фигуры симметричный треугольник.

Что такое фигура симметричный треугольник трейдинг

Взглянем на иллюстрацию, развитие динамики цены вверх, то есть тренд восходящий, в развитии тенденции наметилась пауза, рынок ушел в боковик, с образованием фигуры симметричный треугольник.
После чего цена пробила линию сопротивления и тренд возобновился вверх.
Данное правило справедливо и для нисходящего тренда, например тренд нисходящий, наметился баланс с явным образование фигуры симметричный треугольник, в этом случае при пробитии линии сопротивления тренд продолжится вниз.

Как построить фигуру технического анализа симметричный треугольник

Для того чтобы технический аналитик смог построить фигуру симметричный треугольник, необходимо 4 контрольных точки.
Что это за точки? Это линии тренда, чтобы построить линию тренда необходимо два последовательных спада. Далее делается проекция этой линии тренда через точки последовательный пиков.
Проведя эти линии, мы получаем две линии тренда которые в конце концов сходятся в одном месте образуя треугольник.

Построение фигуры симметричный треугольник

Взглянем на картинку, тренд развивается вверх, рынок восходящий. Далее цена начинается идти в бок, образуются спады и пики. Первым делом проводится нисходящая линия тренда через пик один, и пик три.
Далее по мере развития тенденции проводится восходящая линия тренда через спад два, и спад четыре.
Получаем две линии тренда, которые сходятся вместе и образуют фигуру технического анализа симметричный треугольник.
Теперь когда фигура построена с использованием четырех контрольных точек, технический аналитик, трейдер понимает что на рынке образовалась фигура нисходящий треугольник.

Когда ждать пробоя симметричного треугольника

Как правило импульс на слом фигуры технического анализа симметричный треугольник стоит ожидать ближе к точке схождения двух трендовых линий.

Временной фактор завершения фигуры симметричный треугольник в трейдинге

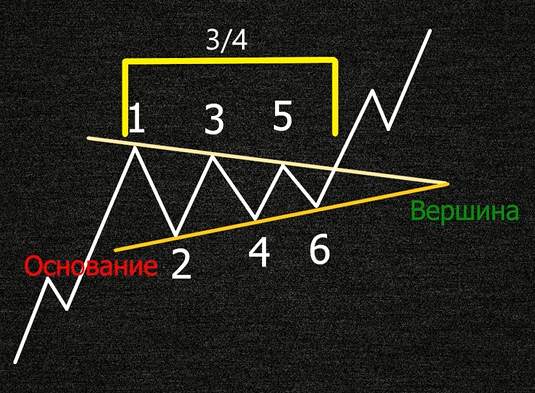
Так же многими техническими аналитиками и опытными трейдерами было замечено, что прорыв происходит не доходя одной четверти фигуры симметричный треугольник.
То есть проводится измерение фигуры, от точки её формирования один, до точки схождения двух трендовых линий. Это расстояние делится на 4, берется 3 части и делается пометка.
Что дает нам это расстояние в три четверти. Это дает понимание когда будет совершен прорыв, и его силу. Импульс происходит от формирования спада под цифрой четыре, до отметки в три четверти.
Чем ближе к трем четвертям тем мощнее. Если цена ушла за отметку три четверти, то сила фигуры симметричный треугольник начинает падает в прогрессии.

Чем же так хорош симметричный треугольник в трейдинге ? Тем что технический аналитик рассматривает его с двух сторон с ценовой стороны и со стороны времени.

Симметричный треугольник и аналитика ложных сигналов

Фигура технического анализа симметричный треугольник может давать ложные сигналы, давай разберем несколько таких ситуаций.

Ложный сигнал фигуры технического анализа симметричный треугольник

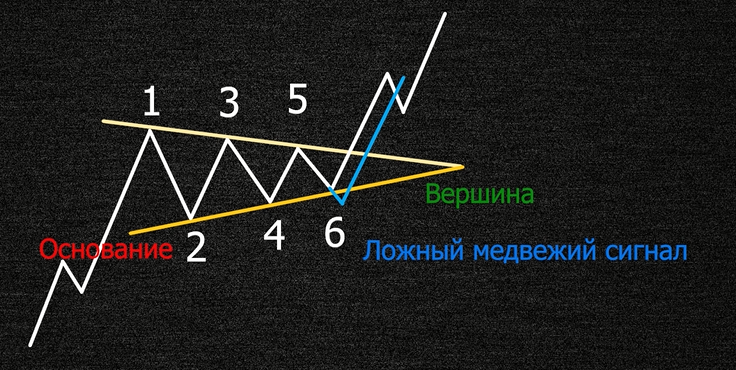
Где возникают ложные сигналы фигуры симметричный треугольник? В большинстве случаев ложные сигналы возникаю в конце образовавшейся фигуры.
На иллюстрации изображен ложный медвежий вынос, цена уходит ниже восходящей трендовой линии, образуя балансовую зону, далее происходит резкий импульс вверх с продолжением основной тенденции.

Значение объема при построении фигуры симметричный треугольник

Рассмотрим иллюстрацию, на рынке восходящий тренд, образовался разворот и консолидация, объем при этом падает, далее проведя линии тренда, технический аналитик понимаем что перед ним симметричный треугольник. Основная особенной фигуры симметричный треугольник в том что объем по мере развития треугольника падает. На прорыве нисходящего тренда объем возрастает.
Выброс объема при пересечении цены восходящей трендовой линии говорит о возможном ложной выносе.

Измерение фигуры симметричный треугольник

Зачем мы проводим измерении фигуры треугольник ? Для того чтобы определить возможные ценовые ориентиры отката цены, так же для фильтрации импульса на возобновлении тренда.
Чтобы измерить фигуру симметричный треугольник есть два варианта.

Первый вариант измерения фигуры технического анализа симметричный треугольник

Рассмотрим рисунок, на нем изображен первый способ измерения симметричного треугольника, от пика А, проведем вниз линию до линии восходящего тренда. Далее проекции этой линии откладываем от прорыва фигуры треугольник.

Второй вариант измерения симметричного треугольника

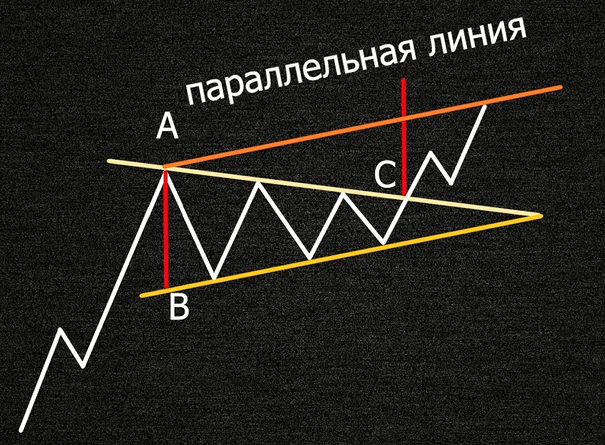
Чтобы выполнить второй вариант измерения, необходимо сделать проекцию восходящей линии тренда, начало проекции начать с первого пика фигуры А.

📺 Видео

Эти ФИГУРЫ Должен Знать Каждый Трейдер! Графические Фигуры И Трейдинг! Теханализ Бинарные Опционы!Скачать

ПАТТЕРН ТРЕУГОЛЬНИК В ТРЕЙДИНГЕ - ВСЯ СУТЬ!Скачать

Типичный урок геометрииСкачать

Как строить простые фигуры в майнкрафтеСкачать

Технический анализ треугольник [Артём Звёздин]Скачать

Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

ВПР 6 класс. 12 задание. Фигура симметиичная данной относительно оси.Скачать

Построение следов плоскостиСкачать

Лайфхак! Площади всех фигур #огэ #математика #shortsСкачать