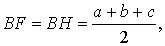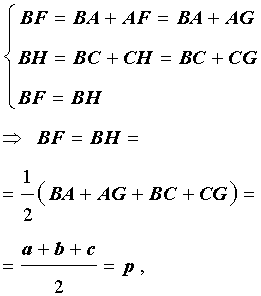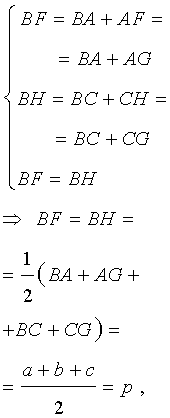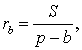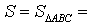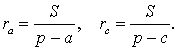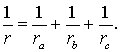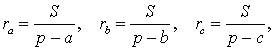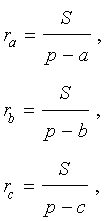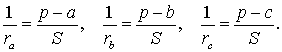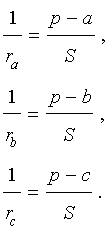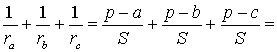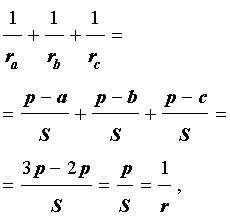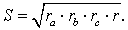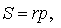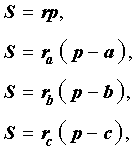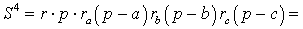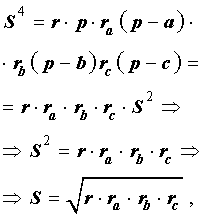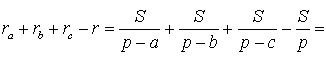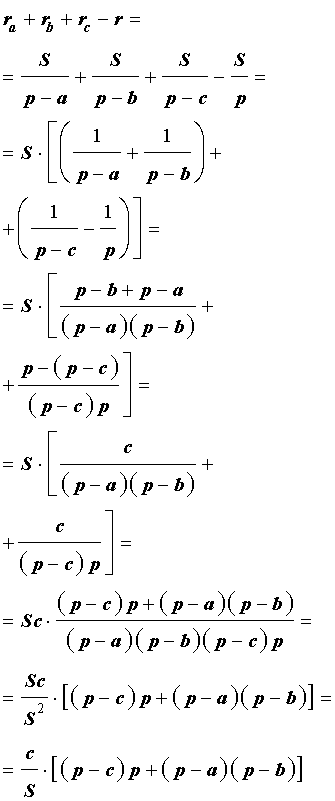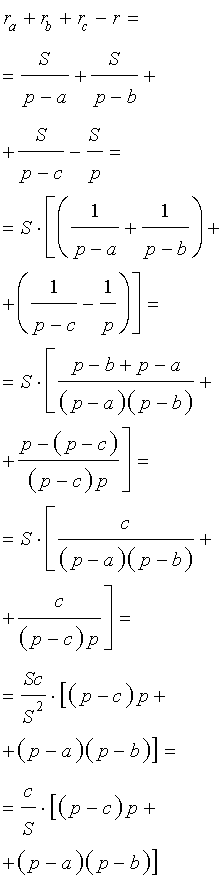Теорема 1 . В любом треугольнике биссектрисы двух внешних углов и биссектриса внутреннего угла, не смежного с ними, пересекаются в одной точке.
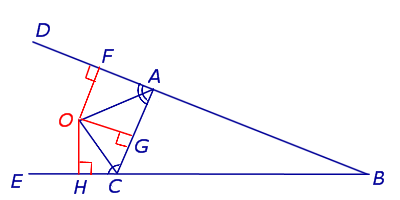
Доказательство . Рассмотрим произвольный треугольник ABC и продолжим, например, стороны BA и BC за точки A и C соответственно (рис.1).
Проведём биссектрисы углов DAC и ECA , которые являются внешними углами треугольника ABC . Обозначим точку пересечения этих биссектрис буквой O . Докажем, что точка O лежит на биссектрисе угла ABC , который является внутренним углом треугольника ABC , не смежным с внешними углами DAC и ECA . С этой целью опустим из точки O перпендикуляры OF , OG и OH на прямые AB , AC и BC соответственно. Поскольку AO – биссектриса угла DAC , то справедливо равенство:
Следовательно, справедливо равенство
Замечание 1 . В ходе доказательства теоремы 1 мы установили, что справедливы равенства
откуда вытекает, что точки F , G и H лежат на одной окружности с центром в точке O .
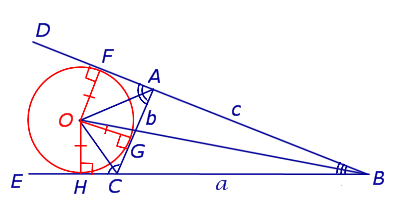
Определение . Окружность называют окружностью, вневписанной в треугольник , или вневписанной окружностью, если она касается касается одной стороны треугольника и продолжений двух других сторон (рис.2).
Замечание 2 . У каждого треугольника существуют три вневписанных окружности. На рисунке 2 изображена одна из них.
Замечание 3 . Центр вневписанной окружности, изображенной на рисунке 2, лежит на биссектрисе угла B , а окружность касается стороны b . Для удобства обозначений и терминологии будем называть эту окружность вневписанной окружностью, касающейся стороны b , и обозначать её радиус символом rb .
Теорема 2 . Пусть вневписанная окружность касается стороны AC треугольника ABC . Тогда отрезки касательных касательных от вершины B до точек касания с вневписанной окружностью равны полупериметру треугольника.
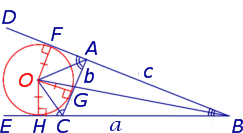
Доказательство . Снова рассмотрим рисунок 2 и докажем, что выполнено равенство
где a, b, c – стороны треугольника ABC . Действительно, отрезки AG и AF равны, как отрезки касательных к окружности, выходящих из точки A . Отрезки CG и CH равны, как отрезки касательных к окружности, выходящих из точки C . Отрезки BF и BH равны, как отрезки касательных к окружности, выходящих из точки B . Отсюда получаем:
где буквой p обозначен полупериметр треугольника ABC . Теорема 2 доказана.
Теорема 3 . Радиус вневписанной окружности , касающейся стороны b , вычисляется по формуле
где буквой S обозначена площадь треугольника ABC , а буквой p обозначен полупериметр треугольника ABC .
Доказательство . Снова рассмотрим рисунок 2 и заметим, что выполнены равенства
Следовательно, справедливо равенство
что и требовалось доказать.
Следствие . Радиусы двух других вневписанных в треугольник ABC окружностей вычисляются по формулам:
Теорема 4 . Если обозначить буквой r радиус вписанной в треугольник ABC окружности, то будет справедлива формула:
Складывая эти формулы и воспользовавшись формулой для радиуса вписанной окружности

что и требовалось доказать.
Теорема 5 . Площадь треугольника можно вычислить по формуле
Доказательство . Перемножим формулы
что и требовалось доказать.
Теорема 6 . Если обозначить буквой R радиус описанной около треугольника ABC окружности, то будет справедлива формула:
Доказательство . Воспользовавшись формулами для радиусов вписанной и вневписанных окружностей, а также формулой Герона, получим
Преобразуем выражение, стоящее в квадратной скобке:
Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Задание 16. Математика ЕГЭ. Вневписанная окружность равнобедренного треугольника касается его боковой стороны.
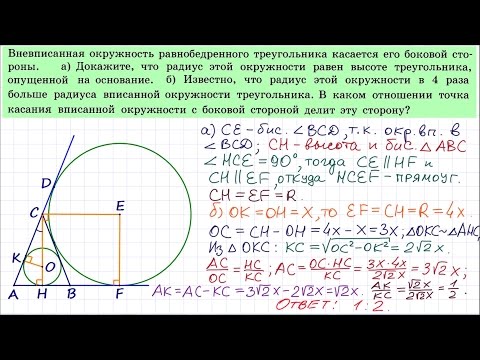
Задание. Вневписанная окружность равнобедренного треугольника касается его боковой стороны.
а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на основание.
б) Известно, что радиус этой окружности в 4 раза больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной окружности с боковой стороной треугольника делит эту сторону?
Решение:
а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на основание.
Вневписанной окружностью называется окружность, которая касается стороны треугольника и продолжений двух других его сторон.
Пусть угол ∠А = ∠С = α, так как треугольника ∆АВС — равнобедренный. Угол ∠DBC – внешний угол треугольника ∆АВС, поэтому ∠DBC = ∠А + ∠С = 2α.
Окружность касается сторон угла ∠DBC, значит, ВО – биссектриса угла ∠DBC, т. е. угол ∠DBО = ∠ОBC = α.
Получаем, что ∠DBО = ∠А = α. Соответственные углы ∠DBО и ∠А при пересечении прямых ВО и АМ секущей AD равны, то прямые ВО и АМ параллельны.
BH – высота треугольника ∆АВС, следовательно, BH перпендикулярна АМ.
АМ – касательная к окружности, следовательно, ОМ перпендикулярна АМ (ОМ – радиус окружности). Значит, ВН параллельна ОМ. Получаем, ВОМН – прямоугольник. Следовательно, радиус окружности равен высоте треугольника, опущенной на основании, т. е. R = BH.
б) Известно, что радиус этой окружности в 4 раза больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной окружности с боковой стороной треугольника делит эту сторону?
Пусть радиус вневписанной окружности ОМ = R, а радиус вписанной в треугольник окружности QK = QH = r. Тогда по условию R = 4r.
Треугольники ∆АВН и ∆QВК – подобные треугольники (∠В – общий, ∠ВКQ = ∠ВНА), следовательно,
QB = BH – QH = 4r – r = 3r
Из прямоугольного треугольника ∆QBK по теореме Пифагора найдем BK:
BK 2 = QB 2 – KQ 2
BK 2 = (3r) 2 – r 2 = 8r 2
AK = 3√2r – 2√2r = √2r
Тогда отношение, в котором точка касания вписанной окружности с боковой стороной треугольника делит эту сторону, равно
Ответ: 1/2
Спасибо! Часто заглядываю на ваш сайт. Как с компьютера, так и с мобильного.. Информация всегда по делу и правдива.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вневписанная окружность треугольника.
Определение.
Окружность, касающаяся стороны треугольника и продолжения двух других его сторон, называется вневписанной окружностью треугольника.
Теорема 1.
Центр окружности, вневписанной в треугольник, есть точка пересечения биссектрис двух внешних и одного внутреннего угла треугольника.
Доказательство.
BF — биссектриса ∠JBG, следовательно F равноудалена от сторон данного угла.
СF — биссектриса ∠JСH, следовательно F равноудалена от сторон данного угла.
Следовательно, точка F равноудалена от сторон ∠BAC.
Таким образом, точка F — центр окружности, касающейся стороны BC и продолжения сторон AB и AC. По определению данная окружность называется вневписанной окружностью треугольника.
Теорема 2.
Отрезок, соединяющий вершину треугольника с точкой касания вневписанной окружности и противолежащей стороны, делит треугольник на два треугольника равного периметра.
Доказательство.
BJ=BG, GC=CH и AJ=AH (свойство отрезков касательных, проведенных из одной точки к окружности).
PΔABC=AB+ BC +AC=AB+ BG + GC +AC=AB+ BJ + AC +CH=AJ+AH.
Так как AJ=AH, то PΔABC/2=AJ=AH и PΔABC/2+AG=AJ+AG=AH+AG=AB+BG+GA=AC+CG+GA.
Следовательно, отрезок AG поделил треугольник ABC на два треугольника равного периметра PΔABC/2+AG.
🌟 Видео
Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Вневписанная окружностьСкачать

7-13. Вневписанная окружность прямоугольного треугольникаСкачать

Сможешь найти радиус вневписанной окружности?Скачать

Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Вневписанная окружностьСкачать
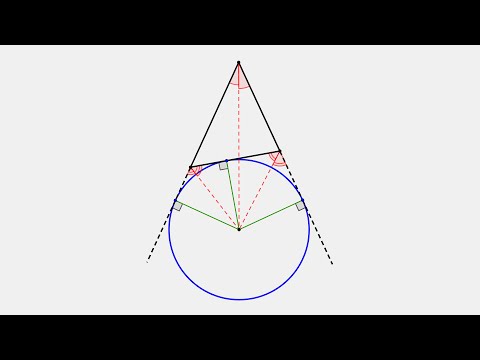
№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Задание 16 ЕГЭ по математике #6Скачать
Построить описанную окружность (Задача 1)Скачать

✓ Как вневписанная окружность Герону помогла | Ботай со мной #083 | Борис ТрушинСкачать

Нахождение радиуса окружности, описанной около равнобедренного треугольника.Скачать

2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Егэ c4. Вневписанная окружностьСкачать

Задание 26 Вневписанная окружностьСкачать

Вневписанная окружность | Теоремы об окружностях - 3Скачать

Задача про две вневписанные окружности | ЕГЭ. Задание 16. Математика | Борис Трушин |Скачать